Следует отметить, что высокая скорость протекания превращения исключает влияние диффузионных процессов во время роста кристаллов. Но на подготовительном (инкубационном) этапе, предшествующем возникновению НВС, роль диффузии компонентов сплава может быть существенной, как это имеет место, например, при бейнитном превращении [4].
Второй сценарий, доказавший свою конструктивность применительно к ОЦК-ГПУ (α - ε) МП на примере титана [5] (как и для ГЦК-ОЦК МП [6]), акцентирует внимание на быстрой плоской деформации типа растяжения - сжатия, инициированной парой волн (ответственных за описание габитусов кристаллов), плоскостей {110}α с достаточно плотной упаковкой атомов и дополнительной перетасовкой деформированных плоскостей. Следует подчеркнуть, что такая перетасовка (а точнее, неоднородный сдвиг) не сказывается на макроскопических морфологических признаках, к которым относятся ориентация габитусной плоскости, межфазные ориентационные соотношения (ОС) и макросдвиг.
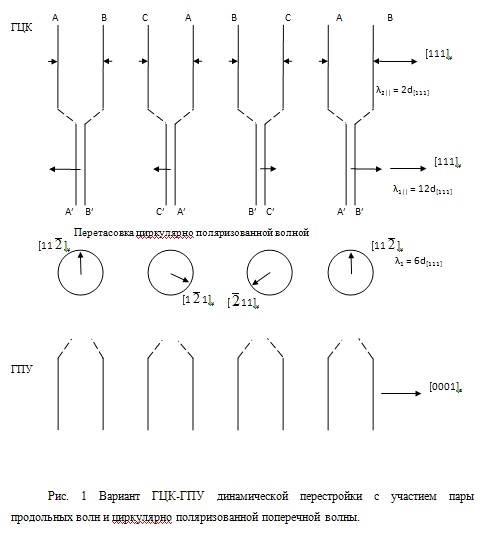
Подчеркнем, сценарий перетасовки плотноупакованных плоскостей может выступать в качестве совершенно независимого третьего сценария для политипных МП, простейшими примерами которых являются ГЦК - ГПУ (γ - ε) [7] и обратное ε - γ превращения. Этот сценарий, связан с согласованным действием продольных и поперечных смещений. Основная идея [7] состоит в том, что перетасовка посредством поперечных смещений пар (или большего числа) плотноупакованных плоскостей (временно обособляемых относительно коротковолновыми продольными смещениями) происходит в те моменты времени, когда вторая система продольных смещений с большими длинами волн обеспечивает увеличение расстояния между соседними обособленными группами плоскостей. Ясно, что в такие моменты времени взаимодействие между подобными группами плоскостей ослаблено. Нелинейное возбуждение решетки такого типа близко к бризерному варианту, и скорость его распространения может быть небольшой, как показывает анализ [8] для возбуждений с чисто продольными смещениями. Третий сценарий МП применительно к ГЦК-ГПУ МП иллюстрирует Рис. 1, взятый из [7].
На рис. 1 представлена пара продольных волн смещений. Одна из них (с наименьшей для направления [111]γ длиной волны λ2║) обеспечивает попарное обособление плотноупакованных плоскостей вида (АВ)-(СА)-(ВС)-(АВ)-..., означающего, что расстояние между плоскостями, заключенными в скобки, меньше расстояния между ближайшими плоскостями, принадлежащими соседним обособленным парам, что снижает сопротивление для попарного перетасовочного сдвига. Вторая продольная волна с длиной волны λ1║=6λ2║ способна в фазе растяжения обеспечить дополнительное увеличение расстояния между обособленными парами, снижая в еще большей степени сопротивление для попарного перетасовочного сдвига пар плоскостей (СА)↑-(ВС)↓, переводящего их в пары (AB)-(AB). В то же время эта волна с максимумами смещений, приходящимися на пары плоскостей (AB), блокирует перетасовку данного типа пар, что и требуется для перестройки ГЦК-ГПУ. Саму перетасовку способна инициировать как линейно поляризованная поперечная волна, так и циркулярно поляризованная волна (на рис. 1 схематически отражено действие именно циркулярной волны). Заметим, что для наглядности величина смещений при попарном обособлении плоскостей явно преувеличена (пары плоскостей, нумеруемые заглавными буквами со штрихами).
К четвертому сценарию МП можно отнести комбинированный вариант, в котором быстро (со сверхзвуковой скоростью) УВП инициирует формирование некоторого промежуточного состояния (ПС) при отношении финальных деформаций, совпадающих с отношением деформаций в пороговом режиме, и последующей эволюцией ПС либо путем релаксации в конечное состояние, либо с помощью нового варианта УВП, как показывает [9], анализ B2-ПС-B19 и B2-B19- B19′ МП в сплавах на основе никелида титана, обладающих эффектом памяти формы. В качестве промежуточного состояния может выступать и вполне определенная фаза, например, В19 в упомянутом выше примере или ε-фаза при обратном α- ε-γ МП в сплавах железа. Заметим, что если второй этап четвертого сценария связан с перетасовкой плоскостей, то макроскопические морфологические признаки не изменяются и, следовательно, задаются динамикой превращения на первом этапе.
Следует подчеркнуть, что для второго сценария МП характерно включение в межфазные ориентационные соотношения именно тех плоскостей исходной фазы, которые испытывают трансформацию в ходе МП, причем эти плоскости перпендикулярны габитусным плоскостям кристалла. Дополнительная особенность может быть связана с трансформацией плоскости, являющейся плоскостью симметрии исходной фазы. Именно для этого случая должна реализоваться строгая параллельность плоскостей, входящих в ОС, тогда как для остальных вариантов характерны разориентировки (пусть и небольшие) подобных плоскостей.
В то же время для первого сценария плоскости, входящие в ОС, образуют с габитусами наименьшие углы, а для третьего сценария (выступающего в качестве самостоятельного) габитусная плоскость совпадает с ориентацией плоскостей, меняющих порядок укладки. Таким образом, имея информацию о наблюдаемых морфологических признаках можно судить о наиболее вероятном динамическом сценарии МП применительно к спонтанному формированию мартенсита (при охлаждении или нагревании).
Отдельный (пятый) сценарий относится к мартенситу деформации, образующемуся на стадии пластического течения материала. Особенности этого МП адекватно описываются в модели кристонных носителей пороговой деформации [10]. Эти носители сдвига возникают при контактном взаимодействии дислокаций с пересекающимися плоскостями скольжения.
Работа выполнена при финансовой поддержке РФФИ (номер проекта 14-08-00734)
Рецензенты:
Потехин Б.А., д.т.н., профессор, заведующий кафедрой технологии металлов ФГБОУ ВПО «Уральский государственный лесотехнический университет», Министерство образования и науки РФ, г.Екатеринбург;
Пугачева Н.Б., д.т.н., доцент, ведущий научный сотрудник Федерального государственного бюджетного учреждения науки Институт машиноведения Уральского отделения Российской академии наук (ИМАШ УрО РАН), Министерство образования и науки РФ, г.Екатеринбург.



