Законы распространения электромагнитных волн в свободном пространстве сравнительно просты, но чаще всего радиотехника имеет дело не со свободным пространством, а с распространением электромагнитных волн над земной поверхностью. Как показывает и опыт и теория, поверхность Земли сильно влияет на распространение электромагнитных волн, причем сказываются как физические свойства поверхности (например, различия между свойствами атмосферы над морем и сушей), так и ее геометрическая форма (общая кривизна поверхности земного шара и отдельные неровности рельефа). Влияние это различно для волн разной длины и для разных расстояний между передатчиком и приемником [7].
Состав атмосферы Земли представляет собой смесь взаимодействующих друг с другом компонентов. Соотношения между концентрацией этих компонентов постоянно меняется, что приводит к разнообразию ситуаций. Основные особенности структуры атмосферы отражены в ее послойном делении. Атмосфера представляется состоящей из концентрических сферических оболочек с различными физическими свойствами [4,6,7].
В реальной атмосфере вследствие изменений температуры, давления и влажности происходят сложные пространственно–временные изменения показателя преломления. Различают сезонные и суточные изменения показателя преломления в атмосфере, а также случайные изменения, обусловленные атмосферной турбулентностью. Сезонные изменения обусловлены, главным образом, годовым ходом влажности с максимумом в теплое полугодие. Наибольшие изменения показателя преломления имеют место в нижнем слое атмосферы, что обусловлено большими изменениями в этом слое температуры и влажности. Суточные изменения показателя преломления атмосферы наиболее значительны у слоя атмосферы расположенного у земной поверхности [1-5].
Они также обусловлены значительной амплитудой суточного хода метеорологических величин - температуры и влажности воздуха. Количественной мерой таких изменений в пространстве служит градиенты этих величин [6, 8].
В практике обычно учитывают изменения показателя преломления атмосферы только по высоте, пренебрегая горизонтальной изменчивостью [1,3-5].
Цель работы – рассмотрение влияния горизонтального градиента показателя преломления на горизонтальную траекторию оптического сигнала.
Материалы исследований. Известно, что под градиентом (gradf) величины f понимают вектор, который по направлению совпадает с нормалью N к эквискалярной поверхности, а по модулю равен производной от f по Nс обратным знаком [8]:
![]() (1)
(1)
Наибольший практический интерес представляют горизонтальная и вертикальная проекция gradf:
![]() (2)
(2)
где n – нормаль к изолиниям величины f на уровенной поверхности (в частности к изобарам или изотермам).
На практике при расчете градиентов истинные производные от метеорологических величин заменят отношением конечных разностей, т. е полагают
![]()
Из курса физики известно, что при прохождении оптического сигнала границы раздела двух сред с различными значениями показателя преломления наблюдается отклонение траектории от прямолинейной [10].
С практической точки зрения представляется интересным рассмотрение влияния горизонтальных градиентов метеорологических величин на траекторию горизонтального оптического сигнала в условиях градиентной атмосферы. Неоднородности гидрометеорологических параметров атмосферы, обусловленные неоднородностью земной поверхности, вызывают изменения преломляющих свойств атмосферы.
В качестве комплексной характеристики атмосферы в исследовании был использован показатель преломления атмосферы, расчёт которого осуществляется по известному соотношению:
![]() (3)
(3)
где T–температура воздуха (К), е – парциальное давление водяного пара (г/м3), р–атмосферное давление (мб) [6, 8].
Представим атмосферу как совокупность слоев с различными значениями показателя преломления (n0, n1, ….ni), расположенными перпендикулярно земной поверхности (плоскость XOY), причем n0 <ni. В данной постановке задачи структура атмосферы графически может быть представлена как на рис.1.
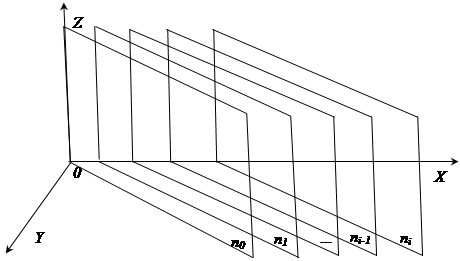
Рис. 1. Структура атмосферы
Пусть оптический сигнал распространяется относительно земной поверхности горизонтально в направлении ОА под углом x0 к границе раздела двух соседних слоев с показателями преломления n0 и n1 соответственно, рис. 2.

Рис.2.Траектория оптического сигнала
Тогда на границе раздела соседних слоев выполняется известное соотношение:
![]() (4)
(4)
где n0, n1 – показатели преломления на границе раздела соседних слоев; x0, x1 – угол падения и преломленный угол зондирующего оптического сигнала относительно нормали на границе раздела двух соседних слоев с показателями преломления n0 и n1 соответственно [10].
Продифференцируем (4) по y, получим
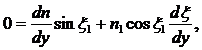
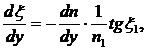 (5)
(5)
Так как
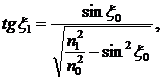
![]()
![]() (6)
(6)
Преобразуем (5) используя (6) к следующему виду:
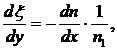
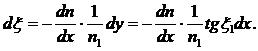 (7)
(7)
Поскольку угол рефракции α определяется, как ![]() то выражение для определения величины угла рефракции можно записать в следующем виде:
то выражение для определения величины угла рефракции можно записать в следующем виде:
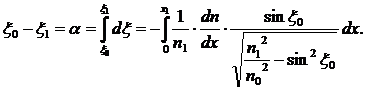
Величину преломленного угла x1можно определить как:
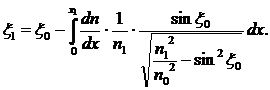 (8)
(8)
Определим АВ – величину отклонения траектории оптического сигнала в направлении ОА (см. рис.2).Так как dx = АВ и из (4)![]() то окончательно можем получить:
то окончательно можем получить:
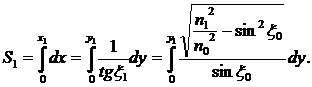 (9)
(9)
Полученное выражение позволяет произвести расчет отклонения траектории оптического сигнала от прямолинейной при распространении последнего в направлении ОА (см. рис.2).
Проведя дальнейшие преобразования полученных выражений (8) и (9) в общем виде будем иметь:
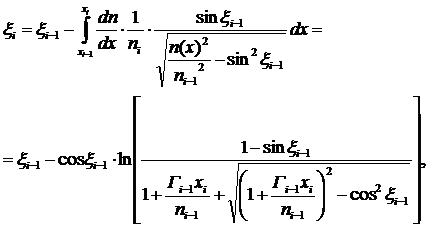 (10)
(10)
где ![]() –горизонтальный градиент показателя преломления.
–горизонтальный градиент показателя преломления.
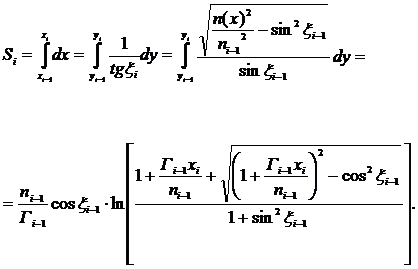 (11)
(11)
Заключение. Полученные выражения (10) и (11) позволяют решать практические задачи, где имеет место прохождение горизонтального оптического сигнала в слое градиентной атмосферы. Учет горизонтального градиента показателя преломления атмосферы позволит рассчитать величину возможных ошибок, вызванных отклонениями траектории оптического сигнала (рис.2) от прямолинейной.
Рецензенты:
Душин А.В., д.т.н., доцент, начальник кафедры управления и информационно-технического обеспечения, ФКОУ ВПО «Воронежский институт ФСИН России», г. Воронеж;
Ирхин В.П., д.т.н., доцент, профессор кафедры основ радиотехники, ФКОУ ВПО «Воронежский институт ФСИН России», г. Воронеж.



