Для исследования коллекторских характеристик призабойной зоны пластов используются различные гидродинамические, геофизические, термогидродинамические методы. В работе для оценки коллекторских характеристик пористой среды, окружающей полость формы трещины, используется метод опрессовки. Метод заключается в следующем: в полости, частично содержащей жидкость и частично газ, резко повышается давление за счет дополнительного введения газа. Далее исследуется динамика релаксации давления за счет фильтрации жидкости в окружающую пористую среду. Темп релаксации давления зависит от коллекторских характеристик окружающей пористой породы. Поэтому по времени релаксации давления можно судить, например, о величине коэффициента проницаемости породы вокруг полости.
В [10; 14] метод опрессовки используется для оценки коллекторских характеристик пористой среды, насыщенной газом. Использование волн давления с целью нагрева и очистки призабойной зоны, а также исследование нефтяных скважин рассмотрено в [4; 6-8; 16]. Процесс распространения импульса давления в пористой среде, насыщенной газом, исследуется в [2; 9; 11; 12]. Колебательные процессы, происходящие в неньютоновских жидкостях, исследуются в [1; 5; 15].
В данной работе исследуется динамика релаксации давления в полости, окруженной насыщенной жидкостью пористой и проницаемой средой после ее опрессовки. Получено нелинейное интегральное уравнение, описывающее релаксацию давления в полости. На его основе получены численные решения и проведен анализ зависимости времени релаксации давления в полости от коллекторских характеристик окружающей пористой породы, а также от начального объемного содержания газа.
1. Основные уравнения. Пусть в исходном состоянии (t < 0) давление жидкости во всем пористом пласте вокруг полости постоянно и равно 
, а сама полость частично заполнена жидкостью и частично газом (рис. 1). В момент времени t = 0 давление в полости мгновенно увеличивается до значения 
, например, введением некоторого количества газа. Далее, за счет фильтрации жидкости в окружающее пористое пространство, давление в полости будет снижаться до значения .
При описании этих процессов примем следующие допущения: внутри полости давление однородно, фазовые переходы и фильтрация газа через боковые поверхности полости отсутствуют, т.е. масса газа внутри полости остается постоянной в течение всего процесса. Стенки полости (трещины) плоскопараллельны, и расстояние между ними намного меньше, чем линейные размеры стенок. Фильтрация жидкости происходит только через переднюю стенку, а остальные части поверхности полости непроницаемы. Предполагается, что газовая фаза в полости находится в специальном контейнере, который исключает ее попадание в окружающую полость пористую среду. Газовая фаза будет работать как объемная «пружина», выталкивающая содержащуюся в ней жидкость в окружающее пористое пространство.
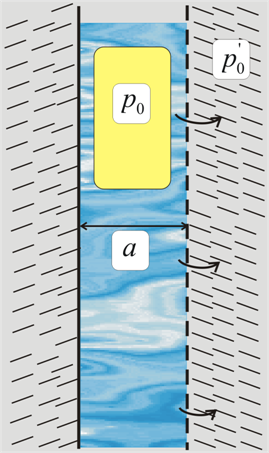
Рис. 1. Схематическое изображение полости, окруженной насыщенной жидкостью пористой средой.
В рамках вышеизложенных допущений уравнение сохранения массы жидкости внутри полости запишем в виде [3; 13]:
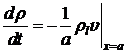, (1)
где 
– средняя плотность жидкости внутри полости, которая определяется по формуле 
; 
– плотность жидкости; 
– объемная доля газа в полости; 
– полутолщина полости с плоскопараллельными стенками; 
– скорость фильтрации жидкости через стенки полости.
Для определения скорости фильтрации жидкости из полости в окружающую пористую среду используем закон Дарси:
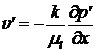, (2)
где 
– динамический коэффициент вязкости жидкости; 
– коэффициент проницаемости; 
– давление и скорость фильтрации жидкости вокруг полости.
Поле давления вокруг полости описывается с помощью уравнения пьезопроводности:
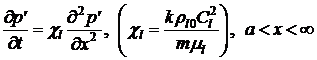. (3)
Здесь 
– коэффициент пьезопроводности; 
– коэффициент пористости; 
– скорость звука в жидкости.
Сжимаемость жидкости, находящейся в полости и в пористой среде, будем учитывать в акустическом приближении:
. (4)
Газ будем считать калорически совершенным, тогда для его поведения примем политропический закон:
, (5)
где 
– показатель политропы, 
– начальное давление в полости. Здесь и далее индекс (0) внизу соответствует начальному значению величины.
Начальное условие для уравнения (3) запишем в виде:
. (6)
Граничные условия на стенке полости (r = a) для уравнений (2), (3) могут быть записаны в виде:
. (7)
После несложных преобразований получаем следующее интегральное уравнение, описывающее релаксацию давления в полости:
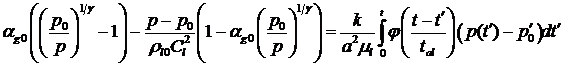, (8)
где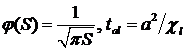 
.
2. Результаты численных расчетов. Уравнение (8) решается численным методом. В работе для изучения динамики релаксации давления в полости предлагается использовать период полувосстановления давления. Периодом полувосстановления давления будем называть промежуток времени, в течение которого разница между значениями давлений в полости и пористой среде снижается в два раза от начальной разницы.
На рис. 2 представлены результаты численных расчетов, иллюстрирующие процесс релаксации давления в полости при различных значениях пористости. Для начального объемного содержания газа во всех вариантах принято значение 
, начальный перепад давления в полости равен 
. Период полувосстановления давления при 
равен 
, а при 
– 
. Увеличение пористости в два раза приводит к уменьшению периода полувосстановления давления также в два раза, т.е. период полувосстановления давления обратно пропорционален пористости.
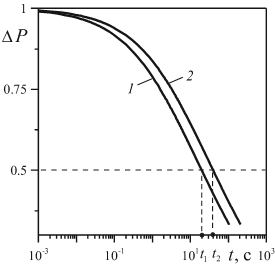
Рис. 2. Эволюция давления в полости с плоскопараллельными стенками при различных значениях коэффициента пористости : 1 – 
; 2 –
.
На рис. 3 представлены зависимости периода полувосстановления давления 
от начального объемного содержания газа при различных значениях коэффициента проницаемости . Анализ графиков показывает, что зависимость периода полувосстановления давления от начального объемного содержания газа квадратичная, т.е. 
.
Также исследования показали, что период полувосстановления давления имеет обратную зависимость от коэффициента проницаемости пористой среды и прямую квадратичную зависимость от полутолщины полости.
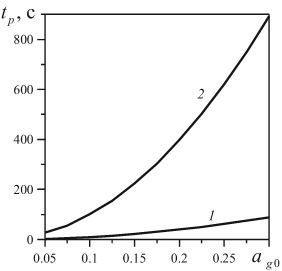
Рис. 3. Зависимости периода полувосстановления давления от начальной объемной доли газа в полости при различных значениях коэффициента проницаемости : 1 – 
, 2 – 
.
Выводы. Разработана математическая модель и получено нелинейное интегральное уравнение, описывающее процесс релаксации давления в полости формы трещины, окруженной насыщенной жидкостью пористой средой и опрессованной введением газа. В результате численного анализа интегрального уравнения установлено: зависимость периода полувосстановления от коэффициентов проницаемости и пористости является обратно пропорциональной, а от начального объемного содержания газа является прямой квадратичной.
Полученные результаты могут быть использованы при определении метода исследования коллекторских характеристик призабойной зоны нефтяных скважин.
Работа выполнена при поддержке гранта СФ БашГУ № В14-19.
Рецензенты:
Мустафина С.А., д.ф.-м.н., профессор кафедры математического моделирования, Стерлитамакский филиал ФГБОУ ВПО «Башкирский государственный университет», Республика Башкортостан, г. Стерлитамак;
Михайлов П.Н., д.ф.-м.н., профессор кафедры алгебры, геометрии и методики обучения математике, Стерлитамакский филиал ФГБОУ ВПО «Башкирский государственный университет», Республика Башкортостан, г. Стерлитамак.