Практическое применение технологии «классического» MPC к сложным объектам химической технологии, особенно к используемым в процессах синтеза, затруднительно ввиду:
-
нелинейности уравнений математического описания в используемых моделях и, как следствие, наличие проблем их сходимости при решении задачи оптимизации на каждом шаге прогноза;
-
наличия неизмеряемых возмущений;
-
наличия помех в контурах управления и измерения;
-
невозможности измерения вектора состояния объекта;
-
необходимости учета ограничений на управляющие и управляемые переменные и, как следствие, невозможности быстрого и аналитического решения задачи минимизации квадратичного функционала качества управления;
-
необходимости быстрого расчета прогноза.
Целью данной статьи является применение одной из промышленных реализаций управления на основе прогнозирующих моделей к строгой нелинейной модели динамики объекта при использовании для прогнозирования дискретной линейной стационарной модели пространства состояний.
В качестве инструмента исследования в статье используется пакет MPC Toolbox системы компьютерной математики MATLAB/ Simulink.Подробное описание моделей, используемых MPC Toolbox при оценке и прогнозе состояния, а также наблюдателя состояния приведено в работе [2].
Описание объекта управления
В качестве объекта управления MPC-регулятора используется строгая нелинейная модель динамических режимов ХТС секции синтеза аммиака [5], построенная в программном пакете Aspen Dynamics. Модель является упрощенной реализацией схемы технологического процесса Kellogg с трехполочной колонной синтеза без вторичного аммиачного сепаратора (т.к. содержание аммиака в синтез-газе постоянно и не превышает 5%)[1]. Каждый слой катализатора (полка) моделируется блоком адиабатического реактора идеального вытеснения (модель RPlug).Модель представляет собой систему дискретизированных по пространству обыкновенных дифференциальных уравнений материального и теплового баланса, полученных по методу конечных разностей.
Скорость химической реакции в данной модели рассчитывалась помощью специального программного модуля, разработанного авторами и реализующего различные известные кинетические закономерности процесса синтеза аммиака на промотированных железных катализаторах. При расчетах данной модели использовалось модифицированное уравнение Темкина-Пыжева в терминах активностей[3]:
![]() , (1)
, (1)
где:
![]() ,
, ![]() ,
, ![]() – активности (фугитивности) соответствующих компонентов реакции, атм,
– активности (фугитивности) соответствующих компонентов реакции, атм,
![]() – константа скорости реакции,
– константа скорости реакции,
![]() – коэффициент активности катализатора,
– коэффициент активности катализатора,
![]()
– константа равновесия,
![]() – коэффициент диффузионного торможения, рассчитываемый по эмпирическому кубическому уравнению:
– коэффициент диффузионного торможения, рассчитываемый по эмпирическому кубическому уравнению:
![]() , (2)
, (2)
коэффициенты ![]() которого получаются интерполированием таблицы, приведенной в [Dyson], при заданном давлении системы.
которого получаются интерполированием таблицы, приведенной в [Dyson], при заданном давлении системы.
Блок-схема объекта управления - модели ХТС секции синтеза в Aspen Dynamics - представлена на рисунке 1.
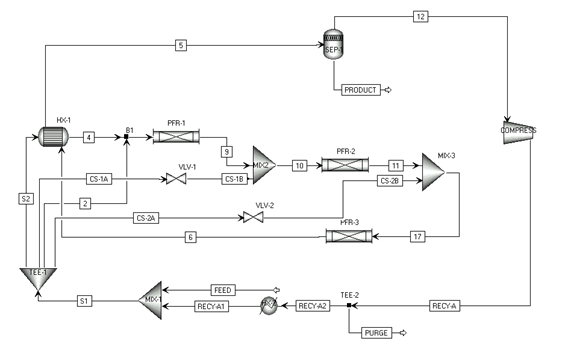
Рис.1.Схема объекта управления MPC-регулятора
Идентификация модели объекта пространства состояний
Матрицы пространства состояний ![]() ,
, ![]() ,
, ![]() и
и ![]() были получены путем линеаризации системы нелинейных уравнений динамики объекта:
были получены путем линеаризации системы нелинейных уравнений динамики объекта:
![]() (3)
(3)
при некоторых номинальных значениях ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Тогда процесс линеаризации может быть представлен в следующем виде:
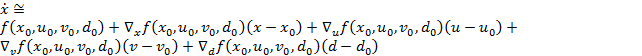 (4)
(4)
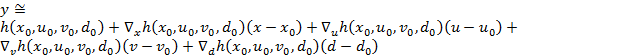 ,
,
где матрицы пространства состояний получаются из матриц Якоби вышеприведенных уравнений.
Идентификация модели осуществлялась в стационарном режиме функционирования ХТС. Была использована встроенная функция пакета Aspen Dynamics – Control Design Interface (CDI). В результате была получена непрерывная линейная стационарная модель вида:
![]() , (5)
, (5)
которая впоследствии дискретизировалась во времени с использованием известных закономерностей. Матрицы пространства состояний ![]() ,
, ![]() ,
, ![]() и
и![]() были получены с помощью подпрограммы-макроса для CDI. Расчет осуществляется путем исключения из исходной динамической модели всех алгебраических переменных, которые не были включены в линеаризованную модель.
были получены с помощью подпрограммы-макроса для CDI. Расчет осуществляется путем исключения из исходной динамической модели всех алгебраических переменных, которые не были включены в линеаризованную модель.
Полученная модель включает 192 переменные состояния, 4 управляющие переменные и 4 переменные выхода:
-
Матрица
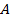 содержит 20029 ненулевых элементов.
содержит 20029 ненулевых элементов.
-
Матрица
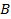 содержит 566 ненулевых элементов.
содержит 566 ненулевых элементов.
-
Матрица
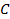 содержит 24 ненулевых элемента.
содержит 24 ненулевых элемента.
-
Матрица
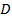 является нулевой, т.к. принимается, что система не имеет явной прямой связи.
является нулевой, т.к. принимается, что система не имеет явной прямой связи.
Индекс Нидерлински [4] равен 0,092529 (> 0), что говорит о том, что замкнутая MIMO-система может быть устойчивой.
Описание переменных – компонент векторов выхода и управления –представлено в таблицах 1 и 2.Для корректной приоритизации переменных объекта при их использовании в процессе минимизации квадратичного критерия качества управления, было выполнено их масштабирование. Номинальному значению переменной сопоставлялось значение 50%.
Таблица 1
Вектор выходных переменных объекта (измерений)
|
№ п/п |
Обозначение |
Описание |
Номинальное значение в единицах измерения |
Номинальное значение в % |
|
1 |
|
Температура газа на выходе с I полки колонны синтеза, °С |
466,4 |
50 |
|
2 |
|
Температура газа на выходе со II полки колонны синтеза, °С |
495,4 |
50 |
|
3 |
|
Температура газа на выходе с III полки колонны синтеза, °С |
490,0 |
50 |
|
4 |
|
Содержание инертной примеси (метана) в циркуляционном газе, мольные доли |
0,048 |
50 |
Таблица 2
Вектор управляющих переменных объекта
|
№ п/п |
Обозначение |
Описание |
Номинальное значение |
Номинальное значение в % |
|
1 |
|
Относительный расход холодного байпаса на I полку колонны синтеза |
0,23 |
50 |
|
2 |
|
Относительный расход холодного байпаса на II полку колонны синтеза |
0,14 |
50 |
|
3 |
|
Относительный расход холодного байпаса на III колонны синтеза |
0,13 |
50 |
|
4 |
|
Положение заслонки делителя потока отдувочного газа |
0,03 |
50 |
Принципиальная схема системы управления
В предлагаемой схеме управления температуры на выходе из каждой полки управляются путем изменения положения заслонок делителя потоков холодных байпасов, подаваемых перед соответствующей полкой. Также необходимо ограничивать содержание инертных примесей в циркуляционном газе на требуемом уровне, что обеспечивается изменением положения заслонки делителя продувочного газа (изменением его относительного расхода).
В данной работе не учитываются нелинейности, вносимые характеристиками вентилей, используемых для дросселирования потоков, подаваемых в колонну синтеза по линиям холодных байпасов, т.к. подразумевается, что MPC-регулятор управляет заданием регуляторов более низкого уровня, что является общепринятой практикой в промышленности. В качестве регуляторов низкого уровня предлагается использовать робастные регуляторы первого порядка, синтез которых не является темой данного исследования.
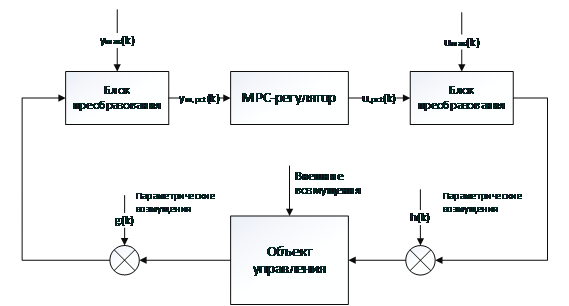
Рис.2.Структурная схема системы управления
Для решения задачи прогнозирующего управления использована схема управления, структура которой представлена на рисунке 2. Масштабирование векторов состояния и управления объекта осуществляется в режиме реального времени в блоках преобразования, входными параметрами которых являются векторы максимальных значений соответствующих переменных. Предложенная схема предусматривает возможность проверки работоспособности системы управления на предмет отработки различных параметрических возмущений.
Для реализации данной схемы управления использовался пакет Simulink. В качестве модуля сопряжения Simulinkс Aspen Dynamics использовался специальный блок AMSimulink, входящий в комплект поставки AspenDynamics.
Переходные характеристики процесса регулирования
Результаты работы системы управления при отработке ступенчатого возмущения по всем каналам управления в момент времени ![]() представлены на рисунке 3.
представлены на рисунке 3.
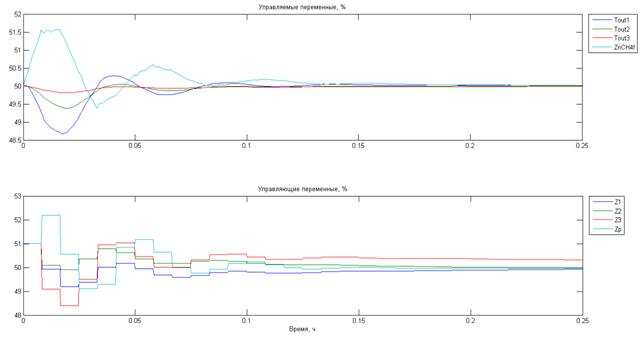
Рис.3. Переходная характеристика процесса, вызванная ступенчатым воздействием по всем каналам управления (время дискретизации 5 с)
Быстродействие MPC-регулятора может быть достигнуто за счет увеличения коэффициентов модели неизмеряемых возмущений. Результаты увеличения коэффициента усиления наблюдателя состояния в 32 раза от номинального представлены на рисунке 4.
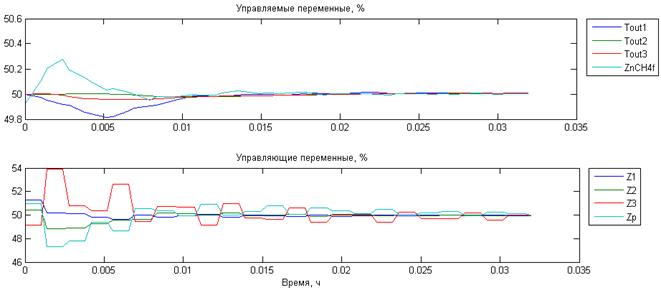
Рис.4. Переходная характеристика процесса, вызванная ступенчатым воздействием по всем каналам управления (время дискретизации 3 с)
Выводы
-
Компьютерная модель секции синтеза в Aspen Dynamics совместно с модулем расчета кинетики позволили получить линеаризованную модель объекта в пространстве состояний.
-
Линеаризованная модель пространства состояний была использована при синтезе многопараметрической (MIMO) системы MPC-управления температурным режимом колонны синтеза, а также содержанием инертных примесей в циркуляционном газе.
-
Предложенная система управления показала работоспособность в условиях параметрических возмущений по всем каналам управления, а также при наличии внешних возмущений.
Рецензенты:
Мусаев А.А., д.т.н., профессор, декан факультета информационных технологий и управления ФГБОУ ВПО «Санкт-Петербургский государственный технологический институт (технический университет)», г. Санкт-Петербург;
Харазов В.Г., д.т.н., профессор, профессор кафедры автоматизации процессов химической промышленности ФГБОУ ВПО «Санкт-Петербургский государственный технологический институт (технический университет)», г. Санкт-Петербург.



