Известно [1], что структура литого изделия во многом зависит от характера протекания процесса затвердевания, когда закладываются основные физико-химические свойства отливки. Формирование макроструктуры отливки определяется технологическими режимами заливки и охлаждения расплава в форме, а также конструктивными особенностями изделия (конусность, отношение высоты отливки к диаметру). Поскольку экспериментальное исследование процессов затвердевания отливок трудозатратно и дорогостояще, широкое распространение получили методы математического моделирования, ориентированные на привлечение современной вычислительной техники и численных методов [2–8].
В работах [4–5] изучена конвекция в жидком расплаве металла и макросегрегация при образовании литой структуры. Модель, основанная на кристаллизации многокомпонентного сплава с учетом конвекции, предполагает совместное решение уравнений, описывающих процессы тепло-массопереноса в твердой, твердожидкой и жидкой фазах. Результаты оптимизации конструкции изложницы при изготовлении массивных отливок и слитков представлены в [7,8]. Исследованию влияния свободной конвекции на температурные поля в расплаве и качество литой структуры при затвердевании (кристаллизации) крупного слитка массой 142 т посвящена работа [9]. Имеются варианты [10] учета связанности тепловых и гидродинамических полей с учетом турбулентных режимов течения расплава.
В данной работе исследуются процессы заливки и кристаллизации при изготовлении превентора. Превентор – это ответственный рабочий элемент комплекта противовыбросового оборудования [12], устанавливаемый на устье нефте- и газодобывающей скважины.
Математическая постановка задачи
Процесс производства отливки превентора можно условно разделить на два этапа: разливку и затвердевание расплава. На первом этапе жидкую сталь из ковша разливают в заранее заготовленные формы (рис.1). Форма состоит из стального остова, представляющего собой параллелепипед с отсутствующими передней и задней гранями, и формы из альфасет-смеси. Вторая стадия получения отливки – затвердевание жидкого металла в форме. На этой стадии важно получить однородный по химическому составу, механическим и физическим свойствам, а также не содержащий значительных дефектов металл. Характерные размеры отливки: нижний диаметр 480 мм, верхний диаметр 760 мм, высота детали 1254 мм.
Формирование структуры происходит в двухфазной зоне, представляющей собой гетерогенную область из растущих кристаллов с окружающим расплавом. Средний размер кристаллов прямо пропорционален ширине этой зоны, которая, в свою очередь, обратно пропорциональна отводимому потоку тепла. Теплофизические явления, происходящие в двухфазной зоне, включают взаимосвязанные процессы тепломассопереноса, фильтрацию расплава в междендритном пространстве, формирование растущих кристаллов [13].
а 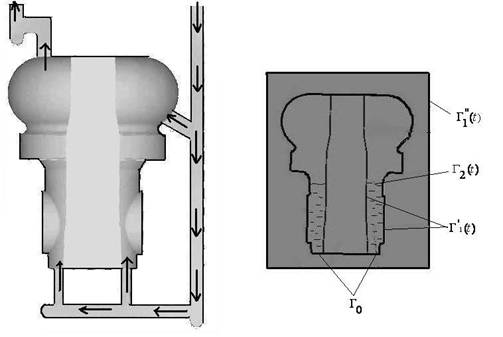 б
б
Рис. 1. Форма для заливки превентора; а – схема движения расплава металла по форме, б – схема расчетной области – фронтальный разрез
Для описания процессов теплообмена используется однофазный подход – уравнения сохранения энергии записываются для всей области в целом, содержащей как жидкий расплав, так и затвердевший металл. В этом случае нет необходимости явным образом отслеживать положение границы ![]() фазового перехода, ее положение определяется апостериорно по изолиниям температур солидус и ликвидус.
фазового перехода, ее положение определяется апостериорно по изолиниям температур солидус и ликвидус.
В однофазном подходе предполагается, что существует простое соотношение, устанавливающее функциональную зависимость количества твердой фазы от температуры.
Предположим, что теплота кристаллизации выделяется внутри интервала кристаллизации, ограниченного равновесными значениями температур ликвидуса и солидуса, соответствующими исходному содержанию растворимой примеси в расплаве, а скорость кристаллизации находится из равновесной диаграммы состояния расплава.
Дифференциальное уравнение, описывающее теплообмен в исследуемой области, имеет вид:
![]() (1)
(1)
где ![]() ,
, ![]() – плотность и коэффициент теплопроводности, в общем случае зависящие от температуры,
– плотность и коэффициент теплопроводности, в общем случае зависящие от температуры, 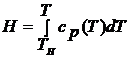 – энтальпия,
– энтальпия, ![]() – удельная теплоемкость, изменение которой в диапазоне
– удельная теплоемкость, изменение которой в диапазоне ![]() отражает эффект тепловыделения при кристаллизации,
отражает эффект тепловыделения при кристаллизации, ![]() – вектор скорости в двухфазной области,
– вектор скорости в двухфазной области, ![]() – вектор скорости жидкой фазы,
– вектор скорости жидкой фазы, ![]() – относительное объемное содержание жидкой фазы.
– относительное объемное содержание жидкой фазы.
Твердая фаза считается неподвижной, а значит, в конвекции принимает участие только доля объема, занятого жидкостью, при этом под скоростью среды понимается «доля скорости», вносимая жидкой фазой ![]() .
.
Уравнение (1) описывает перенос тепла в жидкой фазе как за счет конвекции, так и механизмами теплопроводности.
Поля скоростей и давлений в расплаве и двухфазной зоне определяются уравнением движения, которое с учетом несжимаемости потока и закона Дарси, принимает вид:
![]() (2)
(2)
где ![]() – давление,
– давление,![]() – сдвиговая вязкость,
– сдвиговая вязкость, ![]() – турбулентная вязкость.
– турбулентная вязкость.
Для определения проницаемости ![]() в двухфазной зоне используется соотношение Козени – Кармана [14]:
в двухфазной зоне используется соотношение Козени – Кармана [14]:
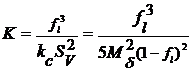
где ![]() – удельная поверхность твердой фазы (на единицу объема),
– удельная поверхность твердой фазы (на единицу объема), ![]() – постоянная Козени – Кармана, которая принимает различные значения в зависимости от характеристик пористой среды,
– постоянная Козени – Кармана, которая принимает различные значения в зависимости от характеристик пористой среды, ![]() – отношение площади поверхности к объему для твердой фазы,
– отношение площади поверхности к объему для твердой фазы, ![]() – параметр формы.
– параметр формы.
Граничные условия
1) Скорость расплава на входе в форму (![]() ) подчиняется логарифмическому закону распределения. На границе перехода от твердо-жидкой к абсолютно твердой фазе
) подчиняется логарифмическому закону распределения. На границе перехода от твердо-жидкой к абсолютно твердой фазе ![]() скорость
скорость ![]() автоматически становится равной 0, поскольку
автоматически становится равной 0, поскольку ![]() , а
, а ![]() на
на ![]() . На внутренних твердых стенках
. На внутренних твердых стенках ![]() задано условие прилипания
задано условие прилипания ![]() .
.
2) ![]() на
на ![]() – условие равенства нормальных напряжений давлению газа
– условие равенства нормальных напряжений давлению газа ![]() над свободной поверхностью. Кривизной свободной поверхности расплава пренебрегаем.
над свободной поверхностью. Кривизной свободной поверхности расплава пренебрегаем.
3) Уравнение свободной поверхности расплава имеет вид: ![]() ,
,
тогда ![]() на
на ![]() -
-
в эйлеровой форме условие продвижения свободной поверхности во времени и пространстве (используется для нахождения формы свободной поверхности).
4) ![]() на
на ![]() – условия стыковки на границе отливки и формы, где
– условия стыковки на границе отливки и формы, где ![]() – нормаль к поверхности,
– нормаль к поверхности, ![]() – температура отливки,
– температура отливки, ![]() – температура формы,
– температура формы, ![]() – коэффициент теплообмена между отливкой и формой.
– коэффициент теплообмена между отливкой и формой.
5) ![]() на
на ![]() – условия на свободной поверхности расплава с учетом лучистого и конвективного теплообмена, где
– условия на свободной поверхности расплава с учетом лучистого и конвективного теплообмена, где ![]() – постоянная Стефана – Больцмана,
– постоянная Стефана – Больцмана, ![]() – степень черноты материала отливки,
– степень черноты материала отливки, ![]() – коэффициент теплообмена между расплавом и внутренностью формы,
– коэффициент теплообмена между расплавом и внутренностью формы, ![]() – температура во внутренней полости формы, не заполненной расплавом.
– температура во внутренней полости формы, не заполненной расплавом.
6) ![]() на
на ![]() – условие на свободной поверхности формы и окружающей среды, где
– условие на свободной поверхности формы и окружающей среды, где ![]() – коэффициент теплообмена.
– коэффициент теплообмена.
Начальные условия
1) Предполагается, что в начальный момент времени свободная поверхность, совпадающая с ![]() , является плоской и известно начальное распределение скоростей на ней.
, является плоской и известно начальное распределение скоростей на ней.
2) В начальный момент времени температура расплава ![]() °С, температура окружающей среды 20 °С, температура формы
°С, температура окружающей среды 20 °С, температура формы ![]() °С.
°С.
Численная реализация задачи
Линеаризация и численное решение полученной системы уравнений в полной нестационарной трехмерной постановке выполнено средствами программного кода ProCAST. Конечно-элементная модель включает в себя около 1 181 тысяч элементов.
Изначально было проведено моделирование двух процессов: заливки стали в течение 35 секунд и последующая кристаллизация. Данные процессы рассматривались как единая задача. Далее был проведен расчет только процесса кристаллизации, начальные условия по температуре для которого задавались константами в ProCAST. Проведенный анализ результатов показал, что учет конвекции расплава при заливке не вносит существенных изменений в результаты расчета процесса кристаллизации, поэтому в дальнейшем исследовалось только затвердевание слитка без описания этапа заливки.
![]()
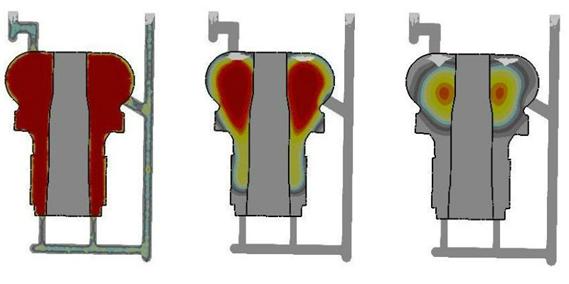
Рис. 2. Кристаллизация превентора из стали марки 42CrMoV:
(а) относительная доля твердого вещества по окончании процесса заливки, (б) – через 27 мин после окончания заливки, (в) - через 95 мин после окончания заливки (0 – жидкий металл, 1 – затвердевший металл)
![]()
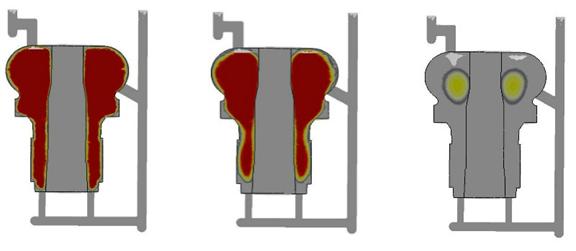
Рис. 3. Кристаллизация превентора из стали марки 30ХМЛ:
(а) относительная доля твердого вещества по окончании процесса заливки, (б) – через 27 мин после окончания заливки, (в) – через 95 мин. после окончания заливки (0 – жидкий металл, 1 – затвердевший металл)
Был выполнен анализ процесса для двух марок стали. В первом случае исследован процесс кристаллизации стали марки 42CrMoV, материал формы – специальная песчано-смоляная смесь alfaset. Начальные температурные поля заданы постоянными. Заливка проводилась 35 секунд. В ходе данного моделирования были получены картины затвердевания (рис. 2), позволяющие оценить время кристаллизации изделия.
Во втором случае исследован процесс кристаллизации стали марки 30ХМЛ, материал формы и параметры процесса аналогичны первому случаю. Также были получены картины доли затвердевшего металла (рис. 3).
Проведено сравнение картин пористости в готовом изделии, изготовленном в ходе натурного эксперимента, и результатов, полученных в ходе численного эксперимента (рис. 4). Сравнение показало, что существенных различий в картинах нет, результаты численного эксперимента удовлетворительно соответствуют натурным данным.

Рис. 4. Сравнение картин пористости
Заключение
Таким образом, на основе численного моделирования изучена эволюция температурных полей в процессе кристаллизации слитка при изготовлении литой заготовки превентора. Дан прогноз времени полной кристаллизации изделия, установлены места локализации возможных литьевых дефектов в виде пор. Картина распределения пористости подтверждена экспериментально на препарированном образце литой заготовки.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ (договор № 02.G25.31.0068 от 23.05.2013 г. в составе мероприятия по реализации постановления Правительства РФ № 218).
Рецензенты:
Столбов В.Ю., д.т.н., профессор кафедры математического моделирования систем и процессов Пермского национального исследовательского политехнического университета, г. Пермь.
Шардаков И.Н., д.ф-м.н., профессор, заведующий лабораторией Института механики сплошных сред Уральского отделения Академии наук, г. Пермь.



