При создании программного обеспечения систем автоматизированного управления энергетическими установками с электрическими машинами переменного тока, а также автоматизированных систем испытаний и диагностики машин переменного тока возникает необходимость в определении параметров синусоидальных сигналов, снимаемых с датчиков тока и напряжения в установившихся режимах, и точек огибающих этих сигналов в переходных режимах. К параметрам сигналов относятся: частота, начальная фаза, амплитудные и действующие значения напряжения и тока, а также угол сдвига фаз между напряжением и током. От точности определения этих параметров зависит точность определения других важных параметров электрических машин: коэффициента мощности, активной и реактивной мощности, потерь и КПД машины. От точности определения огибающих сигналов зависят показатели качества систем регулирования и управления и точность определения постоянных времени и других динамических параметров электрических машин.
Методология и результаты
В процессе автоматизированного съема информации проблема точного определения параметров токов и напряжений в установившихся режимах и их огибающих в переходных режимах осложняется появлением в измерительных каналах помех и шумов, искажающих регистрируемые значения. В связи с этим возникает необходимость использования при обработке на компьютере эффективных методов фильтрации.
Из рассмотренных эффективных методов фильтрации следует выделить метод, который основан на использовании быстрого преобразования Фурье входного сигнала, ограниченного с помощью окна Ханна. После разложения сигнала отыскивается гармоника с наибольшей амплитудой, для которой и определяются параметры сигнала [7]. Данный метод использован в виртуальном приборе «Extract Single Tone Information VI» из поставки программной среды разработки «LabVIEW» компании «National Instrument®» [5]. А для определения точек огибающих синусоидального сигнала в переходных режимах следует выделить метод, который основан на аппроксимации кубическим сплайном точек положительных и отрицательных вершин сигнала [4]. При реализации метода требуется использование виртуального прибора «Cubic Spline Fit» [8].
В настоящей работе для определения основных параметров и огибающих синусоидальных сигналов в установившихся и переходных режимах предлагается единый метод скользящей тригонометрической аппроксимации, который, как показали проведенные исследования, обладает лучшими фильтрующими свойствами, чем вышеуказанные.
Сигнал, снимаемый в установившемся режиме с датчика тока или напряжения электрической машины переменного тока, можно представить в виде:
y* = n(t) + A*sin(ω*t + ψ*), (1)
где n(t) – аддитивная случайная составляющая сигнала.
Аналитические преобразования на основе метода наименьших квадратов и разностных уравнений позволили получить следующие выражения:
– для вычисления угловой частоты
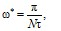 (2)
(2)
где τ – шаг квантования по времени,
N – число точек на половине периода;
– для вычисления амплитуды
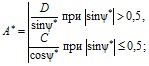 (3)
(3)
– для вычисления начальной фазы
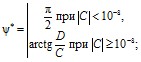 (4)
(4)
– для вычисления коэффициентов
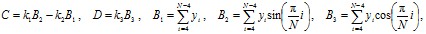
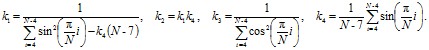
Гарантированную точность вычисления параметров сигнала обеспечивает следующий алгоритм:
- приближенное определение точек перехода через нуль синусоидального сигнала (напряжения и тока) на основе анализа точек, тяготеющих к около нулевой зоне;
- приближенное определение периода и угловой частоты на основе данных точек;
- расчет амплитудных значений синусоидального сигнала по приведенным выражениям;
- перевод синусоидального сигнала в относительные единицы;
- разбиение полученного сигнала на интервале 4 периодов на массивы длиной в 1/4 периода, симметричных относительно нуля;
- аппроксимация каждого из полученных массивов на участке от –π/6 ÷ π/6 уравнением регрессии первого порядка по методу наименьших квадратов и определение их коэффициентов;
- нахождение «истинных» нулей синусоидального сигнала на основе найденных коэффициентов уравнений;
- определение средних значений периода, начальной фазы и амплитуды на всем снятом процессе на основе «истинных» нулей;
- определение среднего значения угла сдвига фаз между напряжением и током на всем снятом процессе на основе «истинных» нулей.
Данный алгоритм был реализован в новом виртуальном приборе программной среды разработки «LabVIEW» [1, 3]. Сравнительный анализ результатов исследования показывает, что предложенный виртуальный прибор обеспечивает более точное определение параметров сигналов напряжения и тока чем стандартный лицензионный прибор «Extract Single Tone Information VI».
В частности, при уровне помех 20% от уровня полезного сигнала, среднеквадратичные отклонения погрешностей предложенного виртуального прибора и стандартного составляют при определении: частоты, соответственно, 0.25 % и 0,45 %; амплитуды – 2 % и 2,5 %; начальной фазы – 1 % и 2 %; угла сдвига фаз 0,5 % и 2,5 %.
В общем виде почти всякий переходный процесс рассматриваемых режимов работы машин переменного тока может быть представлен конечной суммой затухающих составляющих:
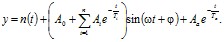 (5)
(5)
Исследования показали, что если наименьшая постоянная времени удовлетворяет условию Tmin ≥ π/2ω (что соблюдается в большинстве практических случаев), то переходный процесс на участках, прилегающих к экстремальным точкам (т. е. возле амплитудных значений), может быть с достаточной степенью точности аппроксимирован эквивалентной синусоидой, т. е. функцией вида
y* = A0* + A1* sin(ωt + ψ*) . (6)
Аналитические преобразования на основе метода наименьших квадратов и разностных уравнений позволили получить следующие выражения (мало отличающихся от предыдущих), по которым вычисляются параметры аппроксимирующей функции для каждого конкретного участка:
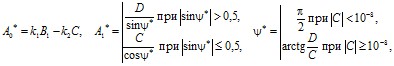
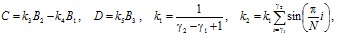
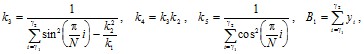
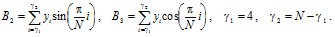
Координаты точек огибающей для рассматриваемого j-го участка процесса будут следующими:
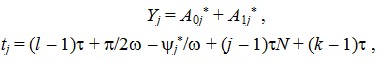 (7)
(7)
где l - номер начальной точки интервала обработки.
Установлено, что погрешность вычисления Yj , tj зависит от следующих факторов:
- от расположения экстремальной точки в пределах участка;
- от границ участка (оптимальные значения γ1 = π/6; γ2 = 5π/6 );
- от количества зарегистрированных значений на отрезке длиной в полпериода функции (для относительной погрешности квантования не более 1% N ≥ 25);
- от точности определения периода функции для рассматриваемого участка.
В случае искажения исходной информации влиянием помех и шумов, к данным факторам добавляется зависимость погрешности от закона распределения случайной составляющей n(t) (5).
Для получения гарантированной точности вычисления координат огибающих по всему переходному процессу разработан алгоритм скользящей аппроксимации с адаптацией ее параметров к конкретным свойствам обрабатываемого процесса (рис. 1).
В алгоритме можно выделить следующие основные операции:
- разделение процесса на зоны, в пределах каждой из которых период функции можно считать постоянным;
- центрирование, т. е. определение границ (γ1; γ2) областей, «тяготеющих» к экстремальным точкам;
- аппроксимация процесса в каждой области;
- уточнение среднего периода колебаний в пределах зоны;
- определение координат точек огибающих через параметры аппроксимирующей функции.
Операция центрирования заключается в смещении начала координат, за счет параметров сдвига k (7), таким образом, чтобы экстремальная точка (ордината огибающей) находилась, по возможности, в середине рассматриваемой области. Она осуществляется за счет итерационного процесса адаптации начальной фазы ψj* к срединному положению экстремума.
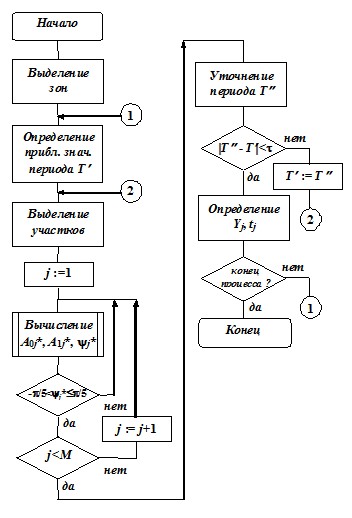
Рис. 1. Блок-схема алгоритма определения огибающих переходных процессов
Период колебаний в каждой области адаптируется к среднему периоду зоны.
Исследования показали, что алгоритм скользящей тригонометрической аппроксимации обеспечивает надежное определение точек огибающих переходных и квазиустановившихся процессов машин и аппаратов переменного тока. Он был реализован в новом виртуальном приборе комплекса программ для автоматизации испытаний синхронных турбомашин [2, 6].
Анализ результатов тестирования виртуального прибора на модельных процессах и на процессах, которые были зафиксированы при заводских стендовых испытаниях, показал: при числе точек на половине периода N = 25 и разрядности числа в 16 бит относительная погрешность предложенного метода при вычислении координат точек огибающих не превышает 1% ; при появлении случайной составляющей, доходящей до 30 % от уровня полезного сигнала, относительная погрешность не превышает 3 %. Такое значение погрешности обусловлено тем, что для выделения огибающих используются только участки кривой переходного процесса возле экстремальных точек.
Заключение
Для определения параметров синусоидальных сигналов, снимаемых с датчиков тока и напряжения машин переменного тока в установившихся режимах, и для определения точек огибающих этих сигналов в переходных режимах, предложен единый метод скользящей тригонометрической аппроксимации. Метод использован в алгоритмах новых виртуальных приборов программной среды разработки «LabVIEW». Как показали проведенные исследования, предлагаемые виртуальные приборы обеспечивают при появлении помех и шумов в измерительных каналах более точное определение основных параметров сигналов и их огибающих, чем лицензионные стандартные виртуальные приборы.
Рецензенты:
Казанцев В.П., д.т.н., доцент, профессор кафедры «Микропроцессорные средства автоматики», Пермский национальный исследовательский политехнический университет, г. Пермь;
Цаплин А.И., д.т.н., профессор, заведующий кафедрой «Общая физика» Пермского национального исследовательского политехнического университета, г. Пермь.



