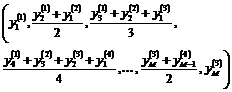Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

На современном оптовом рынке электрической мощности (ОРЭМ) электроэнергия покупается по регулируемым договорам длительностью один год, заключаемым, как правило, в начале года. В них фиксируются цены и объемы поставляемой электроэнергии. Эти цены регулируются администратором торговой системы (АТС). (Например, в 2007 г. данный вид закупок составлял 80−90% общего объема рынка ОРЭМ.) Начиная с 2008 г. объем данного вида закупок на рынке ОРЭМ последовательно уменьшался такими темпами, что 2012 г. должен был снизиться до нуля. Высвободившиеся объемы электроэнергии и мощности продаются на рынке на сутки вперед (РВС). Отмеченные обстоятельства являются экономическим стимулом более качественного планирования энергопотребления и энергопроизводства на сутки вперед, являющегося необходимым условием извлечения максимальной прибыли из краткосрочных договоров.

С математической точки зрения накопленная информация о динамике цен на ОРЭМ представляет собой некоторый временной ряд (ВР), и соответственно задача экономического прогнозирования цен на ОРЭМ сводится к задаче прогнозирования значений данного ВР. Однако обсуждаемые ВР оказываются трудно прогнозируемыми вследствие большого количества факторов, оказывающих на них влияние: объемов производства и потребления электроэнергии, графиков ремонтов генерирующего и сетевого оборудования, погодных условий, состава генерирующего оборудования, уровня водности, ценовых стратегий участников и т.п. (Например, совместная генерация тепловой и электрической энергии на ТЭЦ непрямую зависит от температуры окружающего воздуха [5], определяющей, в соответствии с нормативными требованиями, количество сжигаемого топлива и режимы работы турбин.)

Как следствие, точность результатов прогнозирования среднесуточных и часовых значений цен на рынке ОРЭМ, размещенных на сайте [6], оказывается относительно невысокой. Например, в 2010 г., как показывает анализ разности между спрогнозированными и фактическими значениями, 40% часовых прогнозов имели точность ниже 10%, 28% часовых прогнозов − 5−10%, 32% часовых прогнозов − выше 5%. Недостаточная точность прогнозирования обусловила использование с августа 2011 г. для прогнозирования рассматриваемого ВР еще одного метода (результаты, получаемые при его использовании на сайте [6] называются «Прогноз_К»), которые, однако, как и первый метод прогнозирования, на сайте не называются. При этом, как показывает анализ погрешностей прогнозирования, каких-либо улучшений качества прогнозирования не произошло.

Таким образом, задача повышения точности прогнозирования ВР, содержащего среднечасовые значения цен на ОЭРМ, остается актуальной.

В статье обсуждаются особенности нейросетевого прогнозирования изучаемого ВР с помощью ИНС [4]. (Примеры успешного использования ИНС для прогнозирования социально-экономических показателей в энергетической сфере можно найти в [1;2].)

Методика прогнозирования ВР на основе нейросетевых моделей

Методика прогнозирования ВР с помощью нейронных сетей реализуется следующей последовательностью действий [4].

1. Выбор вида нейронной сети, в том числе типа нейрона и вида функции активации.

2. Выбор количественных значений параметров: числа слоев сети, числа нейронов в слое, размера входного вектора значений, размера выходного вектора значений.

3. Обучение искусственной нейронной сети на известных множествах входных , ( – мерный вектор), векторов и соответствующих выходных векторов (мерный вектор).

4. Вычисление для каждого мерного входного вектора M прогнозируемых значений ВР.

Из общего описания методики нейросетевого прогнозирования ВР видно, что ее использование предполагает задание значений множества перечисленных выше параметров искусственной нейронной сети. При этом необходимо отметить, что универсальных рекомендаций по выбору данных параметров на сегодняшний день не существует, но можно предположить, что здесь целесообразно учитывать особенности прогнозируемого ВР.

Исследование частотно-временных характеристик ВР, содержащего часовые цены на ОРЭМ

Рассмотрим ВР, образованные индексами часовых цен на ОРЭМ по европейской ценовой зоне России в период с 1 марта 2009 г. по 25 марта 2011 г. по данным [6] (рис. 1). Количество членов временного ряда N = 18981.

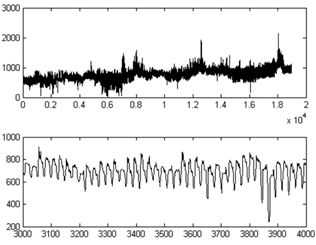
Рис. 1. Визуализация ВР, содержащего значения часовых цен на электроэнергию (руб./Мвт·час) в период с 1.03.2009 по 31.05.2011 г. от времени (начало отсчета − 0 час. 1 марта 2009 г., период дискретизации ВР − 1 час) (сверху − исходный ВР, снизу − фрагмент ВР).

Анализ зависимостей, представленных на рис. 1, позволяет предположить, что они представляют собой некоторую линейную комбинацию тренда , нескольких периодических составляющих 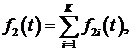а также случайных составляющих

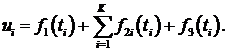(1)

Для подтверждения данного предположения на первом шаге была проверена гипотеза о возможности описания тренда линейной зависимостью. Для этого с помощью метода наименьших квадратов была найдена линейная аппроксимация рассматриваемого ФВР:

u(t)= 0,018074·t + 585,304209,

который далее был удален из ВР. ФВР, получившийся после удаления линейного тренда, и его гистограмма представлены на рис. 2.

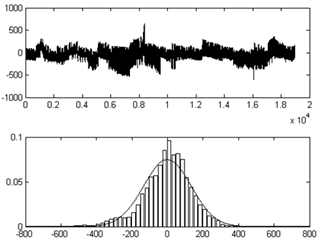
Рис. 2. Визуализация ФВР с исключенным линейным трендом (сверху − анализируемый ВР, снизу − гистограмма данного ВР).

Проверка распределения остатков по критериям Колмогорова-Смирнова (значение критерия 0.04905) и Лиллиеформа показала, что вероятность ошибки при отклонении гипотезы о согласии данного распределения нормальному распределению не превышает 0.01 (соответственно, критический уровень равен 0.05). Следовательно, распределение остатков ВР с удаленным линейным трендом оказывается отличным от нормального распределения. Данный результат, с нашей точки зрения, объясняется следующими причинами:

1) функция оказывается нелинейной;

2) в ФВР с удаленным линейным трендом присутствуют детерминированные периодические составляющие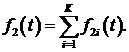

Для проверки предположения о наличии в рассматриваемом ВР детерминированных периодических составляющих было использовано оконное преобразование Фурье, предложенное Д. Габором [7]. (Напомним, что данное преобразование зависит от следующего набора параметров: размера скользящего окна W, величины перекрытия текущего и предыдущего окон W0, а также количества точек Nf, по которым вычисляются коэффициенты ряда Фурье.) Применение данного преобразования к ВР позволяет получить на последовательных временных интервалах набор спектров (следуя [3], «мгновенных» спектров). Для стационарного ВР форма данных спектров, как очевидно, будет одинаковой.

Для нестационарного временного ряда наличие набора мгновенных спектров позволяет вычислить средний спектр

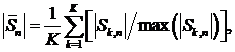
где n − номер спектральной гармоники, N− число спектральных гармоник, − число мгновенных спектров, и использовать в качестве количественно показателя «степени стационарности» ВР максимальное отклонение между средним и мгновенными спектрами:

На рис. 3 представлены усредненные мгновенные спектры ФВР для различных значений скользящего окна W (величина перекрытия соседних окон W0 = 0.8W, длина преобразования Фурье Nf = 4W). Здесь выбор размера окна выбирался кратным количеству отсчетов ВР, приходящихся на временной интервал длительностью 31 день.

Значения выбранного количественного показателя «степени нестационарности» ФВР представлены в табл. 1.

Из рис. 3 видно, что форма мгновенных спектров ФВР с удаленным линейным трендом при изменении в выбранном диапазоне размера окна оказывается подобной − основной вклад в энергию спектра вносят гармоники, частоты кратны 24/m час, m = 1,2,…. Увеличение размера окна W, с одной стороны, приводит к появлению дополнительных спектральных составляющих (в том числе, удается выделить составляющую с периодом, равным 1 неделе) и уменьшает, как видно из табл. 1, вариабельность мгновенных спектров, с другой.

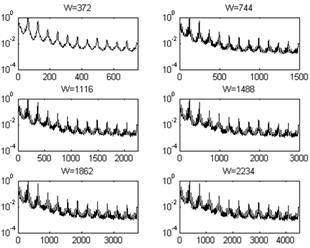
Рис. 3. Усредненные мгновенные спектры ФВР с удаленным линейным трендом (ось абсцисс − номер гармоники n, ось ординат −).

Таблица 1

К оценке устойчивости мгновенных спектров ФВР с удаленным линейным трендом

Таким образом, полученные результаты позволяют классифицировать ФВР на временных интервалах длительностью от полумесяца до трех месяцев как «квазистационарный» и использовать для его описания математическую модель (1). При этом для оценки параметров линейного тренда целесообразно использовать временные интервалы длительностью один год и более. Полученные оценки длительности интервалов «квазистационарности» анализируемого ВР были использованы при выборе размеров входного и выходного векторов.

Обоснование выбора параметров нейронной сети при прогнозировании ВР, содержащего среднечасовые цены на ОРЭМ

В данном исследовании в качестве элементарной единицы ИСН (нейрона) был выбран перцептрон [4]. Для выбора архитектуры ИНС была исследована зависимость точности прогнозирования исследуемого ВР от количества входных нейронов n_in, количества выходных нейронов n_out, количества нейронов на скрытом слое (слоях) n_hide. Персептроны обучались на основе алгоритма Левенберга-Марквардта, для обучения использовалось 3 пары обучающих выборок «вход»–«выход», взятых из известных значений ВР (рис. 4). Всего было рассмотрено 18 различных модификаций ИНС.

Для нейронной сети каждого вида выполнялось 100 статистических испытаний, в каждом из которых ИНС обучалась и далее использовалась для прогнозирования. Одна итерация включала в себя:

1. Создание и обучение нейронной сети: формирование входных и выходных обучающих выборок, создание ИНС, ее обучение на известных значениях ВР.
2. Прогнозирование – формирование нейронной сетью выходной выборки при подаче входного вектора, отличного от векторов, использованных при обучении.
3. Вычисление ошибок прогноза (абсолютных разностей между фактическими и спрогнозированными значениями) в каждой конкретной точке, средней ошибки для всего прогнозируемого участка.

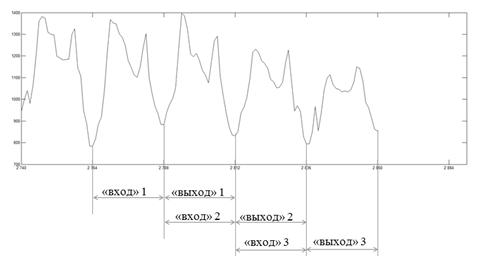
Рис. 4. Обучающие выборки.

Средние ошибки прогнозирования для каждого изученного типа ИНС представлены в табл. 2.

Таблица2

Средние ошибки прогнозирования различных ИНС

Из табл. 2 видно, что средняя ошибка прогнозирования оказывается наименьшей, когда количество выходных нейронов (число прогнозируемых точек) оказывается равным одному периоду недельной составляющей изучаемого ВР (168 точек). При этом наименьшая ошибка прогноза оказывается при использовании ИСН№16 (табл. 1).

Анализ результатов прогнозирования ВР, содержащего среднечасовые цены на ОРЭМ

Представляет интерес сравнить результаты прогнозирования ИНС, параметры которой выбраны в соответствии с приведенными выше рекомендациями, с аналогичными результатами, приведенными на сайте [6].

Здесь прогнозирование с помощью ИНС №16 выполнялось 2 способами.

1. Последовательные прогнозы: новая ИНС обучалась и прогнозировала данные, «сдвинутые» на неделю относительно предыдущей ИНС (рис. 5).

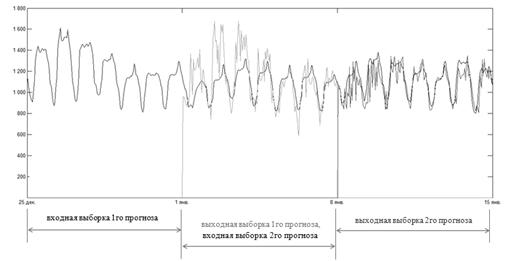
Рис. 5. Иллюстрация вычисления последовательных прогнозов.

2. Накапливаемые прогнозы (формулы для вычисления прогнозируемых значений, получаемые на первых трех шагах прогнозирования, представлены в табл. 3).

Таблица 3

Формулы для вычисления прогнозируемых значений, получаемые на первых четырех шагах накапливаемого прогноза

Рассмотрим результаты анализа погрешности прогноза, выполненного на отрезке ВР в период с 01.01.2014 по 20.04.2014 (табл. 4).

Таблица 4

Результаты анализа точности прогнозирования

Из табл. 4 видно, что наиболее точными оказываются результаты прогнозирования при использовании накапливаемого прогнозирования методом ИНС, так как у 63% спрогнозированных значений ВР погрешность прогнозирования не превосходила 5%, и только у 8% спрогнозированных значений ВР погрешность прогнозирования превосходила 10%.

Более высокая точность прогнозирования методом накапливаемого прогнозирования в сравнении с последовательным прогнозом объясняется тем, что обучающая выборка, а также вектор входных значений имеют случайную составляющую, которая с неизбежностью будет присутствовать и в прогнозируемых значениях. В этих условиях использование процедуры усреднения по нескольким прогнозам позволяет уменьшить вклад случайной составляющей и, соответственно, обеспечить более высокую точность прогнозирования.

Заключение

Результаты исследования нейросетевого прогнозирования ВР, содержащего значения часовых цен на ОРЭМ, позволяют сделать следующие выводы.

1. При использовании нейросетевых моделей для прогнозирования ВР архитектуру и параметры ИНС следует выбирать с учетов частотно-временных характеристик изучаемых ВР.
2. Наибольшую точность нейросетевого прогноза ВР, представляющего собой линейную комбинацию тренда и гармонических составляющих,обеспечивает архитектура многослойного персептрона, в которой количество входных и выходных нейронов равно периоду основной гармоники прогнозируемого ВР.
3. ИНС обеспечивают более высокую точность прогнозирования в сравнении с методами прогнозирования, используемыми на сайте [2].

Работа выполнена в рамках договора № 02.G25.31.0055 (проект 2012-218-03-167) при финансовой поддержке работ Министерством образования и науки Российской Федерации.

Рецензенты:

Доросинский Л.Г., д.т.н., профессор, заведующий кафедрой теоретических основ радиотехники Уральского федерального университета им. первого Президента России Б.Н. Ельцина, г. Екатеринбург.

Суханов В.И., д.т.н., доцент, заведующий кафедрой микропроцессорной техники Федерального автономного государственного образовательного учреждения высшего профессионального образования «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург.