Современная система школьного математического образования постоянно изменяется как в содержании, так и в формах и в методах преподавания. В основу нового федерального государственного образовательного стандарта среднего (полного) общего образования положен системно-деятельностный подход, который обеспечивает формирование готовности к саморазвитию и непрерывному образованию; проектирование и конструирование развивающей образовательной среды для обучающихся; активную учебно-познавательную деятельность обучающихся; построение образовательного процесса с учётом индивидуальных возрастных, психологических и физиологических особенностей обучающихся [1,7,8].В связи с этим актуальной является проблема разработки таких средств обучения и методик их использования, которые, во-первых, способствовали бы формированию и развитию познавательной активности и самостоятельности школьников, во-вторых, позволяли бы учитывать индивидуальные особенности обучаемых в процессе изучения математики.
В настоящее время в теории и методике преподавания математики накоплен богатый опыт организации конструктивной, созидательной деятельности учащихся. Вместе с тем, в школьной практике, к сожалению, до сих пор нередко ученик находится в положении объекта передаваемой ему извне информации [2,5]. Изучение нового материала зачастую ограничивается объяснением этого материала учителем с последующим заучиванием детьми правил, теорем, определений понятий. Результатом такого подхода является формализм в знаниях учащихся, недостаток или отсутствие исследовательских умений, низкий уровень творческого мышления.
С целью устранения этой проблемы многие творчески работающие учителя используют в ходе изучения нового материала эвристический метод обучения. Посредством постановки ряда последовательных вопросов и заданий, они вовлекают школьников в процесс «открытия» различных математических фактов, что, безусловно, способствует активизации познавательной мыслительной деятельности обучаемых [3]. В то же время эвристическая беседа подразумевает использование фронтальной формы организации учебной работы, при которой учитель объективно не в состоянии обеспечить одинаковую активность всех учеников класса, проследить за ходом мысли каждого отдельного ученика.
Эффективной формой обучения, позволяющей организовать эвристическую деятельность учащихся в процессе изучения нового материала и при этом избежать указанного недостатка, является, на наш взгляд, дифференцированная самостоятельная работа[6]. Во-первых, такая работа способствует активизации познавательной деятельности каждого учащегося, так как она носит индивидуальный характер и ни один ученик не сможет воспользоваться результатами и выводами своих товарищей [4]. Во-вторых, варьирование числа заданий и использование различных форм их предъявления для разных типологических групп школьников позволяют учитывать индивидуальные особенности обучаемых в процессе организации самостоятельной работы. И, наконец, в-третьих, учитель получает возможность следить за ходом усвоения новой информации каждым учащимся и оказывать необходимую помощь в случае возникновения тех или иных затруднений в выполнении заданий самостоятельной работы.
Проиллюстрируем сказанное на примере дифференцированной самостоятельной работы, которая может быть организована при изучении темы «Свойства логарифмов».
ВАРИАНТ 1.
Задание 1. Вычислите:
Сравните результаты, полученные в левом и правом столбце. Какую закономерность вы обнаружили?
Сформулируйте гипотезу:
, где 
Проверьте ее справедливость при 
.
Задание 2. По основному логарифмическому тождеству 
,
. Найдите произведение левых и правых частей этих равенств.
Указание. Используйте свойство степени 
Запишите полученные результаты:
Левая часть: 
, правая часть: . Какое равенство у вас получилось?
Заполните пропуски: 
а 
= b · 
.
Подумайте, как из равенства получить равенство 
.
Указание. Воспользуйтесь определением логарифма.
Итак, вы доказали первое свойство логарифмов:
|
|
, где 
.
Приведите свой пример, иллюстрирующий это свойство:
, 
, 
. Тогда 
+ 
= 
.
Задание 3. Вычислите:
Сравните результаты, полученные в левом и правом столбце. Сформулируйте второе свойство логарифмов:
, где
Проверьте его справедливость при 
.
Задание 4. Заполните пропуски в доказательстве второго свойства логарифмов.
По основному логарифмическому тождеству ___,___. Найдем частное____. В результате получим равенство____. Тогда по определению логарифма получим ________.
Итак, вы доказали второе свойство логарифмов:
|
|
, где 
.
Проверьте его справедливость при .
Приведите свой пример, иллюстрирующий это свойство:
, , . Тогда - = .
Задание 5. Вычислите:
Какое предположение можно сделать? Сформулируйте третье свойство логарифмов:
= 
, где 
,
, 
, 
.
Проверьте его справедливость при 
.
Задание 6. По основному логарифмическому тождеству 
. Возведите левую и правую части этого равенства в степень с показателем р:
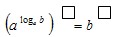или по свойству степени 
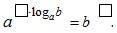. Тогда по определению логарифма получится 
.
Итак, вы доказали третье свойство логарифмов:
|
|
, где 
.
Приведите свой пример, иллюстрирующий это свойство.
ВАРИАНТ 2.
Задание 1. Вычислите:
Сравните результаты, полученные в левом и правом столбце. Какую закономерность вы обнаружили? Сформулируйте гипотезу:
,
, где , , .
Проверьте ее справедливость при 
.
Задание 2. Докажите полученные свойства логарифмов.
Указание. По основному логарифмическому тождеству , 
. Для доказательства первого свойства нужно найти произведение этих равенств, для доказательства второго свойства, соответственно, их__________.
Какие равенства у вас получились? Заполните пропуски:
а 
= b · 
, 
= 
/ 
.
Подумайте, как из равенств 
и 
получить равенства 
и 
.
Указание. Воспользуйтесь определением логарифма.
Итак, вы доказали первое и второе свойства логарифмов:
|
где |
, 
,
.
Приведите свои примеры, иллюстрирующие эти свойства:
, , . Тогда ? + ? = ?
. 
, , . Тогда ? - ? = ? .
Задание 3. Вычислите:
Какое предположение можно сделать? Сформулируйте третье свойство логарифмов:
?= , где , , .
Проверьте его справедливость при 
.
Задание 4. Докажите третье свойство логарифмов.
Указание. По основному логарифмическому тождеству . Возведите левую и правую части этого равенства в степень с показателем р и воспользуйтесь определением логарифма.
Итак, вы доказали третье свойство логарифмов:
|
|
, где Приведите свой пример, иллюстрирующий это свойство.
ВАРИАНТ 3.
Задание 1. Вычислите:
Сравните результаты, полученные в левом и правом столбце. Какую закономерность вы обнаружили? Сформулируйте гипотезу:
, 
,
? = 
, где , , , 
р 
.
Задание 2. Докажите полученные свойства логарифмов.
Указание. Воспользуйтесь основным логарифмическим тождеством, свойствами степени и определением логарифма.
Проверьте правильность выполненных доказательств свойств логарифмов по учебнику.
Организуя самостоятельную эвристическую деятельность учащихся на этапе непосредственного получения информации, необходимо учитывать в первую очередь такие качества мышления обучаемых, как способность к восприятию информации, ее осмыслению и запоминанию, уровень сформированности общеучебных умений, таких как умение наблюдать, сравнивать, анализировать и т.п. Поэтому в качестве основного параметра, определяющего дифференциацию самостоятельных работ на данном этапе, целесообразно выбрать уровень эвристичности познавательной деятельности. В зависимости от этого уровня меняется характер познавательной деятельности школьников, который должен быть отражен в том или ином варианте самостоятельной работы.
В случае, когда уровень эвристичности познавательной деятельности достаточно низок, учащимся может быть предложен первый вариант самостоятельной работы. В процессе его выполнения ученики получают новую информацию преимущественно в готовом виде. Познавательная деятельность обучаемых при выполнении таких заданий осуществляется главным образом на репродуктивном уровне. Второй вариант самостоятельной работы, соответствующий среднему уровню эвристичности познавательной деятельности, предполагает расширение доли поисковой деятельности ученика при получении новой информации. Наконец, третий вариант самостоятельной работы, соответствующий высокому уровню эвристичности познавательной деятельности, предполагает получение новой информации преимущественно в процессе поиска.
Ценность дифференцированных самостоятельных работ, содержащих задания эвристического характера, заключается в том, что познание математических фактов или закономерностей сопровождается высокой умственной активностью детей, напряжением интеллектуальных сил. А это стимулирует учебную деятельность, способствует более глубокому проникновению в сущность изучаемых закономерностей, более прочному запоминанию учебного материала.
Рецензенты:
Фролов И.В., д.п.н., профессор, заведующий кафедрой физики, теории и методики обучения физике Арзамасского филиала «Нижегородский государственный университет им. Н.И. Лобачевского», г. Арзамас;
Санина Е.И., д.п.н., профессор кафедры общих математических и естественнонаучных дисциплин ГБОУ ВПО МО «Академия социального управления», г. Москва.