В конце 60-х годов прошлого века венгерский биолог и ботаник Аристид Линденмайер (1925-1989) предложил описывать процессы биологического роста и размножения посредством L-систем - набора простых итерационных правил, преобразующих знаки некоторого алфавита. В 50-х годах прошлого века Ноам Хомский предложил схожую алгоритмическую модель, применимую для анализа и построения грамматик языка.
В данной работе обсуждаются возможности использования подхода и модели Линденмайера для моделирования роста территориальных кластеров и анализа кластерной политики региона.
Рассмотрим множество G-факторов регионального развития, влияющих на кластерную политику, в виде:
G = {X, r, ω, P}, (1)
где:
X – множество из k переменных, описывающих состояние кластеров региона в разные моменты времени n;
r – множество констант, влияющих на рост X (например, константы – катализаторы и константы – ограничители роста),
ω – множество, описывающее начальное состояние региона в виде набора некоторых переменных и констант: , , ,
P – множество правил преобразования переменных на шаге преобразования от к , к , …, от к .
Рассмотрим и формализуем простейшую модель модель спин-офф проектов териториального кластера по модели Линденмайера.
Пусть за единицу времени (итерацию) «новая» компания А превращается в «старую» компанию В, а «старая» компания В формирует спин-офф – новую компанию А и остается в состоянии «старой» компании. Пусть в начальных условиях у нас есть «новая» компания.
С точки зрения L-систем эту задачу можно описать следующим образом:
Х (переменные): A, B
r (константы): нет.
ω (начальное состояние): A
P (правило): (A → B), (B → AB)
Пусть n – номер итерации или «поколения компаний» кластера. Запишем в скобках количество «новых» и «старых» компаний А и В:
Тогда:
n = 0: A (1),
n = 1: B (1),
n = 2: AB (2),
n = 3: BAB (3),
n = 4: ABBAB (5),
n = 5: BABABBAB (8),
n = 6: ABBABBABABBAB (13),
n = 7: BABABBABABBABBABABBAB (21).
В этой последовательности – начиная со второй единицы, следующее число получается сложением двух предыдущих, а количество компаний описывается последовательностью Фибоначчи:
1 1 2 3 5 8 13 21 34 55 89 ...
При этом график зависимости числа участников кластера от числа итераций будет устремляться к бесконечности по степенному закону (рис. 1).
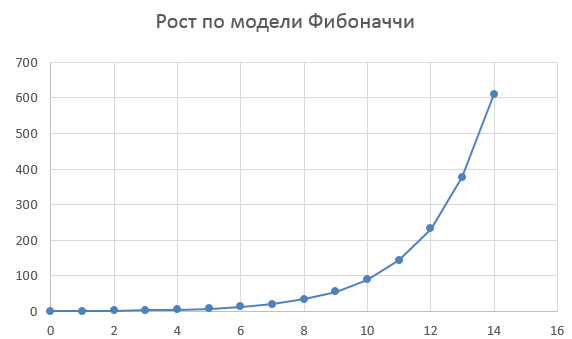
Рис. 1. График зависимости числа участников кластера от числа итераций.
Если мы рассмотрим предел деления двух соседних членов последовательности Фибоначчи
![]() ,
,
то обнаружим, что эта величина стремится к постоянному соотношению:
![]()
Это иррациональное число φ – так называемое золотое сечение. Золотое сечение находят в пропорциях человека, растений и животных. Его используют в биржевой торговле - техническом анализе рынков (так называемые волны Элиота). Это число часто встречается во множествах Жюлиа и Мандельброта – объектах фрактальной геометрии.
Фрактальные множества Бенуа Мандельброта могут быть интерпретированы как L-системы – результаты бесконечных итерационных преобразований.
В качестве примера рассмотрим построение с помощью L-системы знаменитого фрактала – канторовой пыли.
Это фрактальное множество было исследовано знаменитым математиком Георгом Кантором (1845-1918). В 1883 году Кантор публикует свою работу «Über unendliche, lineare Punktmannigfaltigkeiten», в котором демонстрирует пример построения «монстра» – множества точек, называемого сейчас множеством Кантора. Кантор последовательно отбрасывал из отрезка единичной длины сначала среднюю часть, а потом средние части всех оставшихся фрагментов. Проделав эту процедуру бесконечное число раз, великий логик рассмотрел свойства получившегося множества точек – так называемой канторовой пыли. Кантор показал парадоксальность этого «монстра». Мощность получившегося множества точек оказалась равной мощности множества точек на отрезке (рис. 2).

Рис. 2. Множество Кантора.
Запись построения канторовой пыли на языке L-систем:
Х (переменные): A, B
r (константы): нет.
ω (начальное состояние): A
P (правило): (A → ABA), (B → BBB).
Пусть А означает команду «рисовать отрезок», В – «продвинуться на отрезок без рисования».
Тогда:
n = 0: A,
n = 1: АВА,
n = 2: АВАВВВАВА,
n = 3: АВАВВВАВАВВВВВВВВВАВАВВВАВА.
Данный математический алгоритм может иметь экономический смысл при описании процессов формирования новых компаний кластера в зависимости от начального распределения компаний кластера и правил кластеризации – локализации новых компаний в окрестностях старых компаний. Кластерная политика формализуется через выявление правил кластеризации, а также констант - катализаторов и ограничителей роста.
Рассматриваемые нами примеры демонстрировали ничем не ограниченный рост участников кластера. Однако в экономической реальности это не так – рост компаний ограничивается объемами рынка, демографическими и институциональными особенностями.
Для моделирования ограничений роста рассмотрим Хn - количественный показатель роста и развития территориального кластера (например - объем продаж, число организаций-участников, количество связей (контрактов) между участниками, количество рабочих мест, количество занятых на предприятиях кластера), отражающий его эволюционную динамику в момент времени n.
Рассмотрим R – коэффициент роста кластера за единицу времени:
R = (Xn+1 - Хn ) / Хn .
Допустим, что товары и услуги кластера пользуются устойчивым неограниченным спросом на рынке и у кластера нет каких-либо ограничений в росте и развитии. В этом случае коэффициент R постоянен и равен s. Это означает, что за единицу времени показатель роста кластера увеличивается одинаково. Закон роста кластера выглядит следующим образом:
Xn+1 = (1+s) Хn .
Подставляя последовательно в это уравнение начальные условия, получим рост кластера по экспоненциальному закону:
Xn = (1+s)n Х0.
Пусть у роста кластера есть ограничение N (например, максимальный объем рыночного спроса на товары и услуги кластера, объем трудовых ресурсов, ограничение по энергетическим мощностями или инфраструктуре, ограничение на объем заказов от якорного предприятия кластера и пр.) выраженное в тех же количественных показателях, что и X.
Предположим, что в этом случае скорость роста кластера R должна зависеть от N. Установим, что кластер может расти по экспоненте только в том случае, если Xn намного меньше N – если показатель роста далек от насыщения N.
Как только Xn становится по порядку величины схожим с N или приближается к N, скорость роста кластера резко уменьшается, а динамику кластера начинает определять близость Х к N.
C учетом этих представлений запишем R следующим образом:
R = r (N - Хn ),
где r – константа, которую мы будем называть константой роста.
Итак, когда Xn у нас намного меньше N, то R будет являтьcя почти что константой (вкладом Xn в R можно пренебречь), и мы будем наблюдать рост кластера по экспоненте.
При приближении параметров кластера к насыщению – значению N, рост кластера будет уменьшаться – значение R будет падать.
Приравняем новое установление R к его начальному определению. Мы получим:
R = r (N - Хn )= (Xn+1 - Хn ) / Хn
или:
Xn+1 = r (N - Хn ) Хn + Хn .
Примем N=1 (100%) и преобразуем это уравнение к виду:
Xn+1 = (1+ r) Хn - r Хn2 .
Это хорошо известное в теории хаоса и теории фракталов логистическое уравнение Ферхюльста. Для нас важно то, это уравнение является частным случаем (1) и логистическое уравнение Ферхюльста является L-системой:
Х (переменные): Х
r (константы): r, N
ω (начальное состояние): Х0
P (правило): Xn+1 = (1+ r) Хn - r Хn2
В качестве примера представим график зависимости Хn от n при Xn+1 =0,05 и r=2 (рис. 3).
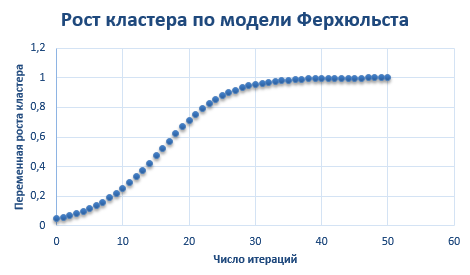
Рис. 3. График по модели Ферхюльста.
Феноменологически этот график демонстрирует различные этапы эволюции системы: рождение (в нашем случае - итерации от 0 до 10), развитие (от 10 до 20) и стабилизация на этапе насыщения (выше 20).
Есть очевидное и неслучайное внешнее подобие между данными, демонстрируемыми логистическими моделями, и эмпирическими данными динамики развития технологий и территориальных кластеров, которая фиксируется так называемыми S-образными кривыми инфраструктурного роста.
Анализ S-образных кривых позволяет определить этапы эволюции кластеров и технологических укладов, определить точки фазового перехода – смены режимов их функционирования (рис. 4).
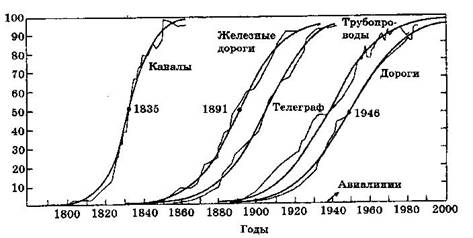
Рис. 4. S-образные кривые роста инфраструктуры США [6].
Можно предположить, что в экономике динамика кластеров и сумма технологий взаимозависимы, так как различные технологические уклады и кластеры являются друг для друга внешней средой. То, что для одних технологий и для одних кластеров является развитием, для других является деградацией и кризисом. Например, развитие железных дорог вызвало кризис в коннозаводческом бизнесе и деградацию регионов, на нем специализирующихся.
C точки зрения управления, описанные выше этапы эволюции можно интерпретировать как изменение режимов - смену вида управленческих обратных связей. На этапах рождения и функционирования доминируют отрицательные обратные связи, стабилизирующие систему и стремящиеся привести ее в равновесие. На этапах развития и деградации доминируют положительные обратные связи и система выходит из равновесного состояния, развиваясь к новым состояниям либо разрушаясь. Смена режима – это изменение типа обратной связи от внешней среды к системе. Анализируя динамику системы, можно достаточно рано выявить потерю устойчивости и выход на новый режим.
В качестве примера определим режимы развития инфраструктуры телеграфа в США. Для этого проведем касательную, как показано на рис. 5, и образуем треугольник АВС.
Этап развития АС определяется по пересечению касательной с «полом» и «потолком» - предыдущим и последующим стабильными уровнями функционирования системы.
Анализируя этот треугольник, можно установить, что режим развития системы телеграфа в США, выраженный в экспоненциальном росте инфраструктуры, продолжался с начала 80-х годов XIX века до начала 30-х годов ХХ века.
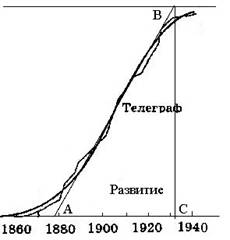
Рис. 5. Графическое определение периода развития телеграфа в США как расстояния между точками А и С.
Точки А и С – это точки фазового перехода системы развития телеграфа, после прохождения которых динамика системы поменялась.
До момента А и после момента С в системе господствуют отрицательные – стабилизирующие обратные связи. До точки А и после точки С система устойчива – социальные институты «надзирают» за ней и не дают развиваться.
На этапе рождения (до 80-х годов XIX века) телеграфу надо было преодолеть их сопротивление, вывести систему из равновесия. В 40-е годы ХХ века система насытилась и стала демонстрировать равновесное состояние.
Однако в какой-то момент инновация начинает уходить из под влияния стабилизирующих связей и надзорных механизмов.
Это уравнение хорошо моделирует «петлеобразную» структуру развития: «причиной» развития телеграфа после момента A становится развитие телеграфа – система выходит на лавинообразный этап самоорганизации.
Подобие между S-образными кривыми (репрезентирующими динамику инноваций и эволюционного цикла территориальных кластеров) и графиками логистических уравнений позволяет говорить о возможностях использования логистических уравнений и модели Линденмайера (L-систем) для моделирования и анализа кластерной политики региона.
Исходя из этого описания предлагается следующая последовательность концептуального моделирования и анализа кластерной политики региона.
-
Интерпретация множества переменных – количественных показателей, меняющихся в зависимости от роста и развития кластеров региона.
-
Интерпретация и описание констант роста и констант – ограничителей роста кластеров.
-
Описание множества начальных состояний ω в виде распределений переменных и значения констант.
-
Содержательная интерпретация механизмов преобразования переменных – параметров развития кластеров.
С точки зрения теории самоорганизации критичным является описание так называемых параметров порядка – набора констант и переменных, катализирующих и ингибирующих рост кластера. При этом перестройка структуры кластера связана со сменой параметров порядка.
Рецензенты:
Серегин С.Н., д.э.н., профессор, МГУТУ им. К.Г. Разумовского, г. Москва.
Смирнов В.Г., д.э.н., профессор, МГУТУ им. К.Г. Разумовского, г. Москва.



