Для изделий из магнитомягкого материала (МММ)основная кривая намагничивания (ОКН) является одной из важнейших характеристик. Методика выполнения измерений при определении ОКН изделия из МММ предусматривает два основных этапа [4].
На первом этапе перед измерением ОКН необходимо выполнить размагничивание образца посредством перемагничивания его в знакопеременном поле, с амплитудой равномерно убывающей от максимального до минимального значения (рис.1). Время размагничивания должно составлять не менее 40 с.
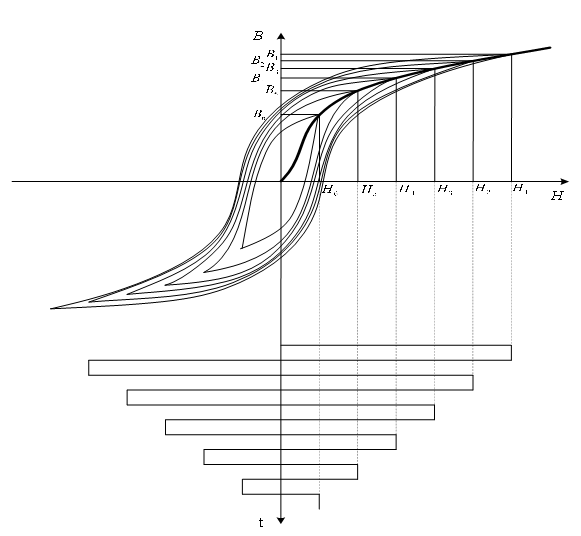
Рис. 1. Программа размагничивания
На втором этапе определение координат точек ОКН изделия из МММ начинают с наименьшего требуемого значения напряженности поля, постепенно переходя к большим значениям, при этом не допускается возврат от больших значений к меньшим [3].
Если в ходе первого этапа измерять амплитуду импульсов размагничивающего поля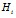
и приращения индукции
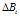, то можно проанализировав эти данные, определить минимальное число точек ОКН в которых требуется выполнить измерение для линейной аппроксимации ее с требуемой точностью.
Для этого был разработан алгоритм [5], позволяющий решить эту задачу. Работа алгоритма базируется на методе определения погрешности [1].
В основе алгоритма лежит анализ модуля второй производной изменения магнитной индукции B по напряженности H. Построив график зависимости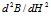 
от Н, вычисляем значение общей площади Sобщ. по формуле
.
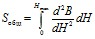Задавшись количеством точек n, определяем значение площади Sизм., соответствующей одной измеряемой точке на ОКН
.
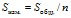Для нахождения координат точек, подлежащих измерению, воспользуемся формулой вычисления площади методом трапеции и уравнением прямой и составим систему уравнений:
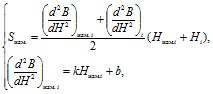(1)
где,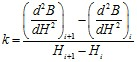 
, 
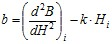– коэффициенты, 
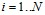, N – количество точек полученных в процесс проведения размагничивания.
Решая систему уравнений (1), получим:
.
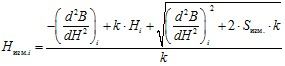После определения первой и второй производных (рис. 2), и применения выше описанного алгоритма получили результаты, представленные на рис. 3.
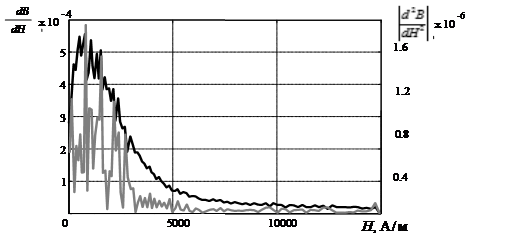
Рис. 2. Первая и вторая производные по Н
Рис.3.Результат применения алгоритма при n=10
Видно, что алгоритм работает некорректно. Данная «некорректность» вызвана сильным зашумлением результатов измерений ОКН.
Для исправления положения произведем фильтрацию. На рис. 4 представлены функции первой и второй производных измеренной ОКН после проведения фильтрации.
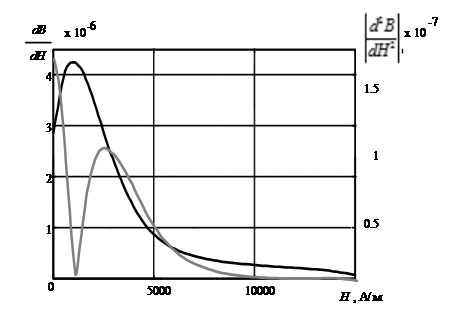
Рис. 4. Производные после фильтрации
На рис. 5 результаты, полученные после использования фильтрованных функций первой и второй производных в адаптивном алгоритме.
Рис. 5. Результат работы алгоритма при n=10
Из рисунка 5 видно, что алгоритм работает корректно, выделяя линейные и нелинейные участки ОКН и строя программу измерения таким образом, что на нелинейных участках проводиться максимальное количество измерений.
Таким образом, предложенный алгоритм оптимизирует количество измеряемых точек ОКН, увеличивая производительность операций контроля при погрешности измерения, не превышающей значения регламентируемого в [2].
Статья подготовлена с использованием оборудования ЦКП "Диагностика и энергоэффективное электрооборудование" ЮРГПУ(НПИ).
Рецензенты:
Нагай В.И., д.т.н., профессор кафедры «Электрические станции и электроэнергетические системы», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова, г. Новочеркасск.
Горбатенко Н.И., д.т.н., профессор кафедры «Информационные и измерительные системы и технологии», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова, г. Новочеркасск.