Проектные характеристики транспортной системы (ТС) региона ориентируются на обеспечение базовых плановых параметров ее функционирования. В процессе реальной эксплуатации каждый из структурных элементов ТС подвергается воздействию случайных (негативных) факторов, которые приводят к изменению (усложнению) условий функционирования. Случайный характер проявления негативных факторов приводит к необходимости проведения вероятностного анализа уровня надежности функционирования ТС.
Общая характеристика транспортной системы
Транспорт представляет собой одну из отраслей экономики. Структура транспортной системы для перемещения грузов и пассажиров представляется в виде подсистем транспорта общего и специального назначения (рис.1, [2]).
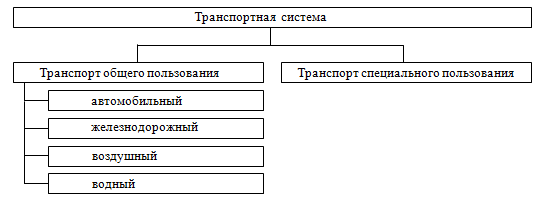
Рис.1. Структурная схема транспортной системы
Транспортная система для перемещения грузов и пассажиров представляет собой совокупность структурных элементов, которые находятся друг с другом в сложном взаимодействии и образуют определенную целостность.
ТС обладает следующими особенностями, присущими сложной технической системе:
- большое количество взаимодействующих элементов различного назначения, имеющих строго ориентированную структуру;
- подчиненность всех элементов и образуемых ими локальных подсистем одной целевой функции;
- наличие защитных элементов и систем, обеспечивающих защиту от сбойных ситуаций или устраняющих последствия отказов;
- возможность воздействия случайных факторов, приводящих к отказу элементов.
Для исследования сложных комплексных структурных образований используются понятие системы, совокупности функциональных подсистем, а также методы системного анализа [1].
Факторы, определяющие уровень надежности функционирования ТС называются системными, они имеют техническую или человеческую природу[1,5]. Технические факторы в свою очередь имеют моральную, этическую и социальную стороны. К внесистемным факторам относятся негативные факторы окружающей среды, не зависящие от внутренних свойств ТС.
Вероятностная модель транспортной системы
Проектные решения, принятые для обеспечения функционирования ТС региона являются обоснованием для функционирования системы в ожидаемых условиях.
Вероятностная модель, предназначенная для характеристики функционирования ТС региона, ориентирована на реализацию возможности учета случайных факторов, связанных с конкретными структурными особенностями и функционированием системы.
Вероятностная модель обеспечивает возможность проведения системного анализа располагаемой (проектируемой) пропускной способности ТС. С помощью модели возможно выявлять потенциальные источники негативных факторов, произвести оценку надежности функционирования и взаимодействия элементов ТС при возникновении особых ситуаций, определить количественное значение вероятности снижения пропускной способности ТС при воздействии негативных факторов.
Предположение о вероятности возникновения особой ситуации в ТС является рабочей оценкой возможного проявления закона случайных событий.
Исходные события модели
Область множества причин проявления факторов снижения надежности функционирования ТС включает следующие группы:
- отказы транспортной техники и вспомогательных машин и механизмов;
- ошибки персонала, занятого обеспечением транспортных процессов;
- неблагоприятные факторы окружающей среды.
Влияние каждой из этих групп на функционирование ТС оценивается частными аналитическими критериями, которые определяются при допущении независимости событий.
Для оценки интенсивности исходных событий (негативных факторов) используются: статистические критерии, экспертные оценки или директивные указания.
Статистические показатели интенсивности исходных событий – это единственно объективные характеристики и делятся на абсолютные и относительные показатели.
Вероятностную модель функционирования ТС можно рассматривать, как случайную непрерывную функцию или случайный процесс.
Модель марковского случайного процесса
Основной характеристикой процесса являются многомерные распределения вероятностей для фиксированных моментов времени.
Частный случайный процесс называется марковским, если вероятность каждого состояния системы в будущем зависит исключительно от состояния системы в настоящий момент и не зависит от того, каким образом система пришла в это состояние[2].
Марковский процесс - это процесс без последствия. Распределение вероятностей состояний системы для некоторого момента времени 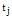 может быть выражено через распределение в предшествующий момент времени
может быть выражено через распределение в предшествующий момент времени 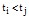 независимо от предшествующей истории процесса.
независимо от предшествующей истории процесса.
Для практических исследований предлагается марковский процесс с дискретным числом состояний системы и непрерывным временем, в котором имеется конечное число дискретных состояний некоторой системы u: 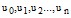 и указаны возможные пути перехода между состояниями.
и указаны возможные пути перехода между состояниями.
Если в некоторый момент времени система находилась в состоянии 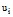 , то, независимо от своего поведения до этого момента
, то, независимо от своего поведения до этого момента 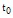 , она через время t с вероятностью
, она через время t с вероятностью 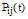 переходит в состояние
переходит в состояние 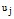 .Вероятности типа
.Вероятности типа 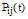 называются переходными вероятностями этого процесса. Если обозначить через
называются переходными вероятностями этого процесса. Если обозначить через 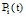 вероятность того, что в момент времени t система u будет находиться в состоянии
вероятность того, что в момент времени t система u будет находиться в состоянии 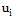 , то для любого момента времени сумма вероятностей состояний равна единице [4]:
, то для любого момента времени сумма вероятностей состояний равна единице [4]:
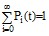 . (1)
. (1)
Решение задачи состоит в определении для любого 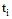 вероятности состояний
вероятности состояний 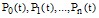 , соответствующих принятым дискретным состояниям системы
, соответствующих принятым дискретным состояниям системы 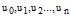 .
.
Возможность перехода между состояниями системы 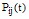 определяют количественные значения интенсивности вероятностей перехода между состояниями системы [3]:
определяют количественные значения интенсивности вероятностей перехода между состояниями системы [3]:
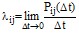 . (2)
. (2)
При малом значении 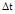 переходная вероятность
переходная вероятность 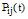 составляет:
составляет:
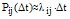 ; (3)
; (3)
Граф состояний модели
Для анализа функционирования ТС разработана математическая модель, которая описывает протекание марковского процесса с дискретным числом возможных состояний в виде вершин графа состояний и переходов состояний (рис. 2).
Граф состояний характеризует физическую систему (ТС), в которой протекает случайный процесс в течение времени t– функционирование транспортной системы рассматриваемого региона в течение наиболее напряженного (установленного) периода времени года. Для любого момента времени ti≠t0ТС может находиться в каждом из пяти дискретных состояний, а вероятность случайного процесса определяется величинами P0(t), P1(t), P2(t), P3(t), P4(t). Для графа состояний ТС приняты следующие состояния:
- ожидаемые условия функционирования (ОУФ) ТС региона – состояние P0(t);
- усложнение ОУФ ТС региона, эквивалентное потери 5 % от расчетного значения располагаемой пропускной способности ТС – состояние P1(t);
- усложнение ОУФ ТС региона, эквивалентное потери 10 % от расчетного значения располагаемой пропускной способности ТС – состояние P2(t);
- усложнение ОУФ ТС региона, эквивалентное потери 25 % от расчетного значения располагаемой пропускной способности ТС – состояние P3(t);
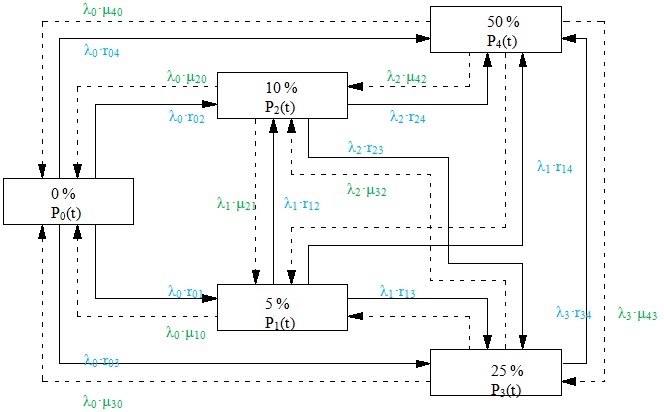
Рис. 2. Граф состояний ТС
Количество состояний графа состояний ТС, равное пяти, представляется рациональным компромиссом между необходимой точностью и сложностью вычислений, необходимых для получения решения задачи.
Система дифференциальных уравнений Колмогорова[3] для графа состояний ТС(см. рис.2) принимает вид:
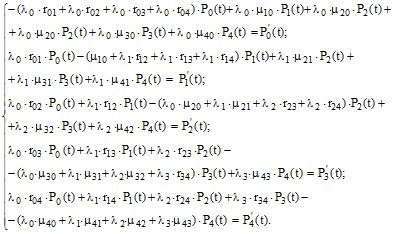 (4)
(4)
Переходные коэффициенты графа состояний ТСвида 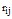 характеризуют способность системы перейти из менее высокого состояния по рангу тяжести в более высокое состояние – происходит уменьшение уровня надежности функционирования ТС.
характеризуют способность системы перейти из менее высокого состояния по рангу тяжести в более высокое состояние – происходит уменьшение уровня надежности функционирования ТС.
Переходные коэффициенты графа состояний ТСвида 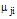 характеризуют способность системы перейти из более высокого состояния по рангу тяжести в менее высокое состояние– происходит увеличение (восстановление) уровня надежности функционирования ТС.
характеризуют способность системы перейти из более высокого состояния по рангу тяжести в менее высокое состояние– происходит увеличение (восстановление) уровня надежности функционирования ТС.
Расчетные значения для интенсивностей (или частоты) отказов основных компонентов ТС региона (см. рис. 1)за период времени в N=30 календарных дней приведены в табл.1.
Таблица 1
Значения интенсивностей отказов основных компонентов ССП
|
Ранг особой ситуации |
Интенсивность отказов основных компонентов ТС, день-1 |
Сумма интенсивностей по рангам ОС |
|||
|
автомобильный транспорт |
железнодорожный транспорт |
воздушный транспорт |
водный транспорт |
||
|
потери пропускной способности 5% |
24/30=8,0×10-1 |
6/30=2,0×10-1 |
16/30=5,33×10-1 |
2/30=6,67×10-2 |
1,60 |
|
потери пропускной способности 10% |
4/30=1,33×10-1 |
2/30=6,67×10-2 |
8/30=2,67×10-1 |
1/30=3,33×10-2 |
0,50 |
|
потери пропускной способности 25% |
2/30=6,67×10-2 |
1/30=3,33×10-2 |
2/30=6,67×10-2 |
0/30=0 |
0,17 |
|
потери пропускной способности 50% |
1/30=3,33×10-2 |
0/30=0 |
1/30=3,33×10-2 |
0/30=0 |
0,07 |
|
Сумма отказов по компонентам ТС |
1,031 |
0,30 |
0,90 |
0,10 |
2,333 |
Данные о парировании особых ситуаций ТС за расчетный период времени представлены в табл.2:
Таблица 2
Значения вероятностей парирования отказов компонентов ТС
|
Ранг особой ситуации |
Общее количество отказов, приведших к возникновению особой ситуации |
Количество парированных отказов |
Условная вероятность парирования отказов |
|
потери пропускной способности 5% |
48 |
21 |
21/48=0,438 |
|
потери пропускной способности 10% |
15 |
9 |
9/15=0,600 |
|
потери пропускной способности 25% |
5 |
2 |
2/5=0,400 |
|
потери пропускной способности 50% |
2 |
1 |
1/2=0,500 |
Результаты расчета вероятности пребывания ТС при воздействии исходных негативных факторов (уровень надежности функционирования ТС) представлены на рис.3-5:
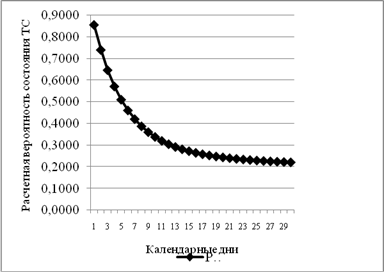
Рис. 3. Распределение вероятности пребывания ТС в принятом состоянии P0(t)
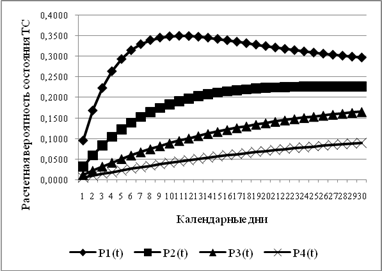
Рис. 4. Распределение вероятности пребывания ТС в принятых состояниях P1(t)÷ P4(t)
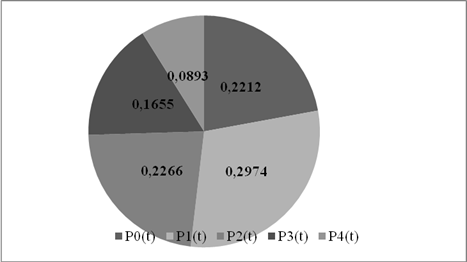
Рис. 5. Распределение вероятности пребывания ТС в состояниях P0(t)÷ P4(t) на последний день (n=30), принятый к анализу
Проверка выполнения обязательного условия (1):
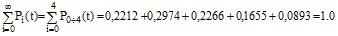 (6)
(6)
Условие выполняется, следовательно, расчет произведен корректно.
Выводы
В работе предложена методика моделирования условий функционирования транспортной системы.
Результаты оценки уровня надежности ТС региона, которая находится под воздействием исходных негативных факторов, приведены в виде распределения вероятностей принятых состояний в течение установленного срока (продолжительности) эксплуатации.
Полученные количественные значения могут рассматриваться в качестве обоснования для принятия решения о соответствии реального уровня надежности функционирования ТС заданным характеристикам.
Рецензенты:
Копнов В.А., д.т.н., профессор, проректор по научной работе ФГАОУ ВПО «Российский государственный профессионально-педагогический университет», г. Екатеринбург.
Баженов Е.Е., д.т.н., профессор, директор ООО «Институт автомобильного транспорта и технических экспертиз», г. Екатеринбург.



