Технические средства обучения (компьютер, Интернет и др.) дают больше возможностей для получения информации и новых знаний, но это не гарантирует их усвоение и применение. Работая с учащимися (студентами и старшеклассниками), всё чаще приходится сталкиваться с отсутствием культуры счёта, в том числе устного, навыков действия с обыкновенными и алгебраическими дробями, что сказывается на дальнейшем процессе обучения в вузе. Если несколько лет назад трудности и ошибки при работе с обыкновенными дробями были у двух-трёх учащихся, то теперь это носит более массовый характер. Рассмотрим ошибки, которые допускают учащиеся.
Обыкновенные дроби
1. При решении систем линейных алгебраических уравнений корни уравнения являются не целыми, а дробными числами, точнее, обыкновенными дробями. Необходимо провести проверку, но вместо обыкновенных дробей учащийся подставляет десятичные дроби, и ответ не сходится на одну сотую. Все вычисления он выполняет на калькуляторе и обыкновенные дроби переводит в десятичные, не понимая, что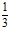 
– это точное значение, а 
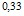– приближенное.
2. При сложении и вычитании правильных дробей допускаются ошибки нескольких видов.
Первая ошибка. Если числители одинаковые, а знаменатели разные, то учащийся складывает знаменатели и оставляет общий числитель:
или 
.
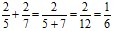Вторая ошибка. Если числители и знаменатели разные, то учащийся складывает числитель с числителем, знаменатель со знаменателем:
.
Полученный ответ не вызывает ни каких сомнений в правильности вычислений у учащегося. Правило сложения обыкновенных дробей с разными знаменателями для него не существует.
3. Не каждую обыкновенную дробь можно перевести в конечную десятичную дробь. Решая примеры (или второпях, или по невниманию, или по незнанию), учащийся может записать: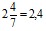 
.
Другой пример. Смешанное число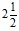 
воспринимают как произведение 
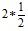и сокращают выражение 
.
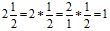4. Перевод смешанного числа в неправильную дробь.
Представить смешанное число 
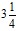в виде неправильной дроби. Ход преобразования учащегося: 
.
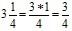5. Сложение (вычитание) смешанных чисел.
При сложении число переводят в неправильную дробь, после этого приводят к общему знаменателю, складывают и затем выделяют целую часть. В ходе таких преобразований допускают ряд ошибок:
.
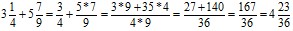Алгебраические дроби
Ещё большего удивления вызывают действия с алгебраическими дробями и их преобразования учащимися. Известно, что каждое слагаемое в числителе можно поделить на знаменатель: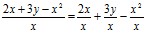 
. По аналогии числитель делят на каждое слагаемое в знаменателе: 
.
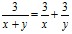При сложении алгебраических дробей также складывают знаменатель со знаменателем, числитель с числителем, но ещё большее удивление вызывает преобразование и сокращение алгебраической дроби:
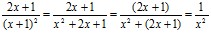или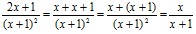 
,
т.е. числитель и знаменатель сократили на слагаемое, и в результате «двух разных» способов преобразования получены разные ответы.
Если имеем дробное выражение, содержащее элементарные функции, то здесь учащиеся позволяют себе ещё больше вольностей в преобразовании выражения, при этом аргумент функции воспринимают как множитель:
.
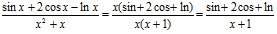Вычисление арифметического корня
При вычислении корня из суммы пишут сумму корней:
, 
.
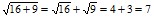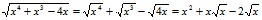Если просишь объяснить ход вычисления, то получаешь такой ответ: «Корень из произведения равен произведению корней, извлекаем корень из каждого множителя и результат перемножаем. Аналогично извлекаем сумму корней – корень из суммы равен сумме корней». Приходится объяснять, что при извлечении корня из суммы числовое выражение складываем, а потом извлекаем корень из полученного числа: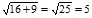 
, В алгебраическом выражении извлекать корень из каждого слагаемого в отдельности нельзя.
Вычислительная культура, в частности культура устного счёта, у современных учащихся очень низка. Умножение нескольких однозначных чисел многие выполняют на калькуляторе, не давая себе труда вычислить это устно. Умножение и деление многозначных чисел столбиком – анахронизм, недостойный внимания. Навыки счёта, в том числе устного, сказываются на восприятии и скорости усвоения новых математических знаний.
Студентам первого курса был дан тестовый пример:
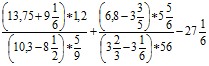
В тестировании принимали участие студенты первого курса набора 2011 года шести инженерных специальностей, в количестве 148 человек. Проверялись правильность и скорость решения. Результаты сравнивали с показателями 2001 года, опрошено 161 человек.
Таблица 1
Количество правильных ответов
|
Год |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
Кальку-лятор |
|
2011 |
45 |
2 |
5 |
7 |
13 |
11 |
12 |
14 |
11 |
14 |
0 |
0 |
9 |
5 |
|
2001 |
126 |
9 |
14 |
12 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Наглядно ухудшение качества вычислительных навыков представлено на рис. 1 и 2.
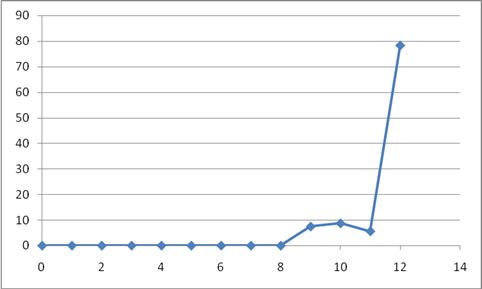
Рис. 1. Уровень выработки вычислительного навыка в 2001 году (горизонтальная ось – оценка по 12-балльной шкале, вертикальная ось – процент тестируемых с соответствующей оценкой).
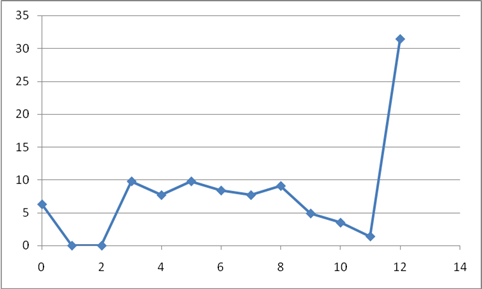
Рис. 2. Уровень выработки вычислительного навыка в 2011 году (горизонтальная ось – оценка по 12-балльной шкале, вертикальная ось – процент тестируемых с соответствующей оценкой).
На калькуляторе пример решали 3,38% (5 человек). Среди тех, кто выполнил не более пяти действий - 32,43% (48 человек), происходит основной отсев студентов: в течение первого семестра забирают документы 20,83% (10 человек), после первой сессии 14,58% (7 человек), в течение второго семестра 16,67% (8 человек), всего 52,08% (25 человек), или 16,89% от общего числа тестируемых студентов. В течение третьего семестра и после его окончания 22,91% (11 человек). Итого за три семестра убыло 75% (36 человек из 48), или 24,32% от общего числа студентов (36 из 148).
Правильно решили пример в 2011 году 30,4% (45 человек), в 2001 году – 78,26% (126 человек). В 2011 году из 148 тестируемых 112 студентов (75,68%) продолжили учёбу. Все тестируемые в 2001 году закончили своё обучение.
Таблица 2
Время, затраченное на решение примера (в минутах).
|
Год |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
2011 |
2 |
8 |
12 |
16 |
19 |
17 |
16 |
14 |
15 |
12 |
8 |
9 |
|
2001 |
15 |
31 |
32 |
38 |
29 |
11 |
5 |
0 |
0 |
0 |
0 |
0 |
Возросло время: больше 10 минут пример решало 44,59% (66 человек). Увеличилось время решения примера, т.е. среднее время в 2011 году 8,34 минуты, в 2001 – 6,55 минуты, временные затраты выросли на 27,33%. Это в свою очередь сказывается на количестве задач, которые студенты успевают разобрать и решить в аудитории – в среднем на 30% меньше, чем в 2001 году. При выполнении контрольных и самостоятельных работ в аудитории объём решённых заданий за отведённое время сократился на 35%.
Необходимо отличать студентов, которые выполняют задание медленно, аккуратно, грамотно с развёрнутым решением и нестандартным подходом, от тех, кто решает долго и с ошибками, неразборчиво и грязно. В первом случае таких студентов в группе бывает от одного до трёх человек.
Данное тестирование выявило, что утраченные навыки культуры устного счёта сказываются на качестве процесса обучения – на скорости восприятия информации, её переработке и усвоении.
На рис. 3 приведена графическая зависимость вероятности отчисления на первых-вторых курсах от уровня вычислительного навыка по выборке из 300 студентов. Уровень выработки вычислительного навыка оценен по 12-балльной шкале.
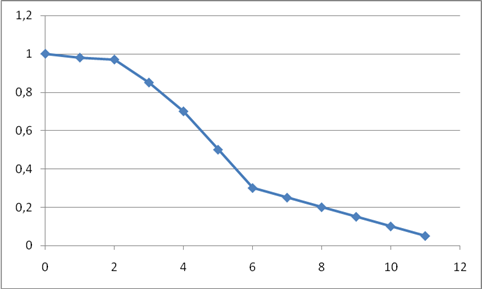
Рис. 3. Вероятность отчисления студентов 1, 2-го курсов в зависимости от уровня выработки вычислительных навыков.
В моей педагогической практике не раз встречались студенты с прекрасными вычислительными навыками и культурой счёта, которые выполняли расчёты с точностью до пяти знаков после запятой, не используя вычислительную технику, быстрее тех, кто все вычисления производил на калькуляторе. Среди студентов с высокой культурой вычисления были выпускники из городских и сельских школ, они успешно учились в вузе и заканчивали его, как правило, с отличием.
К сожалению, культура счёта (как и любая культура чтения, письма и т.д.), не привитая в своё время, невосполнима и сужает горизонты возможностей познания и реализации себя в будущем студента как человека и личности, как грамотного и творческого специалиста.
Рецензенты:
Абдуллаев А.Р., д.ф.-м.н., профессор кафедры высшей математики ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.
Цаплин А.И., д.т.н., профессор кафедры общей физики ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.