Введение. Перфорация скважин широко применяется и для дополнительного вскрытия пластов (дострелов) в целях восстановления или повышения добычи, при переходе на эксплуатацию вышележащих горизонтов, а также при солянокислотной обработке и другим методам воздействия на прискважинную зону. Качественное вскрытие пластов перфорацией имеет важное, а подчас решающее значение для правильной оценки продуктивности разведочных скважин и осуществления максимально возможной отдачи продуктивных пластов, сокращения сроков сооружения и освоения скважин, эффективного использования скважины в течение долгих лет ее эксплуатации [3].
После вскрытия пласта возникает задача определения качества перфорации. Представляется, что одним из эффективных способов оперативного контроля качества вскрытия пласта перфорацией (оценка длины перфорационных каналов) могут быть акустические методы, связанные с особенностями эволюции волн, распространяющихся по жидкости внутри перфорированной скважины [4, 7, 11].
В [9, 14] волновой метод используется для оценки коллекторских характеристик призабойной зоны временно остановленных нефтяных и газовых скважин. Использование волн с целью очистки и исследования призабойной зоны нефтяных скважин рассмотрено в [1, 5, 6, 12, 15,16]. Процесс распространения одномерных монохроматических волн в пористой среде, насыщенной газом, исследуется в [2, 8, 10, 13].
В работе исследовано распространение гармонических волн в перфорированном и непроницаемом (не перфорированном) участках заполненной жидкостью и окруженной проницаемой пористой средой скважины. Изучено влияние коллекторских характеристик пористой среды окружающей скважину и длины перфорационных каналов на эволюцию гармонических волн, распространяющихся в перфорированном участке скважины.
1. Основные уравнения. Рассмотрим перфорированную скважину, окруженную насыщенной жидкостью проницаемой пористой средой. Для описания распространения гармонических волн в перфорированном участке скважины примем следующие допущения: образовавшиеся перфорационные каналы на поверхности скважины расположены равномерно с плотностью n на единицу площади и имеют одинаковые длину l и радиус b.
Будем полагать, что волна распространяется вдоль оси скважины, а длина волновых возмущений λ значительно меньше длины перфорированного участка L и больше радиуса скважины a, а также больше расстояния между двумя соседними перфорационными каналами.
Пусть в сечении скважины на границе раздела участков с непроницаемыми (первая зона) и перфорированными (вторая зона) стенками длиной H и L соответственно акустические свойства системы изменяются скачкообразно. Ось z расположена параллельно оси скважины, при этом граница раздела находится в сечении с координатой z=0.
В рамках модели плоского движения нестационарное течение жидкости в скважине при распространении возмущений будем описывать в квазиодномерном приближении. В первой зоне возмущение давления и скорость жидкости удовлетворяют уравнениям неразрывности и импульсов:
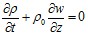 , (1)
, (1)
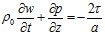 . (2)
. (2)
Здесь 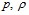 – возмущения давления и плотности жидкости соответственно,
– возмущения давления и плотности жидкости соответственно, 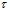 – вязкое напряжение на внутренней поверхности стенки скважины.
– вязкое напряжение на внутренней поверхности стенки скважины.
Для перфорированного участка скважины (вторая зона) уравнения неразрывности и импульса имеют вид:
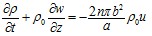 , (3)
, (3)
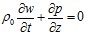 . (4)
. (4)
Здесь 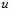 – скорость утечки (или притока) жидкости из скважины в перфорационные каналы. Так как во второй зоне эволюция волны в основном определяется эффектами фильтрации жидкости из перфорационных каналов в окружающее пористое пространство, то в уравнении импульса действием вязкостных напряжений можно пренебрегать. Правая часть уравнения неразрывности описывает процесс утечки (или притока) жидкости из скважины через перфорационные каналы при распространении волн.
– скорость утечки (или притока) жидкости из скважины в перфорационные каналы. Так как во второй зоне эволюция волны в основном определяется эффектами фильтрации жидкости из перфорационных каналов в окружающее пористое пространство, то в уравнении импульса действием вязкостных напряжений можно пренебрегать. Правая часть уравнения неразрывности описывает процесс утечки (или притока) жидкости из скважины через перфорационные каналы при распространении волн.
Для определения скорости 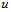 запишем уравнение сохранения массы жидкости внутри перфорационного канала:
запишем уравнение сохранения массы жидкости внутри перфорационного канала:
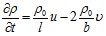 . (5)
. (5)
На основе решения внешней фильтрационной задачи определим скорость фильтрации флюида через стенки перфорационного канала 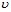 . Для определения поля давления вокруг перфорационного канала используем уравнение пьезопроводности:
. Для определения поля давления вокруг перфорационного канала используем уравнение пьезопроводности:
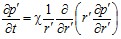 ,
, 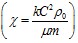 . (6)
. (6)
Здесь 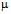 – вязкость жидкости;
– вязкость жидкости; 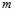 ,
, 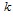 – коэффициенты пористости и проницаемости окружающей скважины пористой среды соответственно;
– коэффициенты пористости и проницаемости окружающей скважины пористой среды соответственно; 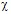 – коэффициент пьезопроводности;
– коэффициент пьезопроводности; 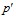 – распределение давления вокруг канала;
– распределение давления вокруг канала; 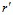 – радиальная координата.
– радиальная координата.
Фильтрацию жидкости из перфорационных каналов в окружающую пористую среду опишем с помощью закона Дарси:
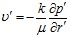 , (7)
, (7)
где 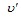 – распределение скорости фильтрации жидкости вокруг перфорационного канала.
– распределение скорости фильтрации жидкости вокруг перфорационного канала.
Используя условие непрерывности скорости и давления на границе 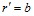 , для уравнений (6), (7) запишем следующие граничные условия:
, для уравнений (6), (7) запишем следующие граничные условия:
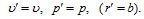 (8)
(8)
Для второго граничного условия для уравнения пьезопроводности (6) рассмотрим два предельных случая: а) глубина проникания волн давления 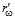 меньше среднего расстояния между соседними перфорационными каналами
меньше среднего расстояния между соседними перфорационными каналами 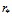 , и, следовательно, фильтрационные потоки жидкости из двух соседних перфорационных каналов слабо взаимодействуют между собой; б) величина
, и, следовательно, фильтрационные потоки жидкости из двух соседних перфорационных каналов слабо взаимодействуют между собой; б) величина 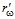 сравнима с величиной
сравнима с величиной 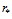 или превышает ее. Будем полагать, что вокруг соседних перфорационных каналов имеются одинаковые поля давления, и фильтрация жидкости через границу между соседними перфорационными каналами отсутствует. Для этих случаев граничные условия можно записать в виде:
или превышает ее. Будем полагать, что вокруг соседних перфорационных каналов имеются одинаковые поля давления, и фильтрация жидкости через границу между соседними перфорационными каналами отсутствует. Для этих случаев граничные условия можно записать в виде:
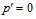 ,
, 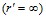 (9 а)
(9 а)
или
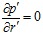 ,
, 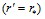 . (9 б)
. (9 б)
В качестве величины 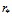 примем половину среднего расстояния между основаниями перфорационных каналов на поверхности скважины.
примем половину среднего расстояния между основаниями перфорационных каналов на поверхности скважины.
Уравнение состояния жидкости запишем в виде:
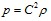 . (10)
. (10)
Здесь 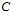 – скорость звука в жидкости.
– скорость звука в жидкости.
2. Распространение гармонических волн в перфорированном участке. Пусть гармоническая волна падает по направлению нормали к плоской границе раздела. Тогда движение в непроницаемой зоне определяется наложением двух волн: падающей и отраженной. В перфорированной зоне имеется только прошедшая волна. Для описания распространения этих волн получены волновые числа для непроницаемой (первой) и перфорированной (второй) зон.
Для непроницаемой зоны волновое число имеет вид:
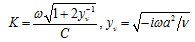 , (11)
, (11)
а для перфорированного участка
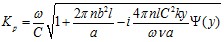 . (12)
. (12)
Здесь 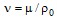 – кинематическая вязкость жидкости. В зависимости от граничных условий (9 а) и (9 б) функция
– кинематическая вязкость жидкости. В зависимости от граничных условий (9 а) и (9 б) функция 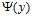 определяется соответственно по формулам:
определяется соответственно по формулам:
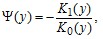 (13 а)
(13 а)
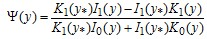 . (13 б)
. (13 б)
Здесь 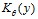 – функция Макдональда,
– функция Макдональда, 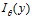 – модифицированная функция Бесселя первого рода порядка
– модифицированная функция Бесселя первого рода порядка 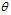 .
.
Из выражения (12) следует, что волновое число зависит от параметров скважины, жидкости, а также от величин 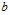 ,
, 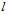 ,
, 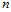 , определяющих качество вскрытия пласта перфорацией. При этом радиус перфорационных каналов определяется размером пуль, а их плотность – типом перфоратора [3]. Следовательно, неизвестной величиной, от которой зависит качество вскрытия, является длина перфорационных каналов
, определяющих качество вскрытия пласта перфорацией. При этом радиус перфорационных каналов определяется размером пуль, а их плотность – типом перфоратора [3]. Следовательно, неизвестной величиной, от которой зависит качество вскрытия, является длина перфорационных каналов 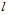 .
.
Фазовая скорость 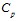 и коэффициент затухания
и коэффициент затухания 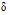 волн давления определяются по формулам
волн давления определяются по формулам 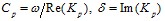 . На рис. 1, 2 показаны зависимости фазовой скорости
. На рис. 1, 2 показаны зависимости фазовой скорости 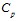 и коэффициента затухания
и коэффициента затухания 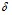 акустических возмущений от частоты для перфорированного участка скважины, окруженного проницаемой пористой средой. При низких частотах
акустических возмущений от частоты для перфорированного участка скважины, окруженного проницаемой пористой средой. При низких частотах 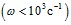 , как коэффициент затухания, так и фазовая скорость, полученные с использованием граничных условиях (9 а), (9 б), значительно отличаются друг от друга. Сравнение линий 1 и 2 показывает, что увеличение длины перфорационного канала
, как коэффициент затухания, так и фазовая скорость, полученные с использованием граничных условиях (9 а), (9 б), значительно отличаются друг от друга. Сравнение линий 1 и 2 показывает, что увеличение длины перфорационного канала 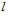 в три раза приводит к аналогичному увеличению коэффициента затухания.
в три раза приводит к аналогичному увеличению коэффициента затухания.
Для высокочастотных волн 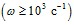 глубина проникания волн меньше чем
глубина проникания волн меньше чем  , поэтому результаты, полученные при граничных условиях (9 а), (9 б), практически совпадают.
, поэтому результаты, полученные при граничных условиях (9 а), (9 б), практически совпадают.
Также видно, что с уменьшением коэффициента проницаемости пористой среды уменьшается также коэффициент затухания.
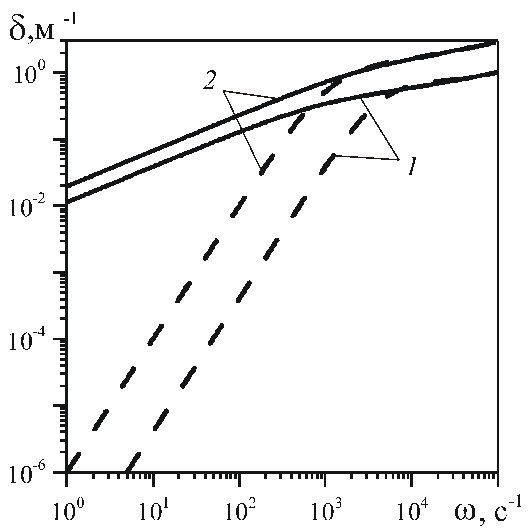
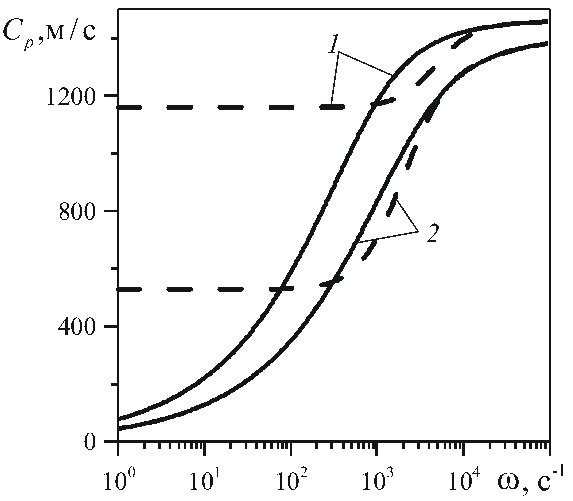
Рис. 1. Влияние длины перфорационного канала (1 – 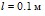 , 2 –
, 2 – 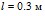 ) на коэффициент затухания
) на коэффициент затухания  и фазовую скорость
и фазовую скорость 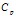 в перфорированном участке скважины, окруженной высокопроницаемой пористой средой (
в перфорированном участке скважины, окруженной высокопроницаемой пористой средой (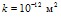 ). Сплошные линии соответствуют решению с использованием граничного условия (9 а), а штриховые – с использованием граничного условия (9 б)
). Сплошные линии соответствуют решению с использованием граничного условия (9 а), а штриховые – с использованием граничного условия (9 б)
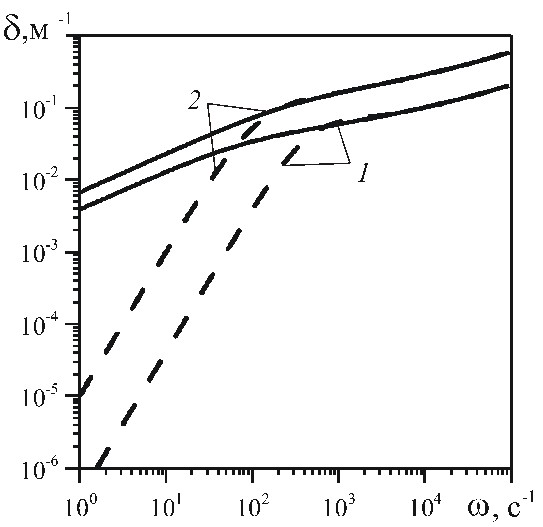
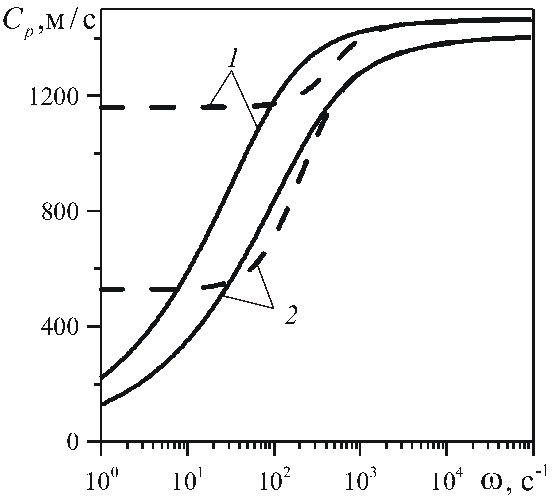
Рис. 2. Зависимости коэффициента затухания и фазовой скорости возмущений от частоты в перфорированном участке скважины, окруженной низкопроницаемой пористой средой (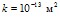 ). Обозначения линий такие же, как на рис. 1
). Обозначения линий такие же, как на рис. 1
Вывод. Поскольку коэффициент затухания и фазовая скорость волны в перфорированном участке сильно зависят от длины перфорационного канала, от которой зависит качество вскрытия скважины перфорацией, то полученные результаты дают основание делать вывод о возможности использования акустического метода для экспресс-контроля качества вскрытия перфорацией скважины.
Работа выполнена при поддержке гранта СФ БашГУ № В14-19.
Рецензенты:
Мустафина С.А., д.ф.-м.н., профессор кафедры математического моделирования, Стерлитамакский филиал ФГБОУ ВПО «Башкирский государственный университет», Республика Башкортостан, г. Стерлитамак;
Михайлов П.Н., д.ф.-м.н., профессор кафедры алгебры, геометрии и методики обучения математике, Стерлитамакский филиал ФГБОУ ВПО «Башкирский государственный университет», Республика Башкортостан, г. Стерлитамак.



