Графическая подготовка специалистов и бакалавров технического профиля остается одним из актуальных направлений обучения, необходимым условием формирования профессиональных компетенций, связанных с оформлением технической документации, без которой невозможно организовать процесс производства, эксплуатации и ремонта любого механизма, машины, устройства или сооружения. Формой контроля и средством формирования графических способностей обучаемых являются графические задачи, в составе которых мы рассмотрели компоненты: задачную и решающую системы, и провели сравнительный анализ решения применяемых нами творческих витагенно-ориентированных задач, с классическими графическими задачами и графическими задачами с материальными объектами [5].
В задачностную систему, по мнению ряда исследователей [1], входят предмет, условия и требования задачи, решающая система включает в себя набор взаимосвязанных методов, способов и средств решения задачи. Решающая система графических задач состоит из определенной последовательности действий, производимых при решении различных графических задач. Рассмотренный ранее сравнительный анализ [5] графических действий позволяет определить преимущества и недостатки процесса графической подготовки классического и витагенно-ориентированного содержания. Дальнейшие изыскания в этом направлении состоят в определении и сравнительном анализе применяемых при решении графических задач различных видов операций, методов и средств. Ранее нами были рассмотрены следующие виды графических задач: классическая графическая задача, графическая задача с материализованным объектами и творческая витагенно-ориентированная графическая задача. Действия, выполняемые обучаемыми при решении вышеперечисленных задач, приведены в таблице 1.
Таблица 1
|
Классическая графическая задача, графическая задача с материализованными объектами |
Творческая витагенно-ориентированная графическая задача |
|
Действия (ознакомление, перевод данных в графическую форму, визуализация данных, составление плана, осуществление решения, графическое оформление, анализ решения) |
Действия (ознакомление, материализация объекта, подбор сюжета, визуализация данных, формулировка задачи, перевод данных в графическую форму, составление плана, осуществление решения, графическое оформление, анализ решения, корректировка условия, осуществление решения) |
Выполнение каждого из вышеперечисленных действий требует проектирования их составляющих, диагностики возможных проблем при их выполнении, разработки их методической основы. Методику рассматривают как фиксированную совокупность приемов практической деятельности, приводящей к заранее определенному результату [3]. Методическая составляющая решения графических задач относится к специфической сфере научной деятельности: теории и методики обучения общепрофессиональным (общетехническим) дисциплинам, в частности к планированию и организации процесса графической подготовки. Конкретизируя методы, применяемые при выполнении того или иного действия в решении графической задачи, мы рассматриваем метод как совокупность приемов и операций познания и практического преобразования действительности; способ достижения определенных результатов в познании и практике [2], детализируем действия, производимые в процессе решения графических задач с учетом их методической основы.
Поскольку действия по решению классических задач и задач с материализованными объектами совпадают, ограничимся сравнением методов, применяемых при решении задач классических и творческих витагенно-ориентированных графических задач (табл. 2).
Таблица 2
|
Методика решения графических задач |
|
|
Классическая графическая задача. |
Творческая витагенно-ориентированная графическая задача. |
|
Построить проекции прямой линии CD, скрещивающейся с прямой AB, если координаты точек следующие: A (XA=10; YA=10; ZA=15), B (XB=60; YB=50; ZB=45), C (XC=55; YC=10; ZC=5), D (XD=30; YD=?; ZD=?), а прямая CD расположена выше прямой AB на 10 мм в точке, которая является серединой прямой AB. |
Изучите тему: «Взаимное положение прямых в пространстве», рассмотрите варианты решения задач на построение параллельных пересекающихся и скрещивающихся прямых. Используя материальные аналоги прямой линии (любые материальные прямые), составьте и решите задачу на заданную тему. Графическое условие задачи и ее решение оформите с применением правил построения чертежа. |
|
1. Ознакомление |
|
|
Чтение данных, условия задачи и требований. |
Чтение данных, условия задачи и требований. |
|
Изучение данных. Чтение условия задачи, определение положения заданных точек на эпюре по координатам точек. Отбор основных и второстепенных условий. Основные условия: взаимное положение заданных прямых (скрещивающиеся); положение точек. Второстепенные, но однозначно определяющие решение условия: определение проекций точки – середина прямой AB. Определение логики учебного материала. Даны две проекции прямой AB, две проекции точки C и координата X точки D. Можно найти середину отрезка AB, точку, лежащую на 10 мм выше этой точки, и, таким образом, найти искомую прямую по двум принадлежащим ей точкам. |
Изучение данных. Чтение условия задачи. Отбор основных и второстепенных условий. Основные условия: Тема для изучения: «Взаимное положение прямых в пространстве». Постановка проблемы: используя материальные аналоги прямой линии (любые материальные прямые), составить и решить задачу на заданную тему. Второстепенные условия (подсказка): рассмотрите варианты решения задач на построение параллельных пересекающихся и скрещивающихся прямых. Графическое условие задачи и ее решение оформить с применением правил построения чертежа. Определение логики учебного материала. Даны темы для рассмотрения и типы аналогичных задач. Необходимо выбрать вид прямых (скрещивающиеся), подобрать их материальные аналоги и осуществить постановку проблемы (для чего нужно решить задачу?). Анализ задач классического содержания на данную тему. Анализ задач на построение скрещивающихся прямых. |
|
Перевод данных в графическую форму |
|
|
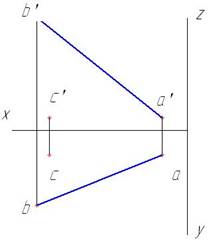
Метод параллельного проецирования: 1) построение проекций точек по координатам или заданным размерам на эпюре (изображение, полученное методом параллельного, ортогонального проецирования). В зависимости от условия задачи применимы и другие методы получения графических изображений: метод центрального проецирования, метод аффинного преобразования; 2) соединение точек для получения заданной прямой AB (рис. 1). Создание изображения предполагает следующие способы: черчение ручными средствами (карандаш, линейка, ватман и т д); выполнение электронного чертежа, что мы и применили при помощи компьютерной программы «Компас».
Рис. 1. Графическое условие задачи классического содержания. |
|
|
Материализация объектов |
|
|
Подбор материальных предметов, имеющих сходство с объектами задачи; метод аналогии: поиск предметной аналогии, то есть материального предмета, имеющего форму прямой или, в нашем случае, двух скрещивающихся прямых. При возникновении затруднений с целью дополнительной мотивации процесса возможно применение методов активизации мышления: - мозговой штурм; - метод фокальных объектов; - синектика; - метод контрольных вопросов. Например, проведение мозгового штурма на тему: найти аналог понятию «прямая» − некий объект реального мира, представляющий собой прямую линию, длина которой намного больше размеров поперечного сечения. Основное свойство прямой линии − отсутствие толщины и ширины [ссылка на монографию]. Результат проведения мозгового штурма со студентами первого курса технических специальностей В качестве прямой линии могут быть использованы следующие объекты: струна на гитаре, стрелка на циферблате, плинтус, ракета на старте, стержень в ручке, топор, рельс, шпала, ступица в колесе, змея на дереве, туннель, цепь, весло у гребца, растяжка к мине в зоне боевых действий, шлагбаум на дороге, рельсы и шпалы, рельсы и контактная сеть. |
|
|
Визуализация данных |
|
|
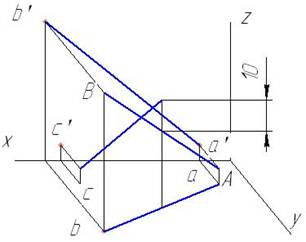
Чтение эпюра (чертежа) условия задачи – на эпюре представлены горизонтальная и фронтальная проекции прямой AB и точки C. Создание пространственного образа данных: представление (репрезентация) плоского изображения эпюра в объемные образы, анализ плоского изображения с целью определения местоположения прямой и точки относительно плоскостей проекций. На горизонтальной и фронтальной проекции точка a находится ближе к оси X, следовательно, прямая AB - нисходящая прямая общего положения. Точка C находится ближе во фронтальной и горизонтальной плоскости, чем точка B. Поиск пространственного решения задачи: исходя из пространственных представлений прямой AB и точки C решение задачи - это прямая общего положения, соединяющая точку C и точку, лежащую выше на 10 мм середины прямой AB (рис. 2).
Рис. 2. Пространственное представление условия задачи и поиска решения. |
|
|
Подбор сюжета (используемые методы) |
|
|
Перебор ситуаций: жизненного опыта (витагенная информация); производственной технической; исторических фактов; знаний из других областей (география, биология, химия, физика, литературные источники; фольклорные сюжеты. Для составления задачи выбраны материальные аналоги скрещивающихся прямых линий: рельсы и контактная сеть. Провод контактной сети и рельсы, вопреки распространенному представлению об их параллельности, на прямом отрезке пути представляют скрещивающиеся прямые линии (информация, полученная студентом железнодорожного вуза из вводного профессионально ориентированного курса «Общий курс железных дорог»). Для формулировки условий задачи необходимо задать размеры объектов: высота провода - 6800 мм, расстояние между рельсами - 1524 мм. |
|
|
Визуализация данных |
|
|
Создание пространственного образа данных. Этот этап решения задачи менее сложен для студентов. Образы материальных аналогов скрещивающихся прямых (рельсы и контактная сеть) понятны и доступны воображению обучаемого. Поиск пространственного решения задачи. Обучаемый создает пространственные представления: рельсы и контактная сеть – они не параллельны, и угол скрещивания не может быть большим (±3°). Условно, для усиления наглядности чертежа, возможно увеличение угла до 10°. Если ось рельса параллельна плоскости H и V, то задача решается элементарно. Поэтому для усложнения условия можно задать угол между осью рельса и плоскостью V или H. Наклон полотна (оси рельса) к плоскости H потребует введения дополнительных плоскостей проекций (новой фронтальной проекции V1) для построения скрещивающейся контактной сети, поэтому рациональней задать угол наклона оси рельса к плоскости V. |
|
|
Составление плана решения задачи |
|
|
Формулировка проблемы: построить эпюр заданных скрещивающихся прямых. Анализ данных условия задачи Дана прямая AB в проекциях согласно свойствам параллельного проецирования - проекции точки - середины прямой линии находятся посередине соответствующих проекций прямой. 10 мм – увеличение координаты z по отношению к точке середине прямой AB. Поиск решения: Прямая CD проходит через точку E с координатами XE= (XA+XB)/2=35; YE=(YA+YB)/2=30; ZE=(ZA+ZB)/2+10=40. Построить точку E, соединить с точкой C. Продлить до вертикальной прямой с координатой X=30. В процессе поиска решения был применен известный алгоритм построения скрещивающихся прямых и введена дополнительная точка Е. При поиске решения возможно применение следующих методов решения графических задач: применение известных алгоритмов; преобразование условий задачи (введение дополнительных объектов); изменение данных, удаление лишних данных; разработка нового алгоритма (логического построения) решения задачи. Перебор вариантов решения Решение имеет одни вариант. Построение структуры решения Решение в три этапа Планирование этапов решения 1. Построение точки E. 2. Построение прямой CE. 3. Построение точки D. |
|
|
Формулировка задачи |
|
|
Разработка текста задачи – текст должен содержать все условия и данные, необходимые для решения задачи. Анализ данных – с целью оценки решаемости задачи. Построить эпюр провода и рельс, если известны: высота провода - 6800 мм, расстояние между рельсами - 1524 мм. Задать угол наклона оси пути к плоскости V - 45°, а угол, который горизонтальная проекция провода образует с горизонтальной проекцией рельса, − 10°. (ссылка на сборник). Построение изображения как заданное условие задачи. В данном случае нет в этом необходимости. Текст содержит все данные. |
|
|
Перевод данных в графическую форму |
|
|
В данном случае в этом нет необходимости, поскольку построение эпюра заданных объектов и является решением задачи. Если в условии задачи заданы объекты, имеющие координаты или часть данных, которые необходимо представить в графической форме для решения задачи, то тогда применяются следующие методы: метод параллельного проецирования; метод центрального проецирования; метод аффинного преобразования. |
|
|
Осуществление решения: |
|
|
1. Графическое построение – дополнительное построение (точка, прямая, плоскость, линии уровня, параллельные объекты, перпендикуляры). В данном случае строим дополнительную точку E и через нее и заданную точку C проводим искомую прямую. При осуществлении решения возможно применение следующих методов решения графических задач: метод преобразования чертежа (замена плоскостей проекций, вращения, плоскопараллельного перемещения); родственные преобразования. 2. Аналитическое решение (математический расчет). 3. Комбинированный. |
|
|
Составление плана решения задачи |
|
|
Формулировка проблемы: построить эпюр заданных скрещивающихся прямых. Анализ данных условия задачи. Даны две прямые: рельсы условно принимаем лежащими на горизонтальной плоскости проекций, и контактная сеть, поднятая на высоту 6800 м. Поиск решения: применение известных алгоритмов; преобразование условий задачи (введение дополнительных объектов); изменение данных, удаление лишних данных; разработка нового алгоритма (логического построения) решения задачи. В данном случае применим известный алгоритм решения задач на построение скрещивающихся прямых в соответствии с заданными размерами. Перебор вариантов решения. Решение имеет один вариант. Построение структуры решения. Решение в четыре этапа. Планирование этапов решения. 1. Построение горизонтальной проекции прямой AB – ab рельса под углом 45° к оси X. 2. Построение фронтальной проекции прямой AB – a'b' рельса, совпадающей с осью X. 3. Построение горизонтальной проекции прямой CD – cd контактной сети под углом 10° к горизонтальной проекции прямой AB. 4. Построение фронтальной проекции прямой CD – c'd' контактной сети на высоте 6800 над осью X. |
|
|
Графическое оформление |
|
|
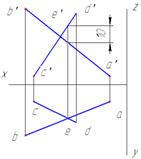
Получение изображений Метод параллельного проецирования - изображение решения, разработанного на предыдущей стадии, на эпюре с применением ортогонального проецирования. При необходимости применяются: метод центрального проецирования; метод аффинного преобразования. Создание изображений Изображение выполнено при помощи компьютерных технологий с применением электронного чертежа (рис. 3).
Рис. 3. Решение задачи. Также возможно выполнение изображений ручным способом, описанным выше: черчение ручным способом |
|
|
Анализ решения |
Осуществление решения |
|
1. Оценка соответствия результатов требованиям: решение соответствует условиям задачи. 2. Оценка правильности и точности решения: построение выполнено по размерам, прямые скрещиваются, точка прямой CD находится посередине прямой AB на 10 мм выше. 3. Качество графического изображения – изображение выполнено в соответствии с Единой системой конструкторской документации. Вывод о необходимости корректировки решения: корректировка решения не требуется. |
В нашем случае графическое построение в масштабе 1:100 по плану. Также возможно: 1. Графическое построение - дополнительное построение (точка, прямая, плоскость, линии уровня, параллельные объекты, перпендикуляры); использование методов преобразования чертежа (замена плоскостей проекций, вращения, плоскопараллельного перемещения); аффинные (родственные) преобразования. 2. Аналитическое решение (математический расчет). 3. Комбинированный метод – совместное применение графического и вычислительного метода решения задачи. |
|
Решение классической задачи завершено. |
|
|
Рассмотрим дальнейшие этапы решения творческой витагенно-ориентированной графической задачи. |
|
|
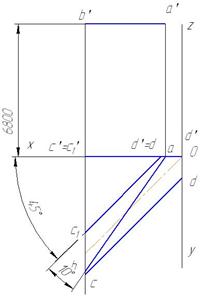
Метод параллельного проецирования - изображение решения, разработанного на предыдущей стадии, на эпюре с применением ортогонального проецирования. При необходимости применяются: метод центрального проецирования; метод аффинного преобразования. Создание изображений Изображение выполнено при помощи компьютерных технологий с применением электронного чертежа (рис. 4). Прямая AB - участок контактной сети. Прямая CD изображает рельс. Также возможно выполнение изображений ручным способом, описанным выше: черчение ручным способом.
Рис. 4. Участок рельса и контактной сети. |
|
|
Анализ решения |
|
Вывод о необходимости корректировки решения: корректировка решения не требуется и проведение последующих этапов. |
|
Сравним методику решения графических задач классического содержания и творческих витагенно-ориентированных задач:
На этапах решения задач различных видов, содержание которых совпадает, методика решения графических задач различных видов не отличается; как правило, это действия, способы и приемы, совершаемые при решении классической графической задачи. Решение классической графической задачи с материализованными объектами является неотъемлемой частью творческой витагенно-ориентированной задачи. Классическая задача по начертательной геометрии с материализованными объектами – это авторский продукт, разработанный студентом в процессе выполнения задания по решению творческой витагенно-ориентированной задачи.
Материализация объекта, подбор сюжета, формулировка задачи - действия, совершаемые исключительно при решении творческой витагенно-ориентированной задачи. Методика выполнения этих действий отличается новизной. На этапе материализации объекта происходит подбор материальных аналогов классическим объектам начертательной геометрии, источником которых является жизненный опыт студентов. С целью стимулирования деятельности студентов на данном этапе решения задачи применимы методы активизации мышления.
На этапе подбора сюжета осуществляется подбор жизненных ситуаций, которые составляют основу задачи. Эти этапы связаны между собой, поскольку чаще всего выбор объектов уже предполагает сформированный сюжет задачи. Разделение этих этапов условно. Методика их реализации взаимозаменяема, методы активизации мышления применимы на каждом из этих этапов, равно как и анализ информации, полученной из различных сфер человеческой деятельности, которая представляет витагенную информацию студента.
Этап формулировки задачи, состоящий в разработке текста задачи, требует проведения анализа данных на предмет их необходимости и достаточности. Выполнение этого этапа требует от студента сформированных представлений о ходе решения разрабатываемой задачи. Методика этого этапа двуедина и сочетает правила написания научно-художественного или художественного текста с научно-графическим анализом его информационного содержания.
Наличие дополнительных этапов с инновационными подходами к теории классической графической дисциплины усложняет процесс применения графически знаний и одновременно создает условия дополнительной мотивации графического обучения, состоящий в разработке и решении авторского продукта студента. Мотивационно-творческая активность графической учебной деятельности студентов, стимулируемая применением творческих витагенно-ориентированных задач, повышает качество графической подготовки.
Решение классической графической задачи вызывает у студентов определенные трудности, вызванные абстрактностью учебного материала начертательной геометрии, которую снижают применением материализованных объектов [4; 6]. Классическая графическая задача как способ применения графических знаний является обязательным этапом решения творческой витагенно-ориентированной задачи. Анализ решения классической графической задачи необходим для творческого применения графических знаний в учебной деятельности, осуществляемого при выполнении творческой витагенно-ориентированной задачи.
Сравнительный анализ способов и методов, применяемых на различных этапах решения графических задач различных видов, позволяет оценить достоинства и недостатки каждого вида графических задач и сделать выводы о рациональности их применения для повышения качества графической подготовки.
Рецензенты:
Новоселов С.А., д.п.н., профессор, директор Института педагогики и психологии детства, Уральский государственный педагогический университет, г. Екатеринбург.
Куприна Н.Г., д.п.н., профессор, заведующая кафедрой эстетического воспитания, Уральский государственный педагогический университет, г. Екатеринбург.