Одна из наиболее важных функций банковского риск-менеджмента – управление активами и пассивами, или ALM (Asset-Liability Management). ALM – это скоординированное управление бухгалтерским балансом банка, учитывающее возможности альтернативных сценариев процентных ставок, ликвидности и погашений. Существует три метода управления активами и пассивами.
- Подбор соответствующих по срокам переоцениваемых балансовых активов и обязательств.
- Внебалансовое хеджирование балансовых рисков.
- Секьюритизация, позволяющая устранить риск бухгалтерского баланса.
К основным показателям оценки эффективности управления активами и пассивами относятся бухгалтерские показатели – чистый процентный доход (NII) или его относительная форма – чистая процентная маржа (NIM), а также экономическая мера – рыночная стоимость собственного капитала банка. Задача управления активами и пассивами – контроль и планирование реакции NIM банка и цены акции банка на непредвиденные изменения экономических условий.
Важнейшими составляющими ALM являются:
- измерение разрывов на базе интервалов сроков до погашения (0-90 дней, 91-180 дней и т.д.), позволяющих установить размер подлежащих переоценке активов и пассивов;
- прогнозирование величины процентных ставок, по которым будут переоцениваться эти фонды;
- проецирование будущих процентных доходов и процентных расходов;
- изучение возможных сценариев изменения экономических условий и уязвимости банка при реализации негативных сценариев.
Практическая реализация управления активами и пассивами возможна с помощью методов портфельной оптимизации. Данный инструментарий позволяет решить задачу формирования эффективного портфеля посредством определения таких пропорций распределения средств между допустимыми активами, которые обеспечивают минимальный риск портфеля при заданном уровне доходности. Динамическое программирование – один из наиболее мощных методов оптимизации. Возникновение этого метода связывают с именем американского ученого Р. Беллмана, который в начале 50-х годов ХХ века применил к ряду конкретных задач прием, названный впоследствии принципом оптимальности.
Описание динамической модели работы коммерческого банка
Планируется деятельность коммерческого банка на n лет (месяцев, кварталов, отчетных периодов и т.д.). На начало каждого года имеется некоторое количество денежных средств – это депозиты, собственный капитал и другие обязательства банка. Пусть ![]() (k = 1,…, n) – объем денежных средств в начале k-го года. Предположим, что объемы привлеченных банком денежных средств на начало каждого года {
(k = 1,…, n) – объем денежных средств в начале k-го года. Предположим, что объемы привлеченных банком денежных средств на начало каждого года {![]() } известны или имеется прогноз и возможные сценарии изменения данных показателей на n лет вперед.
} известны или имеется прогноз и возможные сценарии изменения данных показателей на n лет вперед.
Денежные средства {![]() } необходимо распределить между s видами активов, каждый из которых характеризуется некоторой доходностью. Обозначим через rik доходность i-го вида актива в k-м году. Предположим, что доходности всех s видов активов для всех периодов k (k = 1, …, n) известны или имеется прогноз и возможные сценарии изменения данных показателей на n лет вперед.
} необходимо распределить между s видами активов, каждый из которых характеризуется некоторой доходностью. Обозначим через rik доходность i-го вида актива в k-м году. Предположим, что доходности всех s видов активов для всех периодов k (k = 1, …, n) известны или имеется прогноз и возможные сценарии изменения данных показателей на n лет вперед.
Требуется определить такой способ распределения имеющихся денежных средств, чтобы чистый процентный доход банка за n лет был максимальным:
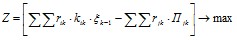 ,
,
где kik – доля денежных средств ![]() в i-м виде актива в k-м году;
в i-м виде актива в k-м году;
Пjk – объем j-го вида пассива в k-м году;
rjk – процентная ставка привлечения j-го вида пассива в k-м году.
Будем рассматривать процесс распределения имеющихся денежных средств как n – шаговый, в котором номер шага соответствует номеру года. Управление на k-м шаге состоит в выборе переменных k1k, k2k,...,ksk.
Уравнение состояния процесса можем записать в следующем виде:
![]() =
= ![]() ,
,
где ![]() - относительное изменение объема денежных средств в начале (k+1)-го года по сравнению с аналогичным периодом k-го года (зависит от экономических условий - прироста/оттока депозитов, изменения условий и объемов кредитования и т.д.);
- относительное изменение объема денежных средств в начале (k+1)-го года по сравнению с аналогичным периодом k-го года (зависит от экономических условий - прироста/оттока депозитов, изменения условий и объемов кредитования и т.д.);
![]()
![]() - прибыль, полученная в k-м году при оптимальном распределении средств между s видами активов, если в k-м году распределялось
- прибыль, полученная в k-м году при оптимальном распределении средств между s видами активов, если в k-м году распределялось ![]() денежных средств.
денежных средств.
Вычислительная процедура задачи динамического программирования начинается с введения функции ![]() , обозначающей прибыль, полученную за (n-k+1) лет, начиная с k-го года до конца рассматриваемого периода, при оптимальном распределении средств между s видами активов, если в k-м году распределялось
, обозначающей прибыль, полученную за (n-k+1) лет, начиная с k-го года до конца рассматриваемого периода, при оптимальном распределении средств между s видами активов, если в k-м году распределялось ![]() денежных средств.
денежных средств.
Функции ![]() для k = 1, 2, …, n удовлетворяют следующим функциональным уравнениям:
для k = 1, 2, …, n удовлетворяют следующим функциональным уравнениям:
![]()
При k = n
![]()
![]() определяется из уравнения состояния процесса.
определяется из уравнения состояния процесса.
Далее необходимо последовательно решать уравнения для всех возможных ![]() (k = 1, 2, …, n-1). Каждое из этих уравнений представляет собой задачу на оптимизацию функции, зависящей от s переменных.
(k = 1, 2, …, n-1). Каждое из этих уравнений представляет собой задачу на оптимизацию функции, зависящей от s переменных.
Ограничения модели
Для включения в нашу модель элементов управления рисками введем некоторые ограничения.
Ограничение несбалансированности по срокам финансовых активов и финансовых обязательств. Риск ликвидности обычно возникает в результате несбалансированности по срокам финансовых активов и финансовых обязательств кредитной организации (в том числе и вследствие несвоевременного исполнения финансовых обязательств одним или несколькими контрагентами кредитной организации) и/или возникновения непредвиденной необходимости немедленного и единовременного исполнения кредитной организацией своих финансовых обязательств. Как правило, при реализации этого риска кредитная организация для выполнения своих обязательств вынуждена привлекать на финансовом рынке дополнительные ресурсы и/или реализовывать имеющиеся активы, неся при этом незапланированные убытки в виде дополнительных затрат или недополученной прибыли.
Для оценки величины риска ликвидности, т.е. для оценки возможных затрат на поддержание платежеспособности кредитной организации удобно использовать инструментарий метода анализа разрывов ликвидности. Для проведения анализа разрывов обычно задается временной горизонт Т, который в зависимости от требуемой детализации анализа разбивается на необходимое количество диапазонов срочности N. Срочные активы и обязательства (включая внебалансовые составляющие) объединяются в единые совокупности активов и обязательств, которые соответствуют заданным диапазонам срочности:
![]() и
и ![]() ,
,
где ![]() (
(![]() ) - совокупная стоимость активов (обязательств), относящихся к i-му диапазону срочности;
) - совокупная стоимость активов (обязательств), относящихся к i-му диапазону срочности;
![]() (
(![]() ) - стоимость j-го актива (обязательства), срок до погашения (дюрация) которого (
) - стоимость j-го актива (обязательства), срок до погашения (дюрация) которого (![]() ) находится в границах i-го диапазона срочности;
) находится в границах i-го диапазона срочности;
![]() (
(![]() ) – нижняя (верхняя) граница i-го диапазона срочности.
) – нижняя (верхняя) граница i-го диапазона срочности.
Бессрочные ликвидные активы (денежные средства в кассе, остатки на счетах НОСТРО и т.п.) и текущие обязательства (вклады «до востребования», средства на расчетных счетах, остатки на счетах ЛОРО и т.п., в той части, которая может быть отозвана клиентами и контрагентами в текущий период) относят к диапазону срочности «до востребования». К диапазону срочности «до востребования» относят также срочные активы и обязательства в части их возможного досрочного погашения и исполнения.
Остальные бессрочные активы и обязательства (в том числе и обязательства «до востребования» в той части, которой кредитная организация может распоряжаться в текущий период), а также активы и обязательства со сроками погашения и исполнения (дюрациями), превышающими выбранный временной горизонт анализа, относят к диапазону срочности «без срока».
Величину ![]() еще называют кумулятивным разрывом (кумулятивным гэпом), которую для i-го диапазона срочности можно рассчитать с помощью следующей формулы:
еще называют кумулятивным разрывом (кумулятивным гэпом), которую для i-го диапазона срочности можно рассчитать с помощью следующей формулы:
![]()
Считается, что если банк имеет нулевой гэп, то его активы и пассивы согласованы по срокам. Таким образом, первое ограничение модели запишем так:![]() .
.
Нормативы ликвидности ЦБ РФ
В целях контроля за состоянием ликвидности банка инструкцией Центрального Банка N 110-И от 16 января 2004 г. «Об обязательных нормативах банков» устанавливаются нормативы мгновенной, текущей, долгосрочной ликвидности, которые регулируют (ограничивают) риски потери банком ликвидности и определяются как отношение между активами и пассивами с учетом сроков, сумм и типов активов и пассивов, других факторов.
Норматив мгновенной ликвидности банка (Н2) представляет собой отношение суммы высоколиквидных активов банка к сумме обязательств банка по счетам до востребования. Высоколиквидные активы – это денежные средства и средства на счетах до востребования. Обязательства по счетам до востребования – это вклады и депозиты до востребования и выпущенные кредитной организацией собственные векселя до востребования. Минимально допустимое числовое значение норматива Н2 устанавливается в размере 15 процентов.
Ограничения норматива представим в форме
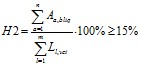 ,
,
где blig – признак высоколиквидного (highliqudity) актива;
vct – признак активов до востребования.
Аналогично представлены Нормативы текущей ликвидности Н3 и долгосрочной ликвидности (Н4).
Собственные и технологические ограничения
Для задач математического программирования характерно использование технологических ограничений в виде требований неотрицательности переменных.
Введем эти ограничения как
![]()
![]()
т.е. активы и пассивы не могут принимать отрицательные значения.
Во время плановых расчетов необходимо также соблюдать балансовое ограничение
![]()
показывающее, что сумма активов не может быть больше суммы пассивов, т.е. капитала и обязательств.
Помимо нормативных ограничений ЦБР на показатели работы банков, каждый банк в процессе управления операциями определяет собственные лимиты (ограничения) деятельности и составляющих портфелей активов и пассивов. Внешние ограничения в виде обязательных нормативов, устанавливаемых ЦБР, ни в коей мере не гарантируют устойчивого развития отдельно взятого банка. Банки вынуждены создавать целую систему внутренних лимитов. Структура лимитов банка отражает уровень риска, который руководство банка готово принять на себя при изменении конъюнктуры рынка и поведения контрагентов. Из соображений удобства компьютерной реализации представим собственные лимиты банка двусторонними неравенствами для каждого инструмента:
![]() ,
,![]()
При необходимости можно ввести и групповые ограничения. Результаты решения представлены на рис. 1.
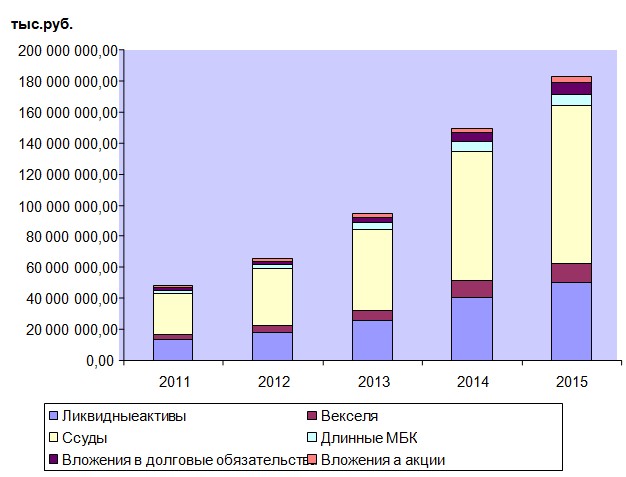
Рис. 1. Распределение денежных средств среди активов на 5-летний период при заданном сценарии развития экономической ситуации.
Подводя итоги всего сказанного, можно сделать следующие выводы касательно общей эффективности, актуальности и практического значения использования предлагаемой модели: оценка модели показывает, что динамическая задача планирования оптимальной системы портфелей банка может быть сформулирована как стандартная задача нелинейного программирования. Критерий линеен, ограничения экономических нормативов ЦБР нелинейны из-за операции деления показателей. Предполагается, что задачу можно решить с помощью стандартных программ нелинейной оптимизации.
Рецензенты:
Тихомирова Е.И., д.э.н., профессор, декан факультета математической экономики и информатики ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова» Министерства образования и науки РФ, г. Москва.
Зинчук Г.М., д.э.н., доцент, декан общеэкономического факультета ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова» Министерства образования и науки РФ, г. Москва.



