В последнее время одним из актуальных направлений развития компьютерных технологий в медицине становится обработка цифровых изображений: улучшение качества изображения, восстановление поврежденных изображений, распознавание отдельных элементов. Распознавание патологических процессов является одной из наиболее важных задач обработки и анализа медицинских изображений. При решении задач распознавания все чаще используются компьютерные системы диагностики – computer aided diagnostic (CAD) [8]. Алгоритм CAD – системы медицинских изображений, как правило, включает в себя сегментацию изображения, выделение объектов интереса («масс»), их анализ, параметрическое описание, их классификацию [6,13]. При этом выделенные объекты являются отражением патологического процесса в организме, а их классификация отвечает на вопрос, все ли выделенные объекты являются проявлением патологического процесса. В качестве методов параметрического описания выделенных объектов используется текстурный, гистограммный и морфометрический анализ [9,14], однако сочетание этих методов применяется редко. Классификация объектов интереса проводится по методу нейронных сетей, опорных векторов, дискриминантного анализа и пр. [6,8]. Вместе с тем задача автоматизированной диагностики патологических процессов по данным медицинских изображений далека от своего разрешения. Актуальной проблемой остается определение оптимальных методов параметрического описания объектов интереса, что может оказывать непосредственное влияние на качество их классификации [7,13].
Постановка задачи анализа медицинских изображений
Объекты интереса исследователя на медицинских изображениях, используемых в ранней диагностике, обычно бывают небольшими и малоконтрастными по сравнению с окружающим фоном. При визуальном обнаружении этих объектов – выполнении первого шага на пути диагностики по медицинскому изображению – могут возникнуть проблемы. С одной стороны, они обусловлены указанными особенностями самих изображений, с другой – ограниченностью характеристик зрительной системы исследователя и искажениями, возникающими в изображениях при их получении и отображении [1]. Исследование функций и особенностей работы современных специализированных систем для анализа и обработки медицинских изображений в различных целях показало, что эти системы обладают рядом недостатков. Основным недостатком представляется то, что большинство из систем содержит лишь широкий набор методов анализа и обработки изображений, доступный исследователю, без указаний, какой именно метод должен быть применен для достижения поставленной цели преобразования. В связи с этим выявлены следующие проблемы: невозможно гарантированно осуществить оптимальный (в смысле достижения поставленной цели преобразования) выбор метода (или комбинации методов) для обработки изображений, поскольку этот выбор основывается лишь на знаниях и опыте пользователя; осуществить перебор всех имеющихся в распоряжении исследователя методов (и их сочетаний) для достижения наилучшего результата обработки невозможно, поскольку это будет слишком затратным по времени. Поэтому для улучшения работы систем анализа и обработки медицинских изображений, очевидно, необходим метод, обеспечивающий автоматизированный выбор преобразования изображения [4,5]. При обработке и анализе изображений выделяют следующие основные этапы: фильтрация; предварительная обработка; сегментация; распознавание; диагностика. От результатов фильтрации и предварительной обработки напрямую зависит эффективность последующих этапов обработки изображений [12,14]. Этап фильтрации необходим для уменьшения разнообразных помех. Существуют различные типы фильтров: низкочастотные, высокочастотные, медианные, адаптивные и другие виды цифровых фильтров. В цифровой обработке изображений широко используется линейная фильтрация. Она базируется на использовании быстрых алгоритмов свертки. Статические маски фильтров не всегда гарантируют приемлемый результат, т.к. линейные фильтры приводят к сглаживанию перепадов яркости, а это в свою очередь усложняет задачу выделения границ. Нелинейная фильтрация имеет ряд преимуществ по сравнению с линейной: меньше искажает перепады яркости, что дает возможность точнее находить границы объектов и убирает импульсные помехи. Еще один вид фильтрации – это адаптивная фильтрация. Данный тип фильтрации обладает рядом преимуществ, таких как: локальная фильтрация, изменение локальной маски фильтра и размера апертуры фильтра [4,7]. Методы, используемые на этапе предварительной обработки, зависят от задач исследований, и они достаточно разнообразны. Они могут включать выделение наиболее информативных фрагментов, их увеличение, цветокартирование, изменение пространственного разрешения, изменение контрастного разрешения и т.п. [1,4,9]. Одни из основных действий, которые проводятся на этапе предварительной обработки, это изменение контрастности и яркости изображения. Методы изменения контрастности и яркости делятся на линейные, нелинейные и адаптивные. При применении соответствующих масок можно соединить два этапа (этап фильтрации и этап предварительной обработки) для обеспечения быстродействия. Этап предварительной обработки также предусматривает геометрические операции над изображением. К ним относится методы поворота изображения, увеличения и уменьшения изображения.
Сегментация медицинских изображений
Конечный результат анализа изображений во многом определяется качеством сегментации, а степень детализации выделяемых характеристик зависит от конкретной задачи [8,14]. Поэтому не существует отдельного метода или алгоритма, подходящего для решения всех типов задач сегментации – каждый из методов имеет свои достоинства и недостатки. Сегментация предназначена для выделения на изображениях областей с определёнными свойствами. Такие области обычно соответствуют объектам или их частям, которые определяют исследователи. Результатом сегментации является бинарное или иерархическое (мультифазное) изображение, в котором каждый уровень (фаза) изображения соответствует конкретному классу выделенных объектов. Сегментация является сложным моментом в обработке и анализе медицинских изображений биологической ткани, так как необходимо выделять области, соответствующие различным объектам или структурам на гистологических препаратах: клеткам, органоидам, артефактам и т.д. Это связано с высокой вариабельностью их характеристик, слабой контрастностью обрабатываемых изображений и сложной геометрической организацией объектов. По математическому аппарату, используемому для реализации методов сегментации, они делятся на три вида: пороговая сегментация; морфологическая сегментация; объединение (наращивание) областей [9].
Во многих случаях для получения более эффективного результата можно последовательно использовать разные методы сегментации. Например, для выделения границ используется операция морфологического градиента, после которой для фрагментов, соответствующих небольшим перепадам яркости, проводится пороговая сегментация. Для того чтобы выделить признаки исследуемого объекта, сопоставить их с данными из библиотеки и сделать вывод о вероятности наличия аномалии, необходимо предварительно выделить объект из множества, присутствующих на конкретном изображении. В большинстве случаев на исследуемом изображении присутствуют шумы, искажения, текстурные области, схожие с областями, принадлежащими исследуемому объекту. Все это затрудняет процесс выделения объектов и корректного отображения их границ, поэтому алгоритмы оконтуривания и сегментирования играют очень важную роль в процессе автоматизированной обработки. Оператор Cобеля – это один лучших алгоритмов выделения границ, он часто применяется как один из этапов более сложных и точных алгоритмов, как, например, оператор Канни. Оператор Собеля используется в области обработки изображений. Часто его применяют в алгоритмах выделения границ. Это дискретный дифференциальный оператор, вычисляющий приближенное значение градиента яркости изображения. Результатом применения оператора Собеля в каждой точке изображения является либо вектор градиента яркости в этой точке, либо его норма [2]. Другими словами, оператор вычисляет градиент яркости изображения в каждой точке. Так находится направление наибольшего увеличения яркости и величина её изменения в этом направлении. Результат показывает, насколько «резко» или «плавно» меняется яркость изображения в каждой точке, а значит, вероятность нахождения точки на грани, а также ориентацию границы. На практике вычисление величины изменения яркости (вероятности принадлежности к грани) надежнее и проще в интерпретации, чем расчет направления [5]. Математически градиент функции двух переменных для каждой точки изображения (которой и является функция яркости) – двумерный вектор, компонентами которого являются производные яркости изображения по горизонтали и вертикали. В каждой точке изображения градиентный вектор ориентирован в направлении наибольшего увеличения яркости, а его длина соответствует величине изменения яркости. Это означает, что результатом оператора Собеля в точке области постоянной яркости будет нулевой вектор, а в точке, лежащей на границе областей различной яркости, – вектор, пересекающий границу в направлении увеличения яркости [11]. Процесс сегментации с использованием оператора Собеля основан на простом перемещении маски фильтра от точки к точке изображения: в каждой точке (x,y) отклик фильтра вычисляется с использованием предварительно заданных связей. В случае линейной пространственной фильтрации отклик задается суммой произведения коэффициентов фильтра на соответствующие значения пикселей в области, покрытой маской фильтра. Как известно из курса математического анализа, направление вектора градиента совпадает с направлением максимальной скорости изменения функции f в точке (x,y). Важную роль при обнаружении контуров играет модуль этого вектора, который обозначается ∇ f и равен ![]() . Эта величина равна значению максимальной скорости изменения функции f в точке (x,y). Результатом применения оператора Собеля является двумерная карта градиента для каждой точки.
. Эта величина равна значению максимальной скорости изменения функции f в точке (x,y). Результатом применения оператора Собеля является двумерная карта градиента для каждой точки.
В решении задачи сегментации с использованием реальных снимков моделирование мало применимо, большее значение имеют практический опыт и экспертные суждения о результатах обработки изображений. Одним часто реализуемым программно методом является Canny. Практически это набор последовательно применяемых алгоритмов [7,10]. Такой подход устойчив к шуму и дает, как правило, лучшие результаты по сравнению с другими методами. Но так как это лишь набор алгоритмов, то и быстродействие данного метода уступает более простым операторам. Алгоритм Canny состоит из четырех этапов: размытие изображения (уменьшается дисперсия аддитивного шума на изображении); дифференцирование размытого изображения и вычисления значений градиента в направлении x и направлении y; не максимальное подавление; пороговая обработка [3]. В случае двух измерений эта формула задает поверхность, имеющую вид концентрических окружностей с распределением Гаусса от центральной точки. Пиксели, где распределение отлично от нуля, используются для построения матрицы свертки, которая применяется к исходному изображению. При этом значение каждого пикселя становится средневзвешенным для окрестности. Исходное значение пикселя принимает наибольший вес (имеет наивысшее Гауссово значение), и соседние пиксели принимают меньшие веса в зависимости от расстояния до них [10]. В теории распределение в каждой точке изображения будет ненулевым, что потребовало бы вычисление весовых коэффициентов для каждого пикселя изображения. Но на практике, когда рассчитывается дискретное приближение функции Гаусса, не учитывают пиксели на расстоянии свыше 3σ, т.к. они достаточно малы. Таким образом, программе, фильтрующей изображение, достаточно рассчитать матрицу [6σ]×[6σ], чтобы гарантировать достаточную точность приближения распределения Гаусса [5,9]. Далее происходит поиск градиента области при помощи свертки сглаженного изображения с производной от функции Гаусса как в вертикальном, так и в горизонтальном направлениях. Используем оператор Собеля для решения этой задачи. Процесс основан на простом перемещении маски фильтра от точки к точке изображения. В каждой точке (x,y) отклик фильтра вычисляется с использованием предварительно заданных связей. Для данного шага используем следующие матрицы:
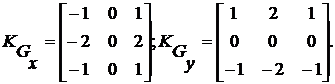
Gx и Gy – две матрицы, где каждая точка содержит приближенные производные по x и по y. Они вычисляются путем умножения матрицы Gx и Gy и суммированием обоих матриц, в результате полученный результат записывается в текущие координаты x и y в новое изображение.
В результате происходит первоначальное выделение краев на объекте интереса. Следующий шаг – применение порога для определения нахождения границы в данной точке изображения. Чем меньше порог, тем больше границ будет находиться, но тем более восприимчивым к шуму станет результат, выделяя лишние данные изображения. Наоборот, высокий порог может проигнорировать слабые края или получить границу фрагментами. Выделение границ использует два порога фильтрации: если значение пикселя выше верхней границы – он принимает максимальное значение (граница считается достоверной), если ниже – пиксель подавляется, точки со значением, попадающим в диапазон между порогов, принимают фиксированное среднее значение. В итоге задача сводится к выделению групп пикселей, получивших на предыдущем этапе промежуточное значение, и отнесению их к границе (если они соединены с одной из установленных границ) или их подавлению (в противном случае). Пиксель добавляется к группе, если он соприкасается с ней по одному из 8-ми направлений.
Достоинством алгоритма Canny является то, что при обработке изображения происходит адаптация к его особенностям. Это достигается путем ввода двухуровневого порога отсечения избыточной информации. Назначается два уровня порога, верхний – phigh и нижний – plow, где phigh>plow. Значения пикселей выше значения phigh идентифицируются как принадлежащие границе. При формировании текущей границы соседние пиксели со значениями величины градиента меньшими, чем рhigh, считаются принадлежащими границе до тех пор, пока они превышают рlow. В том случае, когда на всей границе нет ни одной точки со значением, большим верхнего порога, она удаляется. Такой подход позволяет получить довольно четкие границы объекта толщиной в один пиксель [11]. На рис. представлены результаты КАД – анализа изображения с применением оператора Собеля.
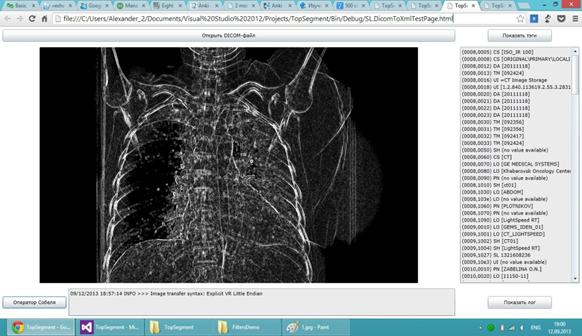
Медицинское изображение после применения оператора Собеля
Выводы
Результаты проведенных по гранту РФФИ №13 – 07 – 00667 исследований демонстрируют преимущество предложенного нами подхода к прогнозированию течения метастатического поражения скелета, регистрации динамических изменений данного органа, интеграционного анализа результатов комплексного исследования онкологических больных. Инновационный взгляд на рутинную обработку данных радионуклидных исследований может способствовать развитию нового направления медицинской информатики – ядерной биоинформатики. Ожидается встречный интерес к созданному программному комплексу со стороны разработчиков и производителей медицинского оборудования и практических врачей – радиологов, лучевых диагностов и других специалистов.
Рецензенты:
Кривошеев И.А., д.т.н., зав. лабораторией, Вычислительный центр ДВО РАН, г. Хабаровск.
Логинов И.П., д.м.н., профессор, зав. кафедрой, ГОУ ВПО «Дальневосточный государственный медицинский университет», г. Хабаровск.



