На сегодняшний день, Россия удерживает лидерство по количеству разводов. Если еще 10 лет назад распадался каждый третий брак, то сегодня уже каждый второй. Эти данные подтверждают не только отечественные, но и зарубежные исследователи. Так, по данным демографического ежегодника ООН 2012 года, Россия – первая среди стран с самым большим числом разводов.
Вопросами прочности браков занимается большое количество ученых разных специальностей: психологи, генетики, антропологи и другие. Среди причин, влияющих на прочность семейных отношений, обычно называют возраст, наследственный фактор, астрологические данные и др. Ряд американских ученых: Ник Стиннет, Джон Дефрайн, Уолтер Шумм и др. [10] считают, что прочность брака зависит от взаимности отношений, т.е. от уровня взаимного доверия супругов.
Целью настоящей работы является попытка применения современных методов искусственного интеллекта для построения методики прогнозирования уровня доверия супругов. Статья является продолжением серии публикаций, посвященных применению математического и программно-инструментального аппарата Пермской научной школы искусственного интеллекта в плохо формализуемых предметных областях [1-9].
Методика прогнозирования
В результате анализа публикаций по данной тематике, а также анализа анкетных опросов, для построения нейросетевой модели было выбрано семь входных параметров:
x1 - Глава семьи: 1 - мужчина, 2 - женщина.
x2 - Количество детей.
x3 - Наличие насилия в семье: 1 - есть, 0 - нет.
x4 - Уровень жизни: 1 - низший, 2 - средний, 3 - высший.
x5 - Наличие кредитов: 1 - есть, 0 - нет.
x6 - Средний возраст супругов на момент опроса.
x7 - Наличие собственного жилья: 1 - есть, 0 - нет.
Выходной параметр y кодировал значения: 0 – если супруги не доверяют друг другу, 1 – если супруги больше не доверяют, чем доверяют друг другу, 2 – если супруги больше доверяют, чем не доверяют друг другу, 3 – если супруги полностью доверяют друг другу.
Для обучения нейронной сети было сформировано множество примеров, основанных на результатах проведенного анкетирования, в котором участвовали супруги в возрасте от 18 до 65 лет. Множество примеров было разбито на обучающее, состоящее из 64 примеров, использованное для обучения сети, и тестирующее множество, состоящее из 17 примеров, предназначенное для проверки ее прогностических свойств.
C помощью технологии, сложившейся в Пермской научной школе искусственного интеллекта (www.PermAi.ru) [1, 3, 4], выполнялось проектирование нейронной сети, ее обучение и тестирование, а также эксперименты над нейросетевой математической моделью. Оптимальная структура нейронной сети представляет собой персептрон, имеющий семь входных нейронов, один скрытый слой с тремя нейронами и один выходной нейрон. В качестве активационных функций нейронов скрытого слоя и выходного нейрона использовались сигмоидные функции.
После оптимизации и обучения нейронной сети ее прогностические свойства проверялись на примерах тестирующего множества примеров, которые в процессе обучения нейросети не участвовали. Среднеквадратичная погрешность тестирования нейронной сети, в том числе определенная по методике многократной перекрестной проверки, не превысила 5 %. Таким образом, можно утверждать, что нейронная сеть усвоила закономерности моделируемой предметной области и адекватна ей.
Результаты вычислительных экспериментов и их обсуждение
После того, как работа нейросети проверена на тестовых примерах, и таким образом проверена адекватность нейросетевой математической модели, можно приступать к ее исследованию. Прежде всего, по методике [1, 4] путем поочередного исключения входных нейронов и наблюдением за погрешностью сети была определена значимость входных параметров модели, т.е. – степень их влияния на результат моделирования. Как видно из гистограммы рис. 1, наиболее значимыми параметрами оказались: насилие в семье и количество детей, а наименее значимым – уровень жизни.
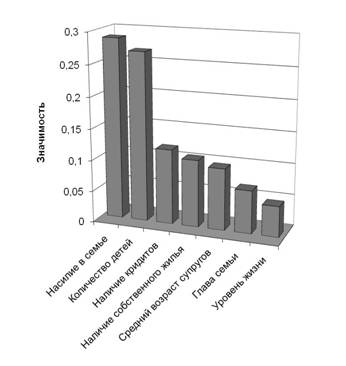
Рис. 1. Гистограмма распределения значимости входных параметров модели
Как известно [1, 3, 4], применение методов нейросетевого моделирования позволяет не только предсказывать будущие события, но и получать рекомендации, позволяющие активно влиять на эти события. Такие рекомендации можно получать путем проведения виртуальных компьютерных экспериментов. Для исследования закономерностей моделируемой предметной области были выбраны параметры пяти супружеских пар (см. таблицу 1) с разными уровнями доверия супругов.
Таблица 1
Характеристики исследуемых супружеских пар
|
Номер пары |
Глава семьи |
Количество детей |
Наличие насилия |
Уровень жизни |
Наличие кредитов |
Средний возраст |
Наличие собственного жилья |
Уровень доверия |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
y |
|
|
1 |
2 |
0 |
1 |
2 |
0 |
32 |
1 |
0 |
|
2 |
1 |
0 |
1 |
3 |
0 |
42 |
1 |
1 |
|
3 |
1 |
1 |
0 |
2 |
1 |
33 |
1 |
2 |
|
4 |
2 |
2 |
0 |
2 |
1 |
23 |
1 |
2 |
|
5 |
1 |
1 |
0 |
2 |
0 |
22 |
1 |
3 |
Изменяя входной параметр x3, кодирующий «Наличие насилия в семье», и производя вычисления с помощью обученной нейронной сети, можно проследить, как будет меняться уровень доверия супругов в зависимости от этого параметра. Анализируя полученную таким образом гистограмму, изображенную на рис. 2, можно заключить, что наличие насилия во всех пяти рассматриваемых семьях существенно понижает уровень доверия супругов.
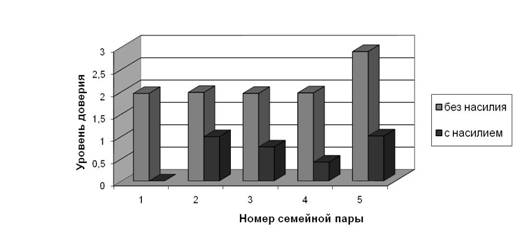
Рис. 2. Зависимость уровня доверия супругов от наличия насилия в семье
На рис. 3 представлены результаты прогнозирования уровня доверия супругов при изменении параметра x2, кодирующего количество детей в семье. Вычисления с помощью нейронной сети показали довольно значительную прямую зависимость: чем больше детей в семье, тем выше уровень доверия супругов.
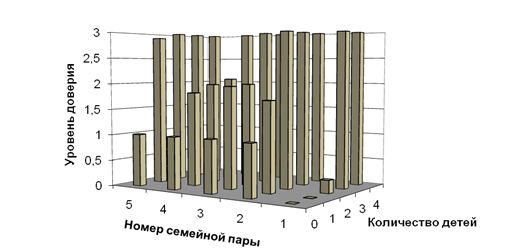
Рис. 3. Зависимость уровня доверия супругов от количества детей в семье
На рис. 4 представлены зависимости влияния экономической составляющей на уровень доверия супругов. Как видно из рисунка, уровень жизни семьи для разных супружеских пар влияет на уровень доверия супругов по-разному: он может приводить как к повышению, так и к уменьшению уровня доверия супругов. Все зависит от сочетания остальных параметров семьи – возраста, количества детей, наличия насилия и др.
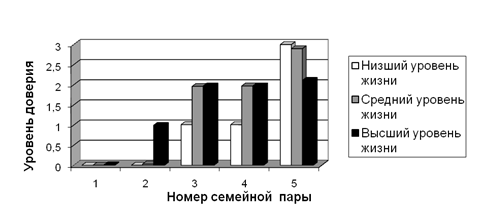
Рис. 4. Зависимости уровня доверия супругов от уровня их материального благополучия
Заключение
Разработана нейросетевая математическая модель, реализованная в виде компьютерной программы, позволяющей выполнять прогнозирование уровня доверия супругов. Выявлены и исследованы наиболее значимые параметры, оказывающие наибольшее влияние на уровень доверия супругов. Показана принципиальная возможность применения нейросетевых технологий в семейной сфере. Компьютерная программа может быть использована для получения прогнозов и разработки полезных рекомендаций, направленных на увеличение прочности семейных пар. Воспользоваться компьютерной программой можно с сайта Пермской научной школы искусственного интеллекта www.PermAi.ru.
Автор выражает благодарность своим научным руководителям – профессору Л.Н. Ясницкому и доценту Ф.М. Черепанову за предоставленные методики, программный инструментарий и консультации.
Рецензенты:
Русаков С.В., д.ф.-м.н., профессор, заведующий кафедрой прикладной математики и информатики, Пермский государственный национальный исследовательский университет, г. Пермь.
Пенский О.Г., д.т.н., доцент, профессор кафедры процессов управления и информационной безопасности, Пермский государственный национальный исследовательский университет, г. Пермь.



