Теорию ограничений систем (ТОС, с англ. Theory of Constraints) сформулировал и обосновал израильский ученый Элияху Моше Голдратт в 80-е годы прошлого века. Он ее активно развивал и внедрял в области производства, управления проектами и даже образовательных процессов. Теория произвела революцию в бизнес-среде и получила большое количество последователей, взявшихся за ее дальнейшее совершенствование. Среди наиболее известных – Лоуренс Лич и Уильям Детмер.
Целью данного исследования является установление особенностей применения ТОС и следующего из нее метода критической цепи к календарному планированию строительных проектов.
В основе данной работы лежат труды Э. Голдратта, Л. Лича, У. Детмера по теории ограничений и ее использованию в управлении проектами. Исследование проводилось с применением системного анализа и сравнения явлений и результатов.
Основные предпосылки к формированию ТОС впервые обозначены в книге Э. Голдратта «Цель: процесс постоянного совершенствования», увидевшей свет в 1984 г. Для области управления проектами строительства и построения календарных планов интересны следующие утверждения:
-
«Система локальных оптимумов совсем не оптимальная система» [2]. Здесь Э.Голдратт делает акцент на ошибочность традиционного подхода к пониманию производительности системы, при котором считается, что максимизация производительности каждой составной части (звена) приводит к максимизации результатов работы всей системы в целом;
-
«Узкие звенья диктуют уровень связанного капитала, так же как и производительность системы» [2]. Производительность системы определяется производительностью «узкого звена» («бутылочного горлышка»), которое и выступает в роли ограничения. Поэтому для увеличения эффективности работы достаточно повысить производительность одного звена, что автоматически за счет ускорения прохода через цепь событий уменьшит уровень связанного капитала, а также операционных расходов.
В этой же книге («Цель: процесс постоянного совершенствования») Э. Голдратт формулирует последовательность шагов оптимизации и балансировки работы системы:
Шаг 1. Найти ограничения системы;
Шаг 2. Решить, как эффективно использовать ограничения системы;
Шаг 3. Согласовать все остальные действия с этим решением;
Шаг 4. Повысить пропускную способность ограничения;
Шаг 5. Если на предыдущем этапе узкое звено было устранено, то вернуться к шагу 1 [2, 3].
Теория ограничений относится к категории методов, построенных на логических процедурах, среди которых JIT («точно вовремя») и TQM (тотальное управление качеством) [1]. Эти управленческие философии во многом дополняют друг друга. Хотя в чистом виде они мало применимы к управлению проектами. Но конвергенция отдельных элементов данных теорий позволяет сделать огромный шаг в совершенствовании данного процесса.
Основная причина, приводящая к срыву сроков сдачи проектов, превышению бюджета и урезанию содержания, а, следовательно, и снижению дохода от их реализации – это неопределённость факторов и условий, в которых будет осуществляться проект [1]. Иначе Э. Голдратт называет эту причину «Мерфи», т.е. законы Мерфи: «Whatevercangowrong, will» [6] (все, что может пойти неправильно, обязательно пойдет неправильно).
На практике люди всегда стремятся учесть эту неопределенность путем заложения подстраховки при оценке длительности операций, которая, по наблюдениям Э. Голдратта, может достигать 200 % [1]. Тем не менее успешно, т.е. в срок и с соблюдением плановых показателей рентабельности, заканчивается только 1/3 проектов [4].
Усиление действия законов Мерфи вплоть до невозможности устранения их последствий происходит из-за:
1. Потери сфокусированности исполнителей из-за одновременного выполнения и контроля нескольких задач [1]. Многозадачность ведет к увеличению длительности работы по причине «перепрыгивания» от одного процесса к другому. Л. Лич приводит пример, когда исполнитель в течение дня последовательно работает над тремя задачами, продолжительность каждой из которых при условии непрерывности составляет одну неделю. При ежедневном одновременном выполнении трех процессов их длительность увеличивается до трех недель [4], что провоцирует запаздывание и последующих связанных задач (рис.1). Кроме того, необходимо добавить время на возвращение к процессу после его остановки, т.е. на восстановление подробностей, особенно если задачу сопровождает сложная мыслительная работа;

Рис.1. Влияние многозадачности на длительность отдельной операции в составе проекта
2. Дефекта применяемого контрольного механизма, измеряющего прогресс проекта [1]. Традиционный отчет о ходе реализации проекта, как правило, отражает следующую закономерность: первые 90 % работы отнимают 10 % времени, а последние 10 % – оставшиеся 90 % времени. При данной ситуации своевременное обнаружение мест проекта, где проявился закон Мерфи и где требуется проведение корректирующих мероприятий, невозможно;
3. Студенческого синдрома: «спешить некуда, поэтому начинаем в последнюю минуту» [1]. Когда человек считает, что на выполнение задачи достаточно времени, исчезает мотивация к немедленному началу процесса. Резерв исчерпывается до того, как начинается работа, и проявление закона Мерфи в дальнейшем компенсировать не удается, а это приводит к запаздыванию проекта;
4. Действия закона Паркинсона: «работа расширяется, чтобы заполнить все время, остающееся до ее завершения» [5]. Э. Голдратт замечает: «При последовательных элементах отклонения по времени не усредняются. Опоздания аккумулируются, в то время как выигрыши по времени не аккумулируются» [1]. Исполнитель, завершивший задачу ранее обозначенного срока, никогда об этом не заявляет, а предпринимает действия по улучшению выполненной работы и сдаче результатов согласно плану. По-другому проявляют себя запаздывания, которые накапливаются от звена к звену. Следствие: дата завершения проекта отодвигается на сумму этих запаздываний.
Данные факторы приводят к полному расходованию заложенной подстраховки, какой бы большой она ни была, задолго до даты завершения проекта.
Для снижения влияния перечисленных воздействий Э. Голдратт предложил в управлении проектами использовать метод критической цепи (CriticalChainProjectManagement – CCPM). Общий алгоритм соответствует ранее обозначенным 5 шагам ТОС.
Ограничением проекта, его узким звеном, является критический путь, т.е. самая длинная последовательность зависимых элементов проекта, которые не имеют резерва времени.
В основе критического пути лежат ограничения по времени, предопределенные исключительно технологическими связями задач. При этом никак не учитывается зависимость элементов с точки зрения их исполнителя. В случае если ресурс занят на одном некритическом пути, а параллельно его работа требуется и на другом некритическом пути, провоцируется опоздание, которое приводит к изменению критического пути. Т.е. даже если элементы в составе проекта не связаны технологически, они могут оказаться зависимы от одного ресурса. Связи элементов с точки зрения и технологии, и исполняющего ресурса учитываются в критической цепи. Э. Голдратт определяет ее как самую длинную цепь, состоящую из отрезков, зависящих от пути, и отрезков, зависящих от ресурса [1].
Основное отличие метода критического пути от метода критической цепи состоит в том, что в критическом пути неопределенность учтена внутри каждой задачи, а в критической цепи вынесена отдельно в конец проекта (рис.2). При этом необходимо отметить, что если в проекте нет ограничения по ресурсам (исполнителям), то критический путь и критическая цепь совпадают.
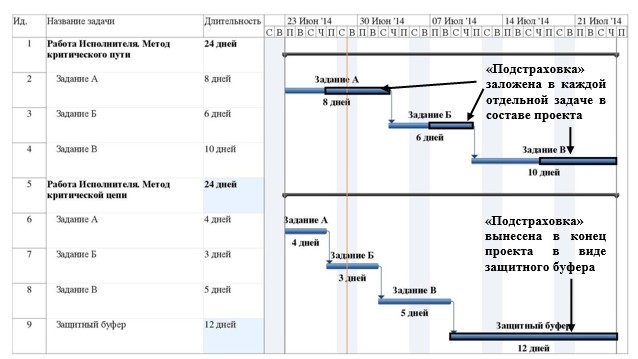
Рис.2. Графическое сравнение методов критического пути и критической цепи
Сравнение методов критического пути и критической цепи по ряду показателей приведено в табл.1.
Таблица 1
Сравнение методов критического пути и критической цепи
|
№ п/п |
Наименование показателя сравнения |
Метод критического пути |
Метод критической цепи |
|
1 |
Определение |
Критический путь - самая длинная последовательность зависимых элементов проекта, которые не имеют резерва времени |
Критическая цепь - самая длинная последовательность зависимых элементов проекта, состоящая из отрезков, не имеющих резерва времени с учетом ограничений по использованию ресурсов |
|
2 |
Статичность ограничения |
Критический путь может меняться в течение реализации проекта в зависимости от фактических дат завершения той или иной задачи |
Критическая цепь не меняется в течение реализации проекта |
|
3 |
Фиксируемые даты |
Критический путь определяет даты начала и окончания проекта |
Критическая цепь фиксирует только дату завершения проекта (после добавления проектного буфера). Начало проекта может определяться и некритической задачей |
|
4 |
Определение продолжительности задач |
Продолжительность задач оценивается расчетным или экспертным методом с учетом «подстраховки» на основании предыдущего негативного опыта |
Продолжительность задач, определенная расчетным или экспертным методом с учетом "подстраховки" на основании предыдущего негативного опыта, сокращается на 50 % |
|
5 |
Учет неопределенности |
Неопределенность учитывается косвенным образом при определении продолжительности каждой отдельной задачи |
Неопределенность учитывается в явном виде в питающих буферах и проектном буфере |
|
6 |
Управление календарным планом |
Чтобы проект реализовывался в соответствии с графиком, каждая отдельная задача должна выполняться в установленные сроки |
Чтобы проект реализовывался в соответствии с графиком необходимо контролировать защитные буферы проекта, которые поглощают коэффициент неопределенности каждой отдельной задачи |
|
7 |
Контроль календарного плана |
Отслеживаются даты начала и окончания каждой задачи. На дату завершения проекта влияет каждое опоздание, поэтому их необходимо внимательно отслеживать |
Даты начала и окончания отдельных задач непринципиальны. Необходимо внимательно отслеживать состояние защитных буферов и активность их расходования |
|
8 |
Оценка прогресса проекта |
Для оценки прогресса проекта на определенную дату используется фиксированная дата завершения той или иной стадии проекта (веха) |
Все даты завершения той или иной стадии проекта (вехи) являются плавающими. Для оценки прогресса достаточно определить находится ли этап в стадии завершения, а также проанализировать расход защитного буфера для обозначения вероятности завершения этапа к определенной дате |
|
9 |
Резервы времени на некритических путях |
Резервы времени, которые имеются на некритических путях, не важны и не отслеживаются |
Для защиты критической цепи некритические пути должны иметь питающие буферы, статус которых постоянно отслеживается |
|
10 |
Отношение к многозадачности |
Прогресс каждого реализуемого проекта (задачи) важен, поэтому режим многозадачности при использовании ресурсов сохраняется |
Многозадачность в работе ресурсов ограничивается вплоть до задержки начала реализации других параллельных проектов (задач) |
Надежность даты завершения проекта в CCPM обеспечивается добавлением в график буферов, защищающих критическую цепь от воздействия законов Мерфи.
В CCPM предполагает два вида буферов:
-
Буфер на слияние путей, который добавляется в месте впадения некритической цепи в критическую. Это обеспечивает своевременное начало работ на этапе в составе критической цепи в случае возникновения сбоя на некритическом элементе;
-
Проектный буфер, размещаемый в конце проекта. Он позволяет компенсировать опоздания, проявившиеся на критической цепи.
Вариантов критической цепи в составе одного проекта может быть несколько в зависимости от принятого решения по устранению конкуренции за ресурсы. А это, в свою очередь, оптимизационная задача. Но Э. Голдратт не придает большого значения форме распределения ресурсов из-за отсутствия «действительной разницы», превышающей степень неопределенности в проекте [1], которая гасится в закладываемых буферах.
Сравнение нескольких вариантов простого календарного плана строительства двух коттеджей с укрупненной разбивкой работ на 6 этапов показало, что метод критический цепи позволяет сформировать график, который будет на 16 % эффективнее метода критического пути (см. рис.3, 4).
Разброс значений при сопоставлении трех графиков по методу критической цепи в зависимости от варианта устранения конфликта ресурсов не превышает 4 %, что подтверждает мнение Э. Голдратта о неэффективности оптимизации и позволяет при планировании использовать любую форму выравнивания ресурсов.
Результаты сравнения отображены в табл. 2.
Таблица 2
Сравнение графиков, сформированных по методу критического пути и критической цепи
|
Наименование |
Кол-во дней |
|
Метод критического пути |
|
|
До выравнивания ресурсов |
75 |
|
После выравнивания (по двум вариантам - с помощью встроенной функции MS Project) |
92 |
|
Метод критической цепи |
|
|
Выравнивание с помощью встроенной функции MS Project (вариант 1) |
77 |
|
Выравнивание вручную (вариант 2) |
74 |
|
Выравнивание вручную (вариант 3) |
75 |
|
Сопоставление графиков по методу критической цепи |
|
|
Сравнение - вариант 1 / вариант 2 |
4% |
|
Сравнение - вариант 2 / вариант 3 |
1% |
|
Сравнение - вариант 3 / вариант 1 |
3% |
|
Сравнение метода критического пути и метода критической цепи (по максимальным значениям) |
16% |
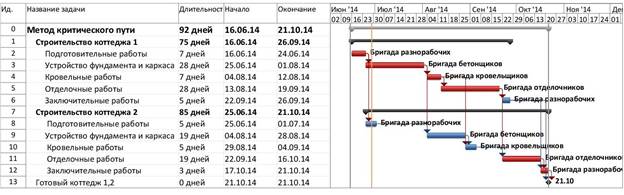
Рис. 3. График проекта по методу критического пути
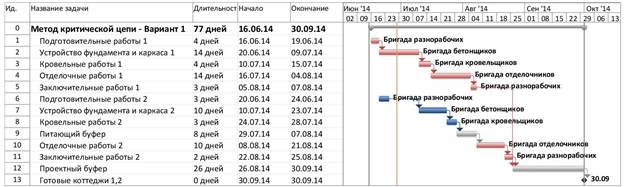
Рис. 4. График проекта по методу критической цепи – вариант 1
По результатам проведенного исследования можно сделать следующие выводы:
-
Производительность любой системы, в т.ч. и строительно-инвестиционного проекта, определяется производительностью самого слабого звена, которое выступает в роли ограничения; в строительном проекте таким ограничением является критический путь;
-
Из-за наличия ограничения, а также неопределенности, присущей функционированию системы, в подавляющем большинстве проектов имеют место срывы сроков, превышение бюджета и урезание содержания;
-
Метод критического пути учитывает ограничение проекта по времени, но не принимает во внимание ограничения по ресурсам (исполнителям), поэтому в строительных проектах более обоснованно применение метода критической цепи (зафиксировано улучшение календарного плана на 16%);
-
Эффективность оптимизационных алгоритмов и методов сомнительна, их применение является трудоемким процессом, который не дает существенного улучшения результатов календарного планирования (простой пример выявил различия между вариантами графика, не превышающими 4 %).
Рецензенты:
Болотин С.А., д.т.н., профессор, ФГБОУ ВПО «СПбГАСУ», г. Санкт-Петербург.
Ватин Н.И., д.т.н., профессор, ФГОУ ВПО «СПбГПУ», г. Санкт-Петербург.



