В настоящее время хаотические сигналы применяются в различных областях науки и технологий — в металлургии [2], машиностроении [17], задачах автоматизации технологических процессов [6; 8; 20], финансовой сфере [1; 20], геологии [18], медицине [14], для моделирования трафика в компьютерных сетях [4, 16], для обеспечения безопасности в корпоративных сетях [9] и облачных инфраструктурах [23], в сельском хозяйстве [24] и многих других. Это говорит о большом междисциплинарном значении научных результатов в области теории хаотической динамики. Во многих практических приложениях исследователям представляется удобным действовать в предположении о хаотическом характере наблюдаемого процесса. Аттрактор просто восстановить, существует множество численных методов оценки размерности. Разработаны методы приближенного решения обратной задачи динамики, т.е. восстановления заданного вида дифференциальных уравнений по экспериментальным данным [2; 3; 7; 11; 12; 19].
Однако предположение о хаотичности динамики часто строится только на оценках необходимых условий существования хаоса, таких как оценка старшего показателя Ляпунова. В статье изложен алгоритм выявления слабого нарушения симметрий для анализа хаотичности восстановленного фазового портрета [15; 25]. Показано, как результаты вычислений могут быть использованы для идентификации систем.
1. Постановка задачи
Для исследования используется временной ряд ![]() , при этом предполагается, что временной ряд порожден системой, дискретизированная форма который имеет вид:
, при этом предполагается, что временной ряд порожден системой, дискретизированная форма который имеет вид:
![]() , (1)
, (1)
где![]() — n–мерная точка в пространстве состояний; y — наблюдаемый одномерный процесс; k — дискретное время (номер); f, g — вектор функции.
— n–мерная точка в пространстве состояний; y — наблюдаемый одномерный процесс; k — дискретное время (номер); f, g — вектор функции.
Использование дискретных моделей позволяет оперировать с данными, полученными в результате эксперимента, и не накапливать ошибки, связанные с переходом к непрерывным моделям, однако это усложняет качественный анализ процессов.
Фазовая траектория, как известно, это траектория, изображающая, как изменяется со временем t состояние динамической системы x. Для дискретных систем, состояния соединяются линиями, в соответствии с последовательностью отсчетов k = 1, 2, …. Область, к которой эволюционируют (сходятся) все возможные траектории движения систем, называется аттрактором. Для дискретных систем, так же как и для непрерывных, аттрактор представляет собой точку, для колебательных систем — замкнутые траектории (циклы). Для хаотических систем существует аттрактор, который называется странным, в этом случае траектории стягиваются, но не в точку, кривую, тор, а в некоторое подмножество фазового пространства.
В настоящее время существуют различные точки зрения на число и характер сценариев перехода к хаосу:
-
сценарий Фейгенбаума (через каскад бифуркаций удвоения периода);
-
сценарий Афраймовича-Шильникова (модель Рюэля-Такенса) (через разрушение двумерного тора или через разрушение замкнутой инвариантной кривой);
-
сценарий Помо-Манневиля (чередование во времени почти регулярных колебаний с интервалами хаотического поведения).
Исследование сценариев перехода к хаосу играет важную роль на практике, так как в ряде случаев позволяет предсказать возможность наступления хаотического режима поведения динамической системы при изменении управляющих параметров. При разработке метода использовался второй тип сценария, который позволяет использовать методы качественной нелинейной динамики.
Аттрактор является инвариантной характеристикой системы, т.е. сохраняется при действиях преобразований. Динамические системы, для которых n-мерный фазовый объем уменьшается, называются диссипативными, если фазовый объем сохраняется, то такие системы носят название консервативных. У консервативных систем всегда существует хотя бы один закон сохранения. Законы сохранения определяются симметриями, допускаемыми системой.
Задача, рассматриваемая в статье, состоит в построении модели вида (1) по наблюдаемому временному ряду.
2. Моделирование систем с хаотической динамикой на основе оценки слабого нарушения симметрий в реконструированном аттракторе
Разработан метод моделирования систем с хаотической динамикой [7; 19; 21], позволяющий находить решение обратной задачи динамики на минимальном инвариантом многообразии в классе аффинных систем.
Суть метода состоит в следующем. Исходными данным является временной ряд, порожденный (предположительно) системой с хаотической динамикой.
-
Вычисляются численными методами необходимые условия существования хаоса — старший показатель Ляпунова (для хаотической динамики должен быть больше нуля) и др. [4; 7].
-
Восстанавливается аттрактор по методу Паккадра (метод задержки) [7].
-
Если подтверждается предположение о хаотической динамике, то исследования продолжаются.
-
На основе анализа реконструированного аттрактора проверяется наличие симметрий (в условиях слабого нарушения симметрий) [21].
-
. По принятым симметриям по формуле Хаусдорфа-Ли строится вид уравнений в минимальном инвариантом многообразии [19].
-
Структура уравнений параметрически идентифицируется [8].
-
Оценивается качественное расхождение динамики модели и исходного ряда.
На выходе – модель в форме конечноразностных уравнений.
Первым двум этапам метода посвящено значительное количество работ, поэтому их обсуждение выходит за рамки настоящей статьи. Остановимся подробно на четвертом этапе.
Алгоритм поиска симметричных участков реконструированных траекторий в условиях слабого нарушения симметрий был разработан О.В. Козловым [5]. Надо отметить, что в данной постановке задача поиска почти симметричных фрагментов является NP-полной. Алгоритм состоит из пяти этапов. Исходными данными алгоритма служат n-мерные точки, принадлежащие реконструированному аттрактору в фазовом пространстве.
1 этап. Выделение монотонных фрагментов с единственным локальным экстремумом. В n-мерном фазовом пространстве выделяется фрагмент ![]() , состоящий из m действительных точек, представляется в виде матрицы
, состоящий из m действительных точек, представляется в виде матрицы ![]() :
:
![]() ,
,
т.е. в виде матрицы ![]() .
.
2 этап. Преобразование фрагмента в дескриптор — образ, инвариантный относительно переноса, поворота и масштабирования исходного фрагмента, а также получение численных показателей этого преобразования. Результатом процедуры нормализации является дескриптор фрагмента ![]() , матрица, осуществляющая преобразование фрагмента в его дескриптор, а также набор показателей и матриц всех промежуточных преобразований:
, матрица, осуществляющая преобразование фрагмента в его дескриптор, а также набор показателей и матриц всех промежуточных преобразований: ![]() матриц. Данная процедура изложена в [21].
матриц. Данная процедура изложена в [21].
3 этап. Оценка нарушения симметрии. После получения дескрипторов двух предположительно симметричных фрагментов ![]() и
и ![]() можно дать численную оценку расхождения (расстояния) между ними
можно дать численную оценку расхождения (расстояния) между ними ![]() , на основе разложения в ряд Фурье.
, на основе разложения в ряд Фурье.
Для вычисления расстояния между фрагментами предлагается суммировать расхождения соответствующих элементов спектров этих контуров после дискретного преобразования Фурье, причем более высокочастотные (пары, близкие к центру спектра) элементы спектра имеют меньшее влияние на показатель близости, чем низкочастотные.
Соответствующий критерий имеет вид:
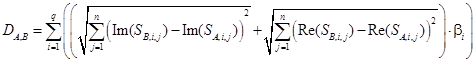 , (2)
, (2)
где q — количество сопряженных пар элементов спектра, n — размерность фазового пространства, ![]() — коэффициенты дисконтирования (
— коэффициенты дисконтирования (![]() ), определяющие степень важности составляющих спектра по частотам,
), определяющие степень важности составляющих спектра по частотам, ![]() — соответствующие элементы спектра контуров A и B. В практических приложениях использовался экспоненциальный вид зависимости
— соответствующие элементы спектра контуров A и B. В практических приложениях использовался экспоненциальный вид зависимости ![]() от номера члена ряда разложения Фурье.
от номера члена ряда разложения Фурье.
Для оценки схожести дескрипторов вводится показатель
![]() , (3)
, (3)
где ![]() — оценка, вычисляемая по формуле (2).
— оценка, вычисляемая по формуле (2).
Предложены критерии оценки решения. Средний показатель схожести пар дескрипторов фрагментов, входящих в решение:
![]() , (4)
, (4)
где k — количество фрагментов в решении n, а Ni,j — схожесть фрагментов i и j, вычисляемая в соответствии с (3). Длина покрытия фрагментами исходного контура:
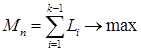 , (5)
, (5)
где k — количество фрагментов в решении n, а Li – длина фрагмента i.
Задача поиска решения многокритериальна. Происходит однокритериальный поиск последовательными этапами, на каждом из которых длина покрытия фрагментами решений исходного контура ограничена снизу, а в качестве оценки используется критерий (4). Этап завершается при выполнении условий сходимости, количество этапов задается изначально.
Обобщенный критерий оценки для выбора единственного решения:
![]() ,
,
где n — номер особи; L – длина исходного контура; ![]() вычисляется по (5).
вычисляется по (5).
4 этап. Итеративная процедура генетического отбора решений. Для решения использовался генетический отбор [21].
Весь алгоритм реализован в форме программы в среде MATLAB.
Заметим, что по сути происходит проверка, допускает ли система заданные преобразования, в условиях слабого нарушения симметрии. Последнее проверяется как существование некоторой малой величины, незначительно отклоняющейся от симметричного отображения. (Например, слабое нарушение симметрии видно, как почти похожие петли в аттракторе.)
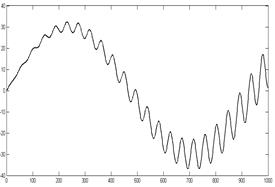
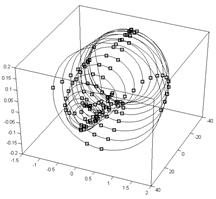
Приведем тестовый пример для иллюстрации работы алгоритма и оценки его работоспособности. В качестве исходных данных будем использовать временной ряд, приведенный на рис. 1а. Исходный набор данных состоит из 1000 точек. Реконструированный портрет приведен на рис. 1б. Контур был подвергнут расстановке маркеров (рис. 2а). Общее количество маркеров: 126. После маркировки из 7860 возможных контуров было отобрано 2807, остальные не удовлетворили ограничениям по длине: от 2 до 200 точек исходного контура. Каждый фрагмент интерполирован 60 равномерно расположенными по его длине точками и подвергнут процедуре нормализации. После этого была построена матрица смежности фрагментов (рис. 2б).
 а)
а) 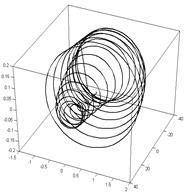 б)
б)
Рис. 1. Исходные временной ряд (а) и реконструированный фазовый портрет (б)
 а)
а) 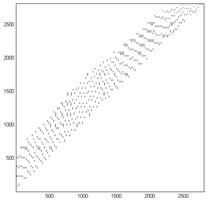 б)
б)
Рис. 2. Размеченный фазовый портрет (а) и матрица смежности фрагментов (б)
Осуществлен эволюционный подбор решения (размер популяции 200, показатели вероятности мутации ![]() и
и ![]() ; количество шагов ограничения длины: 8, элитарный отбор в новое поколение, тип выбора родителей — аутбридинг, особи в популяции уникальны), и отобрано решение-победитель. Популяция сошлась 8 раз за 817 итераций, решение-победитель: схожесть фрагментов 0.6271, длина 682.
; количество шагов ограничения длины: 8, элитарный отбор в новое поколение, тип выбора родителей — аутбридинг, особи в популяции уникальны), и отобрано решение-победитель. Популяция сошлась 8 раз за 817 итераций, решение-победитель: схожесть фрагментов 0.6271, длина 682.
Симметричные фрагменты фазовой траектории в условиях слабого нарушения (почти симметричные фрагменты) показаны на рис. 3а сплошной линией, соответствующие им фрагменты временного ряда на рис. 3б.
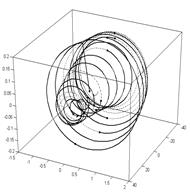
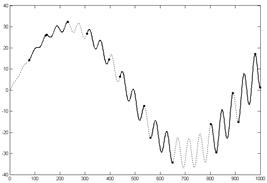
Рис. 3. Почти симметричные участки фазовой траектории (а), исходных данных (б)
4. Моделирование и генерация хаотического сигнала
В [13] показано, что робастный хаос может возникнуть в кусочно-гладких системах. Этот результат облегчает задачу моделирования систем с хаотической динамикой. Попытки провести параметрическую идентификацию модели с произвольно выбранными видами нелинейностей, как правило, вообще не находят решения. Если решение найдено (что, скорее, случайность, чем закономерное явление), то решения будут естественно чувствительны к незначительным изменениям параметров. Действительно, во многих физических явлениях хаос возникает при незначительном изменении параметра, однако в технических приложениях использование хаотического режима, как правило, требует поиска менее чувствительных, т.е. робастных моделей. Этого требует сама суть экспериментов с техническими системами, а также ошибки вычислений и измерений. Кроме того, для задач синтеза управлений эффективно использовать хаотические свойства систем, но при условии, что хаотический режим не изменяет качественного поведения в некотором диапазоне параметров.
Предложено использовать модель в виде
![]()
Здесь нелинейная функция ![]() определяется из найденных симметрических свойств фазовой траектории по формуле Хаусдорфа-Ли [см. доказательство в 19]; uk — дискретизированная кусочно-непрерывная функция времени (например, кусочно-линейная).
определяется из найденных симметрических свойств фазовой траектории по формуле Хаусдорфа-Ли [см. доказательство в 19]; uk — дискретизированная кусочно-непрерывная функция времени (например, кусочно-линейная).
Такой вид представления модели позволяет использовать методы параметрической идентификации, например метод наименьших квадратов, реализованный в System Identification Toolbox в MATLAB. В качестве параметров функции ident используются исследуемый {yk} (output) и сгенерированный кусочно-непрерывный ряд {![]() } (input). Выходом функции является матрица A, В, C найденных размерностей. Заметим, что размерность пространства состояний, полученных в результате идентификации системы, всегда равна численным оценкам первоначально реконструированного аттрактора.
} (input). Выходом функции является матрица A, В, C найденных размерностей. Заметим, что размерность пространства состояний, полученных в результате идентификации системы, всегда равна численным оценкам первоначально реконструированного аттрактора.
Здесь хаос генерируется как периодическое изменение линейной траектории, не дающей динамике прийти к устойчивой или периодической траектории. Конечно, не во всех приложениях такие модели представляются удобными, но для систем управления использование вида (5) позволяет использовать известные методы синтеза и оценок параметров. Кроме того, для инженерных задач, обеспечения безопасности информационных систем, где широко используются хаотические сигналы, данный метод позволяет генерировать робастный хаос с заданными свойствами (вид аттрактора, степень нарушения симметрии и др.).
Для примера приведем вид моделей, полученных для системы теплообмена [6]:
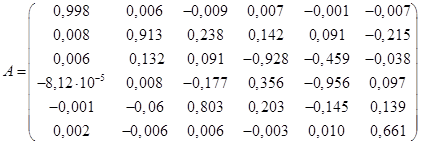 ;
;
![]() ;
;
![]() .
.
Сравнение моделируемого выходного процесса с реальными данными показано на рис. 4. Видно, что модель демонстрирует сложное динамическое поведение, адекватное рассматриваемому теплообменному процессу. На рис. 5 показано сравнение сгенерированного по построенной модели графика переходных процессов во времени для решения задачи оптимального быстродействия.
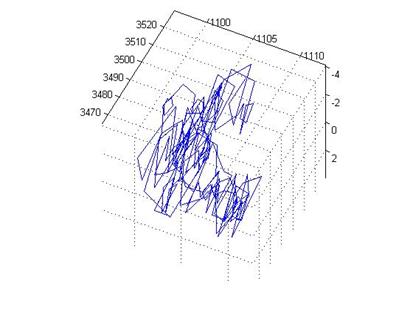
Рис. 4. Реконструированный фазовый портрет
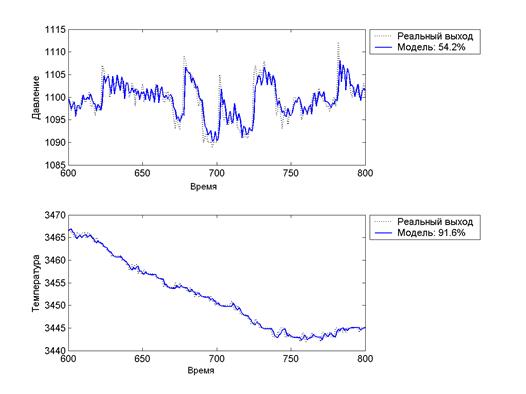
Рис. 5. Сравнение динамики реальной системы и ряда, сгенерированного
по построенной модели
Полученные модели использованы для синтеза управления с учетом нескольких критериев качества, и результаты были внедрены при управлении реальной системой теплообмена (функционировала около 10 лет), что свидетельствует о надежности подхода.
Заключение
Разработан метод построения математических моделей хаотических процессов. Полученные модели могут быть использованы для построения робастного хаоса [22], а также для генерации хаоса с заданными качественными свойствами.
Существует широкое использование хаотических моделей для моделирования систем обмена данных в компьютерных сетях, сформирован экспериментальный стенд для разработки систем управления обменом данных [10]. При использовании протоколов TCP/IP в системах обмена данных возникают фрактальные явления. Использование динамических моделей хаотических процессов позволяет обеспечивать прогнозное упреждающее управление для динамического распределения ресурсов в сложных инфраструктурах. При этом важной задачей является выбор формы модели. Использование предложенной формы позволит получить вычислительно надежные модели, которые, с одной стороны, отражают необходимые качественные свойства нелинейных систем, с другой — не чувствительны к незначительному изменению параметров.
Рецензенты:
Горяшко А.П., д.т.н., профессор, профессор кафедры информатики и автоматизации Московского технологического института, г. Москва.
Пылькин А.Н., д.т.н., профессор, декан факультета вычислительной техники, заведующий кафедрой вычислительной и прикладной математики Рязанского государственного радиотехнического университета, г. Москва.



