Роевой интеллект описывает коллективное поведение децентрализованной самоорганизующейся системы и рассматривается в теории искусственного интеллекта как метод оптимизации [4]. Системы роевого интеллекта состоят из множества агентов, взаимодействующих между собой и с окружающей средой. Сами агенты следуют достаточно простым правилам, но их случайные взаимодействия приводят к возникновению интеллектуального глобального поведения, неконтролируемого отдельными особями.
Алгоритмы роевого интеллекта относятся к классу эвристических алгоритмов. Эвристический алгоритм - это алгоритм, предназначенный для более быстрого решения проблемы по сравнению с классическими методами, или для нахождения приближенного эффективного решения, когда другие методы не в состоянии найти точное решение [2]. Это достигается за счет оптимальности, полноты, точности или скорости выполнения алгоритма.
Целью данного исследования является изучение эффективности работы алгоритма поиска косяком рыб в рамках решения задачи глобальной оптимизации.
Алгоритм поиска косяком рыб (Fish School Search, FSS) был предложен в 2008 г. Б. Фило и Л. Нето. Основными составляющими алгоритма являются движение агента, его поведение и поведение косяка рыбы, которое зависит от двух операторов – кормления и плавания.
Материалы и методы исследования
Каждый агент отличается собственной памятью, где хранится информация о его весе и лучшем положении. Алгоритм предусматривает, что у отдельной рыбы вес ограничивается максимальным значением, начальное значение фиксируется как половина максимального значения. Количество пищи в новом положении используется для вычисления нового веса в соответствии с уравнением
, (1)
где t - время (в рассматриваемом случае это число итераций) , i - количество агентов, 
- вес агента, 
- позиция i-го агента и 
- значение целевой функции в i-й позиции [2].
Оператор плавания можно разделить на следующие составляющие: индивидуальное движение, коллективно-инстинктивное движение и коллективно-волевое движение.
Индивидуальное движение порождает новую позицию для дальнейшего исследования. Каждый агент принимает решение о виде отдельного движения; направление движения генерируется в случайном порядке. Длина пути определяется в зависимости от величины отдельного шага. Значение фитнес-функции рассчитывается исходя из положения, которое приобретает агент, когда он занимает новую позицию. Новое положение заменяет предыдущее, если приобретенная позиция лучше.
Направление и длину коллективно-инстинктивного движения определяет уравнение
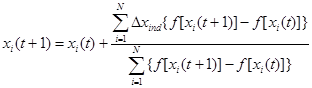, (2)
где N - количество рыб в косяке и 
- изменение позиции i-го агента во время его индивидуального движения [5].
Уравнение показывает, что направление и длина пути максимально зависят от наиболее эффективных агентов в косяке. Весь косяк движется к набору самых успешных рыб.
Коллективно-волевое движение собирает всех особей в косяк, если движение основополагающих рыб косяка было эффективным. В противном случае косяк распространяется по всей предложенной территории. Вес показывает, насколько эффективен косяк рыб: если вес увеличивается - косяк успешен, и новые позиции задает следующее уравнение
, (3)
Если вес уменьшается, то косяк не успешен; новые позиции определяются уравнением
, (4)
где rand - случайное число в интервале (0,1) и функция B(t) вычисляется как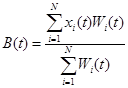 
(5)
Исследование эффективности работы алгоритма поиска косяком рыб было проведено на примере задачи глобальной оптимизации; в качестве критериев эффективности были выбраны скорость и точность работы алгоритма.
Таблица 1
Влияние размера популяции на время выполнения алгоритма
|
Размер популяции |
5 |
7 |
10 |
25 |
28 |
35 |
45 |
50 |
|
Время выполнения алгоритма (мс) |
30 |
31 |
30 |
29 |
30 |
32 |
34 |
30 |
Исследование влияния размера популяции на время выполнения алгоритма осуществлялось на примере поиска экстремума функции 
, наиболее эффективные значения представлены в таблице 1. Из нее видно, что оптимальный размер популяции – 25 особей.
Для изучения зависимости скорости поиска решений от значения максимального веса агента была выбрана функция 
. Результаты исследований отображены в таблице 2.
Таблица 2
Влияние максимального веса агента на время выполнения алгоритма
|
Вес агента |
3 |
5 |
7 |
10 |
13 |
15 |
20 |
30 |
|
Время выполнения алгоритма (мс) |
50 |
50 |
48 |
51 |
54 |
59 |
53 |
47 |
В таблице 3 показано влияние количества итераций на точность и время выполнения алгоритма.
Таблица 3
Влияние количества итераций на точность и время выполнения алгоритма
|
Количество итераций |
25 |
50 |
75 |
100 |
150 |
200 |
250 |
500 |
1000 |
|
Точность выполнения алгоритма (%) |
75 |
86 |
91 |
91 |
88 |
95 |
98 |
100 |
86 |
|
Время выполнения алгоритма (мс) |
27 |
28 |
37 |
43 |
43 |
54 |
50 |
54 |
93 |
Для сравнительного анализа эффективности работы алгоритма поиска косяком рыб в рамках решения задачи глобальной оптимизации были выбраны следующие методы: генетический алгоритм (ГА), метод наискорейшего спуска и метод Ньютона.
В процессе проведения исследований был разработан программный модуль, основное окно которого представлено на рисунке 1 [1; 3]. Он позволяет производить поиск глобального экстремума для нескольких функций: Де Джонга, Растригина и Розенброка.
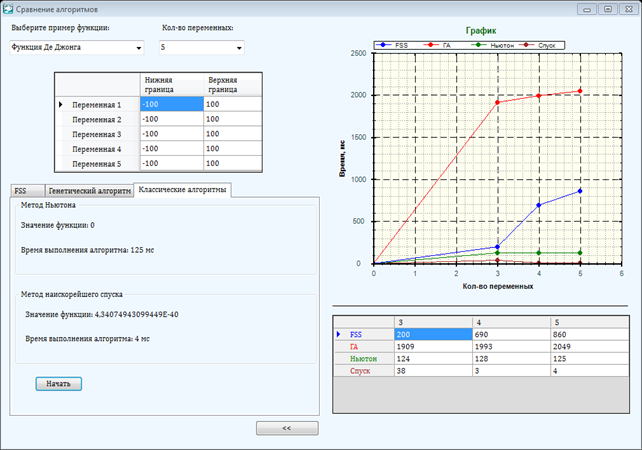
Рис. 1. Основное окно программного модуля.
На рисунке 2 изображен график зависимости количества итераций, необходимых для нахождения оптимума функции Де Джонга с различным числом переменных.
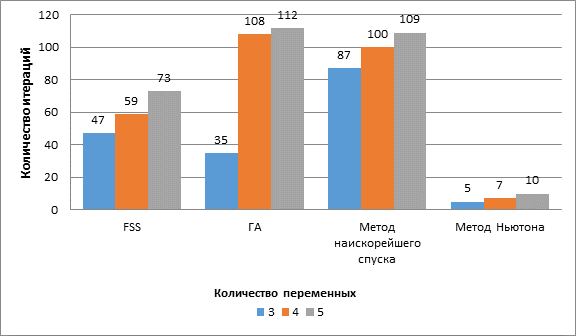
Рис. 2. Количество итераций для поиска оптимума функции де Джонга с различным числом переменных.
В таблице 4 приведены результаты вычисления значений оптимума функции Де Джонга с различным количеством переменных.
Таблица 4
Точность найденного решения исследуемыми алгоритмами для функции Де Джонга
|
Количество переменных |
3 |
4 |
5 |
|
FSS |
<0,0001 |
0,1 |
0,15 |
|
ГА |
0,03 |
0,015 |
0,014 |
|
Метод н. спуска |
0,0015 |
<0,0001 |
0,0004 |
|
Метод Ньютона |
<0,0001 |
<0,0001 |
<0,0001 |
В таблице 5 и 6 представлены зависимости количества итераций, необходимых для нахождения оптимумов функций Розенброка и Растригина соответственно.
Таблица 5
Количество итераций для функции Розенброка с различным числом переменных
|
Количество переменных |
3 |
4 |
5 |
|
FSS |
52 |
111 |
304 |
|
ГА |
37 |
144 |
395 |
|
Метод н. спуска |
12505 |
12524 |
12612 |
|
Метод Ньютона |
98 |
130 |
214 |
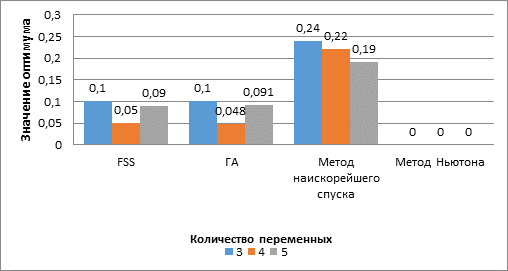
Рис. 3. Точность найденного оптимума функции Розенброка с различным числом переменных.
Таблица 6
Количество итераций для нахождения оптимума функции Растригина с различным числом переменных
|
Количество переменных |
3 |
4 |
5 |
|
FSS |
81 |
120 |
284 |
|
ГА |
73 |
147 |
376 |
|
Метод н. спуска |
16 |
17 |
20 |
|
Метод Ньютона |
2 |
4 |
5 |
Таблица 7
Точность найденного решения исследуемыми алгоритмами для функции Растригина с различным числом переменных
|
Количество переменных |
3 |
4 |
5 |
|
FSS |
0,05 |
0,051 |
0,054 |
|
ГА |
0,05 |
0,056 |
0,048 |
|
Метод н. спуска |
21 |
37 |
54 |
|
Метод Ньютона |
75 |
100 |
125 |
По результатам проведенных исследований можно сделать вывод, что генетический алгоритм и алгоритм поиска косяком рыб являются универсальными методами для нахождения оптимума функций любой сложности. Однако для поиска оптимума простых функций эффективнее использовать классические методы, так как они работают немного быстрее ГА и FSS.
В качестве практической реализации алгоритма поиска косяком рыб можно выделить задачу оптимизации движения квадрокоптеров.
Квадрокоптер — это летательный аппарат, состоящий из рамы, четырех винтов с двигателями и блоком управления; он имеет несколько преимуществ по сравнению с вертолетом - движется по воздуху, изменяя обороты двигателей, поэтому ему не нужен главный ротор наклона [6].
При адаптации алгоритма FSS к решению данной проблемы необходимо принять во внимание особенности движения квадрокоптеров: если один агент изменяет направление движения, то остальные квадрокоптеры также должны поменять траекторию полета. Основным компонентом защиты от столкновений является двойная зона безопасности вокруг каждого квадрокоптера. Зона безопасности имеет цилиндрическую форму: внутренняя зона ограничивает область, в которую квадрокоптеры не могут влетать, она также позволяет избежать столкновений и взаимных помех от воздушного потока из роторов. Внешняя зона безопасности аналогично представляет собой цилиндрическую форму, размер этой зоны используется для вычисления траектории агентов косяка. Внешняя зона безопасности может быть нарушена в ходе реального полета. Это дает достаточно места для тормозного пути и для колебаний квадрокоптера вокруг целевой позиции.
Выводы
При анализе работы алгоритма поиска косяком рыб для нахождения оптимума функций видно, что FSS является универсальным методом для поиска экстремума независимо от сложности функций. Для поиска оптимума достаточно простых функций предпочтительнее использовать классические методы, так как они в данном случае работают немного быстрее эвристических алгоритмов. При решении задачи глобальной оптимизации для функции со сложным ландшафтом рекомендуется использовать FSS, так как классические алгоритмы зачастую приводят к неверному решению, а генетический алгоритм, как можно заметить, работает медленнее.
Рецензенты:
Ключко В.И., д.т.н., профессор, профессор кафедры ИСП Кубанского государственного технологического университета, г. Краснодар.
Видовский Л.А., д.т.н., зав. кафедрой ИСП Кубанского государственного технологического университета, г. Краснодар.