Анализ публикаций в специализированных журналах Mechanism and Machine Theory, Automatica, Robotics and Autonomous Systems, Intelligent Autonomous Systems, Mechatronics, Control Engineering Practice [4, 5, 8, 9] за последнее десятилетие показывает, что усилия многих исследовательских лабораторий в области робототехники направлены на построение автономных коллективов роботов и решение связанных с этим специфических задач. Это может быть обосновано тем, что при использовании роботов для решения новых задач, не связанных с промышленным производством [3] и подразумевающих «самостоятельное» их функционирование в течение продолжительного времени, коллективные решения по сравнению с одиночным роботом отличаются большей эффективностью, низкой стоимостью, высокой надежностью и устойчивостью к внешним возмущениям.
Одной из ключевых задач при функционировании роботов в недостаточно известной обстановке является планирование безопасных траекторий, позволяющих строить гладкие безаварийные маршруты перемещения. Сложность синтеза траекторий для коллективов роботов состоит в том, что, во-первых, в рабочей зоне присутствуют другие мобильные роботы (подвижные препятствия), движение которых в большинстве случаев рассматривается как случайный процесс с неизвестными параметрами, а во-вторых, вычислительные возможности бортовых систем мобильных роботов ограничены, что не позволяет решать задачу планирования с использованием классических переборных или потенциальных алгоритмов.
Поэтому большая часть публикаций в приведенных выше журналах представляет собой различные способы использования интеллектуальных алгоритмов, построенных с использованием нейронных сетей (НС), нечетких или генетических алгоритмов [1]. Эффективность определенного числа решений достаточно спорна, но несомненным является их преимущество в скорости расчета. В связи с вышесказанным, синтез нейросетевой системы планирования, с учетом специфики решаемой задачи и аппаратных возможностей мобильных мини-роботов, представляется актуальной и своевременной задачей.
«Классические» способы решения задачи поиска траекторий
Задача поиска траектории для агента коллектива роботов – сложная и нетривиальная задача, поэтому существует множество алгоритмов, позволяющих решать подобные задачи в соответствии с заранее заданными критериями качества решения. Большая часть этих алгоритмов являются модификациями «базовых» методов планирования пути, оптимизированных под определенные условия. Алгоритмы поиска пути можно разделить на 3 уникальных группы:
-
алгоритмы обхода препятствий;
-
методы поиска пути по графу;
-
интеллектуальные алгоритмы.
Основная задача при поиске траектории робота в окружающем пространстве – это обход препятствий, и достаточно часто, для повышения скорости расчета пути и перемещения, препятствия игнорируются вплоть до столкновения с ними или до входа в зону безопасности. Этот подход достаточно часто применяют, так как для его функционирования необходимо знать только относительные координаты робота и его цели и своевременно выявлять признаки блокирования пути препятствием.
К классическим поисковым алгоритмам относятся как простейшие «перемещение в случайном направлении» или «трассировка вокруг препятствия», так и более функциональные, такие как «надежная трассировка» или «эффективная взвешенная траектория». Реализуемые на их базе системы планирования не всегда способны найти траекторию в сложно организованном пространстве, проблему представляют невыпуклые препятствия, различного рода карманы, уступы и тупики. Большинства из перечисленных недостатков не наблюдается при использовании алгоритмов поиска пути по графу, которые планируют все перемещения до момента начала движения.
В робототехнике часто используют такие алгоритмы поиска по графу, как классические: «поиск в ширину», его более быстрая модификация – «двунаправленный поиск в ширину» и «алгоритм Дейкстры», так и их более глубокие модернизации – «поиск в глубину (DFS)», «Алгоритм последовательных приближений при поиске в глубину (IDDFS)», «лучший-первый» и т.д. Высокой эффективностью при поиске путей близких к оптимальным по графу является алгоритм A*, который пошагово просматривает все пути, ведущие от начальной вершины в конечную, пока не найдёт минимальный. При этом алгоритм просматривает сначала те маршруты, которые «кажутся» ведущими к цели, при этом он корректно сочетает в себе такие свойства, как учет длины предыдущего пути (алгоритма Дейкстры), так и эвристику из алгоритма «лучший-первый».
Среди интеллектуальных методов поиска траекторий особое внимание заслуживают генетические алгоритмы и нейросетевые реализации систем планирования. Впервые использование нейронных карт для решения такого рода задач было предложено в работе Michail G. Lagoudakis «Mobile robot local navigation with a Polar Neural Map», где предлагалась система позиционирования для одного мобильного робота (МР) [7]. Суть метода состоит в том, что рекуррентная НС Хопфилда используется как топологическое представление дискретного рабочего пространства, т.е. центру каждой дискретной ячейки соответствует нейрон, связанный лишь со своими ближайшими соседями, причем связи с соседями имеют вес соответствующий длине. Далее НС передается входной вектор начального состояния, в котором нейроны, соответствующие ячейкам-препятствиям, имеют неизменное нулевое состояние, ячейка-цель имеет максимальное значение и равна 1. После завершения процесса активации, т.е. достижения условия, когда все нейроны, кроме нулевых, примут значение отличное от нуля – формируется матрица состояния всех нейронов сети (нейронная карта), причем размерность матрицы соответствует размерности дискретного рабочего пространства. Метод получения нейронной карты основан на эффекте «самоорганизации», используемый в сетях Кохонена [6]. Используя алгоритм градиентного поиска по матрице состояний, возможно формирование пути, близкого к оптимальному.
Система планирования траектории с помощью нейронной карты
Как было сказано выше, основная идея предлагаемого метода планирования траекторий состоит в том, чтобы использовать нейронную карту как динамическое представление рабочего пространства. Информация о конфигурации рабочего пространства, необходимая для создания карты, поступает с внешних источников (например, от сенсорной системы или информационного сервера). Энергетические взаимодействия нейронов в сети через подобные волновому распространению процедуры приводят к тому, что нейроны принимают постоянное значение энергии на всем пространстве состояний, то есть сеть входит в состояние устойчивости после завершения активации. Если выходной вектор сети в состоянии устойчивости представить в виде матрицы, размерность которой совпадает с топологическим построением сети, то мы получим в конечном итоге нейронную карту, которая может быть использована как навигационная карта для расчета траектории в заданном пространстве.
Система планирования траектории базируется на двух главных компонентах: нейронная карта и конструктор пути. Система работает следующим образом: координаты цели, а также информация об окружающей среде с сенсорной системы поступают на вход нейронной сети Хопфилда. Нейроны в сети в результате энергетических взаимодействий входят в состояние равновесия и принимают собственные значения энергии (в зависимости от функции активации). Энергетические взаимодействия в сети обусловлены динамикой и архитектурой самой сети, а также конфигурацией окружающего пространства и координатами цели, которая является точкой активации. Устойчивые значения энергии нейронов на данной нейронной области формируют «нейронную карту», которая подается на вход блока конструктора пути, формирующего, в свою очередь, конечную траектории [7].
Непосредственное влияние на формирование нейронной карты (и, следовательно, работы всей системы в целом) оказывает структурная организация связей между нейронами, то есть топология сети.
Рассмотрим нейронную сеть Хопфилда с n нейронами. Все нейроны сети находятся в нулевом состоянии, и не имеется никаких источников входных сигналов. Тогда нейроны будут размещены в d-размерной решетке, равномерно распределенной по заданному пространству С, где d – размерность С. Таким образом, нейронная сеть и созданная нейронная карта служат дискретным топологическим упорядоченным представлением С. Топология распределения и подключения нейронов в сети может меняться. На рис. 1 показаны различные топологии сети для двумерного пространства.

Рис. 1. Возможные топологии сети для 2-х мерного пространства
Каждый элемент i соответствует подмножеству Ci заданного пространства С, объединение всех ячеек Ci создает полную поверхность C. Для создания нейронной карты необходимо, чтобы распространение энергии в сети было подобно эффекту распространения волны, поэтому каждый нейрон i взаимодействует только с соседними в пределах своего подмножества Ci. Следовательно, каждый нейрон в сети имеет связи лишь с коротким диапазоном (прямые или диагональные) с симметричным распространением.
Сети, способные к самоорганизации, используют методы обучения «без учителя». НС Хопфилда обучается по правилу (алгоритму) Хебба, которое полагает, что синаптическая связь, соединяющая два нейрона, будет усиливаться, если в процессе обучения оба нейрона согласованно испытывают возбуждение, либо торможение [2].
Таким образом, энергетическая динамика выбранной в качестве базы НС Хопфилда позволяет при подаче на вход определенного набора данных самостоятельно сформировать желаемый «образ» (нейронную карту). Если по значениям нейронной карты построить поверхность, то она будет иметь вид «возвышенности» с пиком в точке активации (рис. 2):
а) 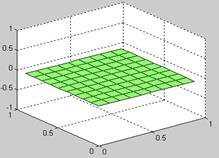 б)
б) 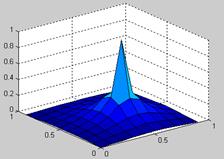
Рис. 2. Поверхность активации НС: а) начальное (нулевое) состояние сети; б) активированная сеть
Дальнейшую обработку выходного потока данных НС и расчет траектории выполняет отдельная вычислительная подсистема – «конструктор пути».
На первом этапе конструктор пути производит подготовку выходного вектора для расчета траектории: выполняет преобразование выходного вектора в матричную форму в соответствии с топологическим представлением рабочего пространства, т.е. формирует матрицу состояния НС – нейронную карту. В зависимости от начальных знаний о конфигурации рабочего пространства блок конструктора пути может производить расчет полной траектории (конфигурация известна и статична) или же расчет отдельных частей траектории (конфигурация частично неизвестна и динамична).
Основные вычислительные операции блока конструктора пути представляют собой выполнение процедуры поиска в ближайшем окружении и перехода в новый узел сети. Направление перехода на каждом расчетном шаге определяется максимальным градиентом по направлению от текущего значения нейрона i до соседнего нейрона j. Процесс повторяется для j-го нейрона и так далее вплоть до того, пока не будет найден целевой нейрон с максимальным значением энергии и построена конечная траектория [6].
При построении системы расчета траекторий для группы МР в общем рабочем пространстве на конструктор пути также возлагается еще одна ключевая функция – разрешение конфликтных ситуаций с учетом приоритетов и соответствующая динамическая корректировка траекторий.
В зависимости от решаемых задач, а также информационных и вычислительных ресурсов возможны различные подходы к реализации системы планирования для группы МР. Ниже рассмотрим аппаратные и программные особенности построения данной системы при различных подходах.
Выбор основных вариантов реализации системы планирования проводится с учетом следующих основных критериев:
-
вычислительные возможности аппаратной базы;
-
конфигурация рабочей зоны (размер, расположение препятствий);
-
требования к скорости решения задачи позиционирования;
-
требования к энергоемкости (количество затраченных мобильным агентом энергоресурсов на расчет и переход на расстояние, равное единице дискретного рабочего пространства);
-
требования к надежности системы.
Исходя из этих критериев, рассматриваются следующие варианты построения системы планирования:
-
централизованный;
-
гибридный;
-
децентрализованный.
Централизованный подход. Построение системы планирования по централизованному варианту предполагает решение задачи позиционирования группы в едином центре, то есть размещение всех вычислительных функций системы в общем центральном блоке (ЦБ). ЦБ по имеющейся информации о конфигурации рабочего пространства выполняет формирование нейронных карт для каждого из агентов, а также расчет траекторий с учетом скоростей и разрешение возможных конфликтных ситуаций. Стоит также отметить, что вычислительные операции НС и конструктора пути (КП) для каждого агента выполняются параллельно в отдельных потоках с доступом к общим программным ресурсам. Агенты, в свою очередь, лишь принимают по каналам данных управляющие сигналы и в соответствии с ними приводят в действие исполнительные механизмы, то есть безоговорочно выполняют «указания» центра [3].
Реализация системы планирования по централизованному подходу представлена на рис. 3.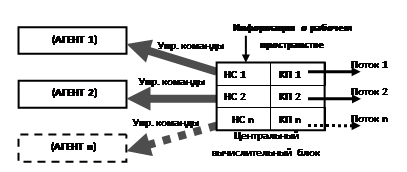
Рис. 3. Структурная схема системы планирования траектории с общим центральным вычислительным блоком
Гибридный подход. При применении гибридного подхода система планирования реализуется с общим блоком конструктора пути и распределенной НС Хопфилда. В данном исполнении каждый из агентов оснащается вычислительным блоком НС, формирует собственную нейронную карту и производит ее динамическую корректировку по начальным данным и сенсорной информации о рабочем пространстве. Сформированную нейронную карту агент по каналу связи передает в общий вычислительный блок, который запускает процесс расчета траектории в отдельном потоке и выдачу управляющих сигналов. Управляющие команды ЦБ не подлежат к обязательному исполнению агентом, так как в процессе движения агент может получать новые «знания» о рабочей зоне и в соответствии с ними корректировать нейронную карту. После обновления карты агент передает эти данные в центральный конструктор пути, который (при необходимости) производит асинхронную коррекцию траектории от текущего местоположения. Принцип реализаций системы планирования по гибридной схеме представлен на рис. 4.
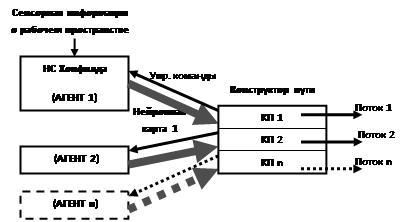
Рис. 4. Структурная схема системы планирования траектории с центральным блоком конструктора пути и распределенной НС Хопфилда
Децентрализованный подход. При реализации системы планирования по децентрализованной схеме каждый агент имеет собственную систему расчета траектории с вычислительным блоком НС и конструктором пути. Во время выполнения задачи группового позиционирования агенты, приобретая новые «знания» об окружающем пространстве, обмениваются данным с ближайшим окружением по каналам связи. На основании полученной глобальной информации агенты самостоятельно корректируют свои траектории и разрешают конфликтные ситуации. Реализация децентрализованной системы планирования траекторий представлена на рис. 5.
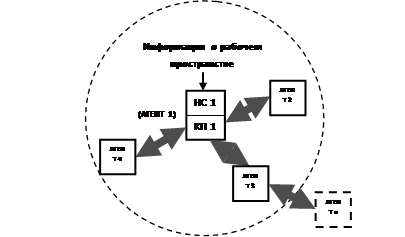
Рис. 5. Структурная схема распределенной системы планирования траектории
Результаты моделирования алгоритма группового управления
Исходя из указанных критериев, определяющих выбор того или иного подхода к построению системы планирования, в рамках научно-исследовательской работы в качестве основной схемы реализации системы была выбрана централизованная схема. Данный принцип построения имеет ряд ключевых преимуществ, определяющих его актуальность в качестве основного подхода к построению системы для отработки алгоритма группового управления:
-
легкость расширения аппаратных ресурсов всей системы в широком диапазоне за счет увеличения вычислительных возможность центрального блока (по сути, обычного ПК);
-
минимальные требования к аппаратным возможностям агентов, что значительно удешевляет систему и расширяет возможности применения (актуальность вопроса экономической целесообразности и аппаратных возможностей агентов возрастает с увеличением количества агентов в группе, а также при уменьшении размеров самих агентов);
-
скорость и надежность обработки конфликтных ситуаций за счет разделяемого доступа к общим аппаратным ресурсам.
Очевидным недостатком централизованной схемы управления является «живучесть», т.к. выход из строя ЦБ ведет к выходу из строя всей системы. Тем не менее возможно частичное решение данной проблемы за счет резервирования ЦБ путем организации кластера высокой доступности.
На рисунках ниже представлены результаты моделирования централизованной системы планирования траекторий для группы из 3-х агентов (рис. 6, 7).
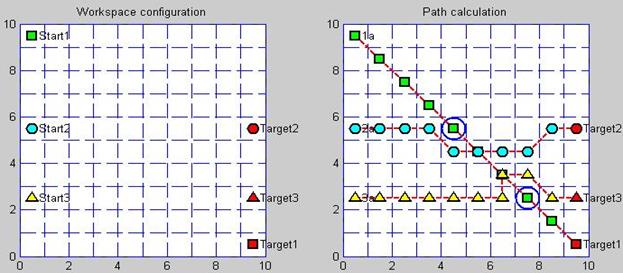
Рис. 6. Результат работы системы планирования при взаимном пересечении траекторий агентов
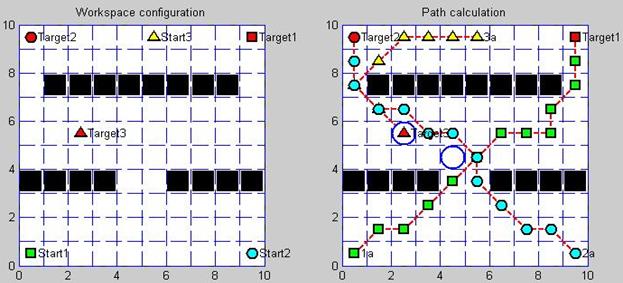
Рис. 7. Результат работы системы планирования при взаимном пересечении траекторий агентов и обходе препятствий
Как видно из рисунков, система планирования корректно строит траектории и разрешает конфликтные ситуации (конфликтные области обозначены окружностями) для всех участников группы.
Выводы
Подводя итог статьи, можно сделать следующие выводы:
1) Несмотря на достаточно высокую эффективность классических методов поиска пути, интеллектуальный алгоритм планирования на базе НС Хопфилда (метод «нейронных карт») имеет следующие преимущества:
-
производительность, которая характеризуется быстрой обработкой рабочего пространства за счет особенностей топологии и активационной динамики НС;
-
гибкость применения, которая обеспечивается четким разделением всего процесса решения задачи позиционирования на два основных этапа: представление рабочего пространства (формирование нейронной карты) и расчет пути, что позволяет синтезировать на базе данного метода алгоритм управления группой МР.
2) Выбор схемы реализации системы планирования во многом определяется имеющейся аппаратной базой, требованиями к надежности, а также условиями решения общей задачи позиционирования группы, в частности: скорость решения задачи, необходимость и (если необходимо) оперативность реакции на динамические возмущения окружающей среды, продолжительность автономной работы и конфигурация общей рабочей зоны.
3) Исходя из заданных критериев, централизованный подход к реализации системы планирования является наиболее приемлемым для синтеза и отработки алгоритма взаимодействия участников группы роботов. Эффективность алгоритма группового управления была подтверждена в ходе экспериментального моделирования.
Авторы выражают благодарность Программе фундаментальных исследований № 1 ОЭММиПУ РАН «Научные основы робототехники и мехатроники» за финансовую поддержку проводимых исследований.
Рецензенты:
Мунасыпов Р.А., д.т.н., профессор, заведующий кафедрой «Мехатронные станочные системы», ФГБОУ ВПО Уфимский государственный авиационный технический университет, г. Уфа.
Жернаков С.В., д.т.н., профессор, заведующий кафедрой «Электроника и биомедицинские технологии», ФГБОУ ВПО Уфимский государственный авиационный технический университет, г. Уфа.



