Проблема формализации знания. В современной литературе отмечается, что формализация эпистемических контекстов стала потребностью во многих областях современной науки: информатике, экономике, лингвистике, эпистемологии. Мы полагаем, что проблема формализации знания в эпистемических модальных системах является лишь показателем того, что модальные системы не учитывают важнейших пресуппозиций, которые подразумеваются в утверждениях вида (1) «N знает, что А», (2) «N не знает, что А», (3) «N верит, что имеет место А», (4) «N не верит, что имеет место А». В настоящее время не существует единого взгляда на то, какое сочетание качеств наилучшим образом подходит для приемлемой во всех отношениях характеристики познающего субъекта.
Далее мы будем пользоваться термином рациональный агент для обозначения субъекта знания, обладающего знанием логических законов и правил вывода, а также способного строить логические следствия из известного ему знания. При этом рациональным агентом является любая система, обладающая вышеназванными качествами (таким образом рациональным агентом может быть как человек, так и компьютер).
Моделирование эпистемических свойств рациональных агентов в качестве теоретического основания должно иметь формальную теорию знания – специализированную для этой цели эпистемическую логику. Подобные эпистемические системы начали строиться в середине прошлого века, в настоящее время существует множество различных эпистемических систем, формализующих контексты знания. Однако идеализации, использовавшиеся при построении этих систем, оказались слишком сильными для того, чтобы дать адекватную формализацию рассуждений рациональных агентов [4]. Данные идеализации не учитывают ряд особенностей рациональных агентов, таких как ограниченность во времени, т.е. не способность получать мгновенно все следствия из имеющихся знаний, необходимость в т.н. ментальных усилиях, агент должен думать, чтобы получить следствия, должен знать правила вывода и порядок их применения. Для устранения проблем формализации знания и их причин, на наш взгляд, потребуется построение такой эпистемической системы, которая будет отражать основные пресуппозиции подобных высказываний.
Наиболее подходящей системой, удовлетворяющей основные выделенные нами требования к формализации эпистемических контекстов является динамическая эпистемическая логика [9], построенная на базе модальной логики и дополненная оператором времени, учитывающим одновременно знание агентом правил вывода.
1. Эпистемическая логика
1.1 Язык эпистемической логики К.
Алфавит модальной эпистемической логики:
-
Множество пропозициональных переменных Р: р, q, r, s, p1, q1, r1, s1, p2, и т.д.
-
Логические связки ¬, &, v,
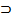 .
.
-
Эпистемический модальный операторК (агент i знает, что).
-
Технические символы( , ), , .
Модальный оператор К снабжается нижним индексом i, обозначающим агента знания. Соответственно, КiА (где А любая формула) следует читать как «агент i знает, что А».
Формула определяется индуктивно:
-
Любая пропозициональная переменная есть формула.
-
Если А и В формулы, то ¬А, А&В, АvВ, А
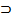 В, КаА – формулы.
В, КаА – формулы.
1.2 Аксиомы модальной эпистемической логики
Система К.
-
Любая аксиоматизация пропозиционального исчисления.
-
К (
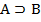 )
) 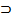 (К
(К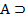 КВ) – аксиома К.
КВ) – аксиома К.
Система Т.
-
Аксиомы системы К.
-
КА
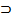 А – аксиома Т.
А – аксиома Т.
Система S4.
-
Аксиомы системы Т.
-
КА
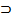 ККА – аксиома S4.
ККА – аксиома S4.
Система S5.
- Аксиомы системыS4.
- ¬КА
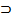 К¬КА – аксиома S5.
К¬КА – аксиома S5.
Аксиомы модальных доксастических систем.
-
К(
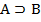 )
) 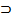 (К
(К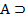 КВ) – аксиома К.
КВ) – аксиома К.
-
¬К(А&¬А) – аксиома D.
-
КА
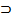 ККА – аксиома S4.
ККА – аксиома S4.
-
¬КА
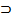 К¬КА – аксиома S5.
К¬КА – аксиома S5.
Правила вывода для всех систем одинаковы:
- Правило modusponens.
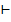 А
А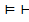 КА правило модализации.
КА правило модализации.
В дальнейшем также возможно использование производного правила вывода
![]() (
(![]() )
) ![]() К
К![]() КВ– правила монотонности.
КВ– правила монотонности.
1.3 Проблема логического всеведения
За основу эпистемической логики принимается модальная пропозициональная логика. В модальной логике оператор: « » читается как «необходимо, что», и сама логика является логикой необходимости. В эпистемической логике аксиомы модальной логики получают иное прочтение, что и приводит к парадоксу логического всеведения
» читается как «необходимо, что», и сама логика является логикой необходимости. В эпистемической логике аксиомы модальной логики получают иное прочтение, что и приводит к парадоксу логического всеведения
(1) ![]() А
А![]()
 А (если доказуемо А, то доказуемо, что необходимо А),
А (если доказуемо А, то доказуемо, что необходимо А),
(2) ( (
( ![]() )
) ![]()

![]()
 В (если необходимо (А
В (если необходимо (А![]() В) и необходимо А, то необходимо В).
В) и необходимо А, то необходимо В).
В модальном исчислении эти положения не приводят к проблеме всеведения, так как в нем вообще не учитывается знание субъекта. Но когда оператор необходимости трактуется как оператор знания, мы сталкиваемся с проблемой:
(3) читается: «если доказуемо А, то доказуемо, что агент N знает А», т.е. из доказуемости следует знание субъектом всех доказуемых истин;
(4) читается: «если агент N знает (А![]() В) и агент N знает А, то агент N знает В»,
В) и агент N знает А, то агент N знает В»,
т.е. из знания одних высказываний следует знание всех их логических следствий.
Принятие положений (7) и (8) в эпистемической логике приводит к так называемому логическому всеведению:
- субъект познания знает все логические законы;
- субъект познания знает все логические следствия из логических законов;
- субъект познания знает все логические следствия из имеющихся у него самого знаний.
Таким образом, в эпистемической модальной логике встает вопрос о возможности применения некоторых правил и аксиом пропозициональной модальной логики.
Проблема логического всеведения и последствия ее устранения
Мы проанализировали разные эпистемические модальные системы в [1], однако все они страдают, по крайней мере, от одной из двух проблем:
- Субъект познания обладает всеми или некоторыми вариантами логического всеведения;
- Эпистемическая система не отражает способности субъекта строить логические выводы, не учитывает рациональность субъекта; под термином «рациональность субъекта» понимается не разумность субъекта, а его способность строить выводы из имеющегося знания.
Вторая проблема появляется в результате устранения первой. При попытке решить проблему логического всеведения в эпистемических системах теряются свойства рациональности субъекта познания. Следует сказать, что это слишком дорогая цена решения вопроса, ведь агент тогда хоть и не обладает всеведением, но и не «способен» строить выводы из своего знания.
Таким образом, сложились две группы эпистемических систем, в одних сохраняется проблема логического всеведения, например, в стандартной эпистемической логике; в других не отражается рациональность субъекта (система невозможных возможных миров Я. Хинтикки, В. Ранталы, странные миры С. Крипке).
2. Динамическая эпистемическая логика
Новизна данного подхода состоит в том, что помимо учета фактора времени в рассуждениях о знании, в нем учитывается также знание агентом правил вывода. В рассуждениях о знании, с нашей точки зрения, присутствует не только логическая составляющая, т.е. правильность построения выводов, но также важно учитывать время, которое требуется агенту для выведения следствия, агент может не обладать всеми необходимыми посылками, система в которой строится вывод может оказаться неразрешимой, и тогда вывод представляет собой творческий процесс, результат которого тем не менее не гарантирован, также важным является ментальное усилие. Так как даже если агент знает все посылки, правила вывода и алгоритм решения задачи, тем не менее он может не продумать, не осуществить решение задачи, и тогда он не будет знать следствие, хотя в большинстве логических систем окажется, что агент знает данное следствие. В динамической системе [9] используется язык модальной эпистемической логики, но к модальному оператору КА «агент а знает, что А» добавляется оператор A, который читается «А истинно после некоторого времени обдумывания агентом i». Формула [Fi]A является сокращением для ¬¬A и читается «агент i всегда знает А». Модальное выражение A можно также понимать как оператор временной логики «в некоторый будущий момент времени», но время в нем является субъективным, т.е. зависимым от агента, его действий. Введение оператора является важным мометном в эпистемической логике, так как помимо учета времени он позволяет учитывать как ментальные усилия агента, так и знание правил вывода и алгоритма построения вывода. Введение подобного оператора является, с нашей точки зрения, интересной попыткой решить проблему логического всеведения и представляет собой наиболее адекватный метод формализации рассуждений о знании в современной логике. Далее динамическая эпистемическая логика строится как расширение эпистемической логики К.
Язык динамической эпистемической логики
Пусть Agent = {1,…,N} – множество агентов и ![]() – язык эпистемической логики. Тогда
– язык эпистемической логики. Тогда ![]() есть минимальное множество такое, что
есть минимальное множество такое, что
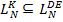 ;
; - если
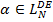 , то
, то 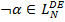 ;
; - если
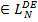 и
и 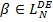 , то
, то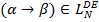 ;
; - если
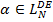 и
и 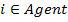 ,
, 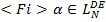
Конъюнкция и дизъюнкция определяются обычным образом. [Fi] α является аббревиатурой для ¬ ¬ α. Формула α читается «то, что α истинна, будет эксплицитно известно агенту i, если у него будет правильный ход мысли», формула [Fi] α читается «то, что α истинна, обязательно будет эксплицитно известно агенту i, при любом ходе его мысли».
Аксиомы и правила вывода
Если В может быть выведено из посылок А1,…,Аm посредством правил R1,…,Rn, тогда соответствующая эпистемическая аксиома будет записываться КiА1&…&КiAmКiB. Таким образом, принимаются следующие схемы аксиом.
Динамическая эпистемическая система К:
1. Аксиомы пропозиционального исчисления.
2. [Fi](A→В)→ ([Fi]А→ [Fi]B) (аксиома временной логики 1).
3. [Fi]A → [Fi] [Fi]А (аксиома временной логики 2).
4. КiА&Кi(A→В) →КiB (аксиома указывает на то, что агент умеет пользоваться правилом modusponens).
5. КiA→ [Fi]КiА (Эта аксиома принимается для сохранения знания агентом некоторой уже полученной формулы, т.е. агент не забывает известных ему формул в процессе рассуждения.)
6. Кi(A→(В→А))
7. Кi((A → (В→С)) → ((A→В) →(А→С)))
8. Кi((¬В→¬А) → (А→В))
Аксиомы 6,7,8 указывают на способность агента пользоваться аксиомами классической логики.
9. [Fi]A → [Fi] А
10. КiA→А (аксиома Т)
11. Кi(КiA→А)
12. КiA → КiКiА (аксиома S4, положительная интроспекция).
Аксиома отрицательной интроспекции ¬КiA →Кi¬КiА не может быть использована, так как на следующем мыслительном шаге формула, которая была не известна, может стать знанием агента.
13. КiА&КiВ →< Fi >Кi(A&B)
14. Кi(A&B) →< Fi >КiА
15. < Fi >Кi(Аv¬А)
16. КiA→¬Кi¬А (аксиома D, вариант аксиомы ¬Кi(А&¬А)).
Правила вывода:
1. Правило modusponens.
2. ⊢А ⊨⊢[Fi]А правило модализации для временной логики.
Принципиальным отличием данной динамической эпистемической логики является наличие оператора , так как за счет его введения устраняются все варианты логического всеведения, но при этом система адекватно отражает способность агентов знания делать выводы и строить доказательства. Но при этом мы не видим принципиального отличия данной системы от системы Бежанишвили М.Н.[3], так как в ней выводы агента не ограничиваются его знанием правил вывода как в динамической эпистемической логике, однако это подразумевается самим набором аксиом, которые представляют собой набор правил вывода, которыми способен пользоваться агент.
В описанном нами варианте динамической эпистемической логики решаются все варианты проблемы логического всеведения, указанные в [8]. Однако выводимой оказывается формула Кi(Аv¬А) и соответственно формула КiАvКi ¬А, которая также является, с нашей точки зрения, вариантом проблемы логического всеведения, так как агент при условии, что он знает правила вывода, и наличии ментального усилия, обязательно будет знать, что А – истинна, либо, что А – ложна. Мы полагаем, что данный вариант проблемы логического всеведения связан с тем, что логика принимаемая в динамической эпистемической логики является двузначной.
Введение истинностно-значных провалов в эпистемическую модальную логику
В семантике возможных миров для эпистемической логики предполагается, что выделяются миры не объективные, образованные логическими возможностями при соблюдении основных законов логики, а миры соответствующие знаниям агентов. Таким образом, в любом варианте построения миров знания эмпирических агентов во всех выделяемых мирах будут появляться высказывания, значения которых агенту не известны. При этом можно выделить два рода таких высказываний: одни из них не известны агенту и не осознаются им (именно относительно такого рода высказываний можно применить принцип Кузанского, согласно которому, чем больше мы познаем, тем больше наше незнание); другие же из них не известны агенту, но осознаются им (так, например, мы можем осознавать высказывание «Множество простых чисел является бесконечным», однако мы не знаем является ли оно истинным). В эпистемической динамической логике введение оператора, соответствующего ментальным усилиям агентов, позволяет ограничить множество миров знания только осознаваемым знанием, т.е. эксплицитным. Поэтому мы принимаем следующее допущение: чем больше возможных миров потребуется для описания знания некоторого агента, тем меньше он знает, а агент, обладающий всеведением, будет иметь только один возможный мир, совпдадающий с актуальным миром.
В случае если агент не знает некоторое высказывание, то он рассматривает пару возможных миров: один, в котором это высказывание истинно, и другой, в котором это высказывание ложно. Но каким будет это высказывание в исходном, актуальном мире? Очевидно, ему должен соответствовать провал в значении, и именно там, где есть провал значения, появляется пара новых возможных миров. Следовательно, для построения логики относительно актуального мира знаний агента требуется введение истинностно-значных провалов. В ином случае значение некоторого высказывания ![]() в актуальном мире знаний агента i, если верно
в актуальном мире знаний агента i, если верно ![]() остается неопределенным и никак не отражается в логике.
остается неопределенным и никак не отражается в логике.
При этом логика будет строиться иначе, чем логика с провалами значений в [3]. Она отличается, во-первых, тем, что принимается иная система аксиом; во-вторых, за основу берется трехзначная логика Клини (К3) с провалами значений, и отказом от принципа исключенного третьего для предложений с провалами значений. В трехзначной эпистемической логике формула Кi(Аv¬А) не является выводимой, таким образом проблема логического всеведения решается в полной мере.
Рецензенты:
Карулин В.П., д.т.н., профессор, ведущий научный сотрудник ФГБНУ «Госметодцентр», Министерство образования и науки РФ, ФГБНУ «Государственный научно-методический центр», г. Москва.
Пьянков В.В., д.т.н., доцент, ведущий научный сотрудник ФГБНУ «Госметодцентр», Министерство образования и науки РФ, ФГБНУ «Государственный научно-методический центр», г. Москва.



