На сегодняшний день в газотурбинных двигателях применяются различные оболочковые конструкции, сопловые и рабочие лопатки турбин, а также элементы камер сгорания, тепловое состояние и работоспособность которых зависит от условий работы систем охлаждения, обеспечивающих теплоотдачу от элемента конструкции к охлаждающему агенту. Сегодня проведены различные исследования газотурбинных двигателей, а именно: в работах Осипова М.И., Веретельник А.В. [3] предложена методика оценки эффективности охлаждения лопаток газотурбинных установок; различные комбинированные покрытия элементов турбин рассмотрены в работах Мошникова А.В., Можайской Н.В. [2].
Актуальность данного исследования обусловлена тем, что обратная задача теплообмена по определению необходимых коэффициентов теплоотдачи во внутренних системах охлаждения газотурбинных двигателей остается нерешенной. Возникающая в процессе работы газотурбинных двигателей неравномерность температуры газа, а также коэффициентов теплоотдачи приводит к неравномерности температур в элементах оболочковых конструкций газотурбинных двигателей. Это снижает надежность ресурсов двигателя. Для выравнивания температур оболочковых элементов газотурбинных двигателей необходимо организовать их охлаждение, обеспечивающее равномерное температурное поле. Для этого нужно распределить охлаждающий воздух и изменить скорость движения, чтобы обеспечивалось необходимое распределение коэффициентов теплоотдачи со стороны охлаждающего воздуха.
Таким образом, рассмотрим задачу по нахождению необходимого распределения коэффициентов теплоотдачи со стороны охлаждающего агента, удовлетворяющих требуемому тепловому режиму. Дифференциальное уравнение теплопроводности в цилиндрической системе координат ![]() с постоянными теплофизическими характеристиками имеет вид [1]:
с постоянными теплофизическими характеристиками имеет вид [1]:
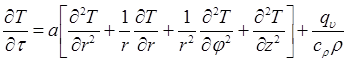 , (1)
, (1)
где Т – температура; τ – время; 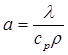 – коэффициент температуропроводности;
– коэффициент температуропроводности; ![]() – коэффициент теплопроводности;
– коэффициент теплопроводности; ![]() – изобарная удельная теплоемкость;
– изобарная удельная теплоемкость; ![]() – плотность;
– плотность; ![]() – объемная мощность внутреннего источника теплоты.
– объемная мощность внутреннего источника теплоты.
Поскольку в задаче рассматривается стационарный процесс ![]() и система не имеет внутренних источников теплоты
и система не имеет внутренних источников теплоты ![]() , уравнение (1) с учетом замены
, уравнение (1) с учетом замены ![]() перепишется в виде:
перепишется в виде:
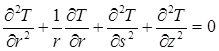 . (2)
. (2)
Представим температуру в виде параболического закона, для того чтобы учесть изменение температуры стенки по радиусу![]() :
:
![]() , (3)
, (3)
где ![]() – текущее значение координаты стенки, отсчитываемое от точки а.
– текущее значение координаты стенки, отсчитываемое от точки а.
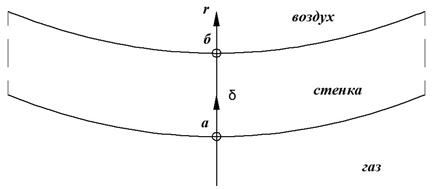
Рис. 1. Элемент оболочки газотурбинного двигателя.
Продифференцируем уравнение (3). Граничные условия определяются условиями теплообмена на внешней стороне оболочки, омываемой газом, и на внутренней стороне, охлаждаемой воздухом. Запишем граничные условия в точке а, учитывая, что![]() :
:
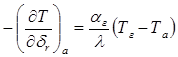 ,
,
где ![]() – коэффициент теплоотдачи со стороны газа,
– коэффициент теплоотдачи со стороны газа, ![]() – температура в точке а,
– температура в точке а, ![]() – температура газа.
– температура газа.
Поскольку ![]() , то
, то 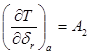 . В результате получаем, что
. В результате получаем, что ![]() Граничное условие в точке б:
Граничное условие в точке б:
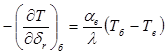 , (4)
, (4)
где ![]() – коэффициент теплоотдачи со стороны газа,
– коэффициент теплоотдачи со стороны газа, ![]() – температура в точке б,
– температура в точке б, ![]() – температура охлаждающего агента.
– температура охлаждающего агента.
Разрешая условие (4), учтем, что для точки б выполняется условие![]() :
:
![]() .
.
Выразим температуру в точке б, используя найденные константы:
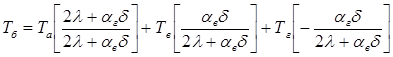 . (5)
. (5)
Используя (5), составим уравнение теплопроводности для стороны оболочки, омываемой газом в точке а, ![]() :
:
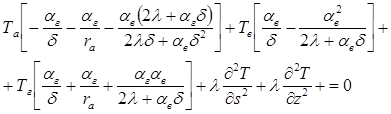 (6)
(6)
Аналогичное нелинейное уравнение теплопроводности для переменных коэффициентов теплопроводности было получено в [4]. Таким образом, основная задача заключается в решении уравнения (6) относительно ![]() . Распределение необходимых коэффициентов теплоотдачи (обозначим как
. Распределение необходимых коэффициентов теплоотдачи (обозначим как ![]() ), должно удовлетворять требуемому температурному полю на поверхности элемента оболочки при заданных условиях работы. Поскольку температура охлаждающего агента на входе в начальной точке известна, получим следующее уравнение для начальной точки:
), должно удовлетворять требуемому температурному полю на поверхности элемента оболочки при заданных условиях работы. Поскольку температура охлаждающего агента на входе в начальной точке известна, получим следующее уравнение для начальной точки:
![]() , (7)
, (7)
где ![]()

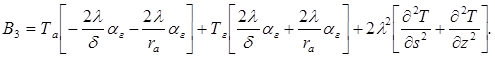
Найдем ![]() в остальных точках по контуру s методом конечных разностей. Для произвольной точки контура выразим
в остальных точках по контуру s методом конечных разностей. Для произвольной точки контура выразим ![]() из (6):
из (6):
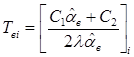 , (8)
, (8)
где 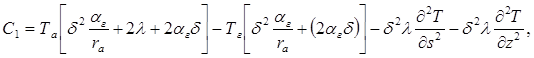
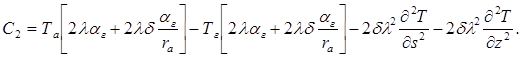
Уравнение подогрева охлаждающего агента при движении от точки ![]() до точки
до точки ![]() рассматриваемой оболочки имеет вид:
рассматриваемой оболочки имеет вид: 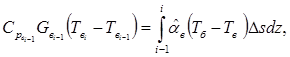 перепишем его приближенном виде:
перепишем его приближенном виде:
![]() , (9)
, (9)
где ![]() – расход воздуха через одну лопатку.
– расход воздуха через одну лопатку.
Подставим (8) в выражение (9) и запишем уравнение относительно требуемого коэффициента теплоотдачи ![]() :
:
![]() , (10)
, (10)
где 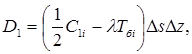
![]()
![]()
Решая (10), можем определить ![]() . Значение
. Значение ![]() получим, используя соотношение:
получим, используя соотношение:
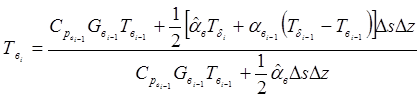 . (11)
. (11)
Таким образом, последовательно находим значения коэффициентов теплоотдачи и температур охлаждающего агента по контуру: ![]()
Распределение расхода воздуха по поверхности оболочки представим по приближенной формуле:
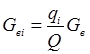 , (12)
, (12)
где 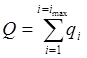 - подведенное к поверхности оболочки тепло.
- подведенное к поверхности оболочки тепло.
Интегральное уравнение теплоотдачи от газа к поверхности оболочки:
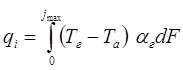
преобразуем, используя формулу трапеции:
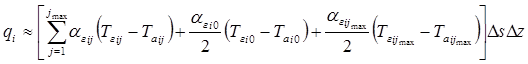 . (13)
. (13)
Таким образом, после решения задачи можно скорректировать распределение расхода воздуха, используя (11), (12), (13). При решении серии задач определяется оптимальный вариант распределения расхода охлаждающего воздуха с учетом требований теплоотдачи. Предложенный метод расчета позволяет отыскать необходимое распределение коэффициентов теплоотдачи, удовлетворяющее температурному полю рабочей лопатки газотурбинного двигателя.
Рецензенты:
Седельников Г.Д., д.т.н., профессор кафедры «Тепловые энергетические установки» ФГБОУ ВПО «Комсомольский-на-Амуре государственный технический университет», г.Комсомольск-на-Амуре.
Лейзерович Г.С., д.ф.-м.н., профессор кафедры «Механика и анализ конструкций и процессов» ФГБОУ ВПО «Комсомольский-на-Амуре государственный технический университет», г. Комсомольск-на-Амуре.



