В практике теплофизического эксперимента существуют два основных подхода к изучению теплопроводности бинарных органических растворов: аналитический и экспериментальный. В данной работе рассматривается комплексный (комбинированный) подход для прогнозирования теплофизических свойств (ТФС) различных растворов. Наиболее известные методы расчёта коэффициента теплопроводности были описаны в работе Рида Р. и др. [6]. Отличительной особенностью представленной статьи, являющейся новизной в экспериментальной теплофизике можно отметить, что метод кратковременных измерений в стадии иррегулярного теплового режима использован для исследования теплопроводности бинарных растворов органических жидкостей.
В настоящей работе представлен классический метод расчёта коэффициента теплопроводности для бинарных жидких растворов органических жидкостей. По результатам экспериментальных исследований предложена эмпирическая формула для каждой из групп по классификации Эвелла.
В качестве экспериментального метода выбран метод кратковременных измерений теплопроводности в стадии иррегулярного теплового режима [8], который позволяет уверенно различать теплопроводности жидкостей на уровне 0,1%.
Поскольку известно, что существуют значительные трудности в описании кинетических и термодинамических свойств даже простых жидких растворов, основанных на модельных представлениях о структуре, жидких растворов и характере теплового движения в этой среде, то в настоящее время при расчёте этих свойств, неопределённость – становится больше, чем погрешность теплофизического эксперимента. Принимая во внимание современные тенденции по совершенствованию методов расчёта, следует учитывать, что для проверки теории обязательна достоверность фактического материала. Так, проверка теории теплопроводности жидких растворов, особенно в области высоких температур должна непременно основываться на данных по молекулярной теплопроводности, как параметре непосредственно связанном со структурой жидкости, то использование для этих целей данных, которые отражают эффективную теплопроводность, может создавать неверные предпосылки по интерпретации результатов о согласовании литературных и экспериментальных данных. По мере совершенствования теории теплофизического эксперимента и методов её реализации будет повышаться важность всего выше сказанного.
Метод. В основе измерения теплопроводности лежит известная модельная задача [1]. Нить не ограниченной длины погружена и предельно малого радиуса 
(м) погружена в исследуемую среду. С единицы длины цилиндрической поверхности, параллельно оси z и проходящей через точку 
, выделяется в единицу времени постоянный тепловой поток 
. Температурное поле вокруг источника тепла с цилиндрическими изотермическими поверхностями будет двумерным. Но, в силу симметрии этого поля, достаточно рассмотреть изменение температуры вдоль одной координаты. Уравнение в цилиндрических координатах запишется тогда так:
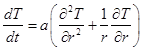(1)
где 
, 
- температуропроводность, м2/с; t - время, с; Т - температура, К.
Если тепло начинает выделяться в момент подачи импульса напряжения в 
, тогда линейный источник тепла и среда имеют нулевую температуру с учётом граничных и начальных условий можно записать:
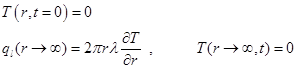
= const - постоянная линейная плотность теплового потока с нити, Вт/м; λ- теплопроводность среды, Вт/(м∙К).
Решение этой задачи известно [3]:
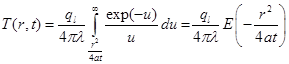(2)
где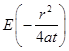 
- экспоненциальный интеграл. Разложив данный интеграл в ряд для малых значений параметра 
, или, соответственно для больших значений времени, получим[4]:
(3)
где С = 0,577 – постоянная Эйлера.
Реализация модельной задачи (1) выполнялась с помощью платиновой нити (резистивного элемента (РЭ)). РЭ имеет предельно малый радиус, чтобы можно было пренебречь его теплоёмкостью. Соответствующие количественные оценки были представлены в [7]. РЭ выполнял одновременно функции источника и приёмника тепла (термометра сопротивления).
Используя выражение (3), запишем изменение приращения температуры источника между моментами времени 
и 
:
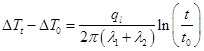(4)
Соотношение (4) позволяет определить теплопроводность исследуемого вещества 
по известной теплопроводности 
эталонного вещества и приращениям температуры источника в различные моменты времени.
Экспериментальные исследования базируются на использовании мостовой компенсационной схемы (рисунок 1), на которую с генератора подаются прямоугольные импульсы постоянного напряжения. Для индикации сигнала с моста используется осциллограф. В противоположные плечи моста включаются два зонда: измерительный с начальным сопротивлением 
и компенсационный с начальным сопротивлением 
. Зонды выполнены в виде тонкой платиновой нити.
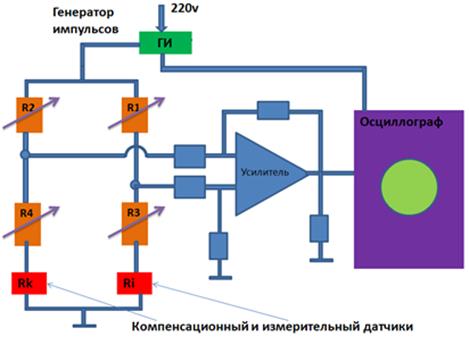
Рис. 1. Схема установки для проведения экспериментов
Принцип работы экспериментальной установки виден из рисунка 1. На мостовую схему подаётся прямоугольный импульс напряжения от генератора импульсов (ГИ). Сопротивления 
являются переменными и имеют минимальную абсолютную погрешность своих значений (порядка 0,05% на весь магазин переменных сопротивлений). Дифференциальный усилитель по напряжению необходим для усиления разности сигналов с плеч моста и так же для визуализации поступающего сигнала во время работы ГИ.
Пусть в исходный момент времени на мост подается напряжение U0 . Электрический сигнал с измерительных точек моста равен:
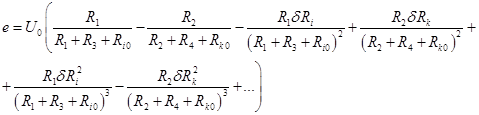(5)
Мост предварительно устанавливается на начальное сопротивление:
(6)
Поэтому, можно формулу (5) преобразовать в:
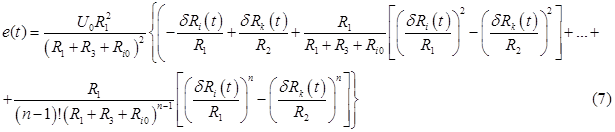
Следовательно, при условии
(8)
переменный сигнал скомпенсирован во времени (е(t)=0). Характерно, что компенсация осуществляется не только для первых членов разложения (5), но и для последующих. Последовательное осуществление баланса на начальные сопротивления (условие (6)) и компенсации переменной составляющей сигнала (условие (8)) представляет собой полный баланс мостовой схемы. Ячейка с измерительным зондом находится в термостате, температура которого меняется в ходе эксперимента. Компенсационный зонд помещается в сосуд с вазелиновым маслом и термостатируется при 0°С.
Непосредственная процедура измерения начинается с компенсации на эталонном веществе (толуол). Измерительный зонд при комнатной температуре 
вводят в контакт с толуолом, теплопроводность которого 
известна. При периодической подаче на схему прямоугольных импульсов напряжения, изменением сопротивлений R1 и R3 добиваются как баланса на начальные сопротивления, так и компенсации переменных сигналов. Частота подачи импульсов выбирается из условия, чтобы в паузе между ними происходила практически полная диссипация подводимой энергии. Когда е(t)=0, баланс проведен, при этом регистрируются значения R1ЭТ (Т0) и RiЭТ (Т0).
Затем, измерительный зонд вводится в контакт с исследуемым веществом. При температуре Т повторяется процедура полного баланса мостовой схемы и регистрируются значения 
и 
.
Соотношение для расчёта теплопроводности исследуемого вещества:
, (9)
где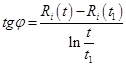 
.
Здесь λ – теплопроводность исследуемого раствора, Вт/(м∙К); α – коэффициент температурного сопротивления материала резистивного элемента датчика (α=0,00385 °С-1), °С-1; U0- подаваемое на мост напряжение с генератора импульсов, В; 
– длина нити датчика, м; 
- сопротивление измерительного датчика в момент времени , Ом; 
- сопротивление измерительного датчика в момент времени t1, Ом. Величина tgφ определялась для нескольких моментов времени: = 20мс, t1 = 25, 30, 35, 40, 50 мс. Максимальный нагрев РЭ в конце импульса не превышал 1°С. Основными источникам погрешностей являются: аппаратурные ошибки, связанные с измерением 
и методические погрешности, описанные в [7].
Преимущество такой методики заключается в том, что используемый для регистрации сигнал и осциллограф, используются в качестве индикатора сигнала, а измеряемыми параметрами при относительных измерениях являются сопротивления.
Используемые при измерениях датчики имели следующие характеристики: радиус нити 5мкм, длина 50мм, частота их подачи 1Гц. В паузе между импульсами происходила почти полная диссипация энергии, выделившаяся за время импульса.
Результаты исследования. Экспериментально изучены жидкие растворы в каждой группе по классификации Эвелла (см.таблицу). В таблице приведены экспериментально обобщённые константы жидкой смеси 
для каждой группы.
Значения константы для различных бинарных органических смесей внутри каждой группы
|
Класс |
Характеристика соединений |
Пример |
Константа |
|
2 |
Молекулы содержат активный водород и донор электронов (кислород, азот, фтор) |
Спирты, кислоты, фенолы, первичные и вторичные амины |
0,52 |
|
3 |
Молекулы имеют донор электронов, но в их отсутствует активный водород |
Эфиры, сложные эфиры, альдегиды, третичные амины |
0,48 |
|
4 |
Молекулы содержат активный водород и не содержат донора электронов |
Хлороформ, дихлорметан, дихлорэтан |
0,63 |
|
5 |
Молекулы без водородных связей |
Углеводороды |
0,38 |
Аддитивная схема расчёта теплопроводности представляет соотношение:
. (10)
Предлагается оценивать теплопроводность раствора соотношением:
, (11)
где 
- слагаемое, определяющее отклонение от линейности, 
- концентрация первой компоненты.
Величина определяется из эксперимента и достигает своего максимума при 
=0,5. Аналитически предлагается искать величину в виде:
. (12)
Параметр определялся в эксперименте.
, (13)
где – экспериментально регистрируемая величина.
Погрешность в экспериментальном определении величины не превышала 3%, разброс значений параметра – не более 5%.
Выводы. Полученные экспериментальные константы для полуэмпирического уравнения расчёта теплопроводности бинарных органических жидкостей в зависимости от концентрации компонент достаточно точно описывает экспериментальные данные, полученные с помощью импульсного иррегулярного теплового режима. Благодаря подобранным коэффициентам можно более точно прогнозировать теплофизические свойства бинарных жидких растворов по классификации Эвелла, в рамках конкретной группы.
Рецензенты:
Спирин Г.Г., д.т.н., профессор кафедры «Физика» ФГБОУ ВПО «Московский авиационный институт (национальный исследовательский университет)», г.Москва.
Гаряев А.Б., д.т.н., профессор, заведующий кафедрой «Тепломассообменные процессы и установки» ФГБОУ ВПО «Национальный исследовательский университет «МЭИ», г.Москва.