При производстве деталей и изделий из листовой электротехнической стали необходимо уделять особое внимание контролю магнитных характеристик материала, так как эти характеристики зависят от способа обработки. Помимо этого, необходимость такого контроля обусловлена получением готовой продукции (например электродвигателей) с заданными эксплуатационными параметрами. Промежуточный контроль магнитных характеристик (в частности B(H)-характеристики) стали и изделий на ее основе делает технологический процесс гибким и минимизирует процент брака готовых электротехнических изделий.
Известно устройство [3]. Данное устройство позволяет получить вебер-амперную и B(H)-характеристику характеристику участка детали из листовой электротехнической стали. Напряженность магнитного поля в образце определяется косвенным образом по формуле:
![]()
где I – ток, протекающей в намагничивающей обмотке; W – число витков намагничивающей катушки; ∆ – величина воздушного зазора, в который помещен образец.
Величина ∆ не постоянна, так как после входа в насыщение образца фактическое значение зазора возрастает за счет насыщения сердечника намагничивающей системы в районе контакта с образцом. Из-за этого возникает погрешность измерения напряженности магнитного поля на поверхности листа электротехнической стали. Для компенсации данной погрешности предлагается ввести канал измерения напряженности на поверхности испытуемой детали, представляющий собой линейку из n-датчиков Холла, расположенных на некоторых расстояниях x1...xn от листа электротехнической стали. Для определения числа датчиков и их местоположения необходимо построить модель топографии магнитного поля накладного датчика в окрестности испытуемого образца[2].
Для проведения измерений была построена модель накладного датчика. Моделирование выполнено при помощи программы ANSYS Maxwell. ANSYS Maxwell – высокопроизводительное интерактивное программное обеспечение, которое использует конечно-элементный анализ для решения электрических, магнитостатических задач, переходных задач и задач вихревых токов.
Трехмерная конечно-элементная модель представлена на рисунке 1, где 1 – испытуемый образец; 2 – магнитопровод; 3 – намагничивающие катушки. Отметим, что используя две плоскости симметрии, моделируется 1/4 датчика с целью уменьшения размерности модели и уменьшения времени расчета. Используя плоскость симметрии, моделируется 1/4 дифференциального магнитного моста с целью уменьшения размерности модели и времени расчета.
Измерения проводились вдоль оси Oz на отрезке [0,10] мм. Толщина листа стали 0,8 мм. Измерения проведены при различных значениях тока в намагничивающей обмотке. Результаты измерения представлены на рисунке 2.
Как видно из рисунка 2, зависимость напряженности магнитного H поля от расстояния до образца x носит практически линейный характер. Таким образом, для определения напряженности магнитного поля на поверхности испытуемого образца достаточно измерения напряженности p и H2 в двух точках пространства х1 и х2 и экстраполировании полученной зависимости в точку х=0 (рисунок 3).
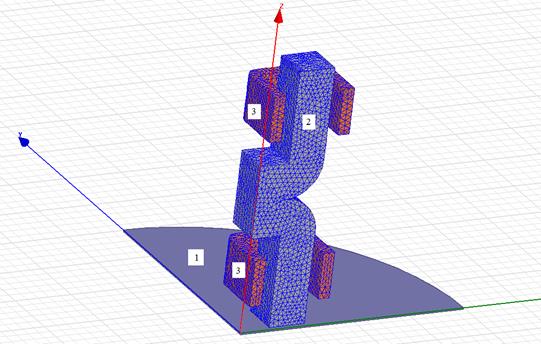
Рис. 1. Конечно-элементная модель накладного датчика
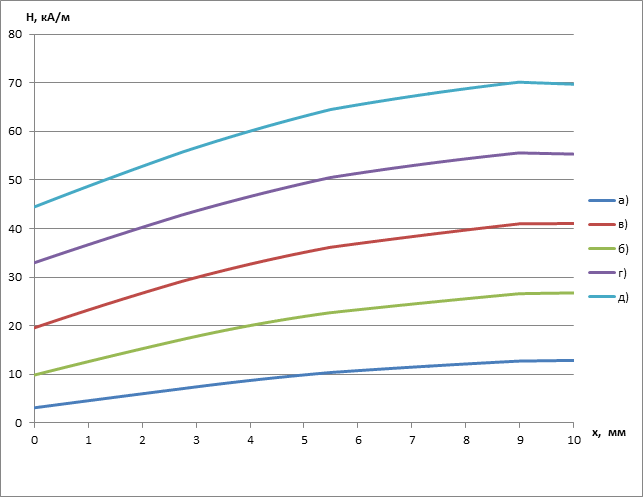
Рис.2. Результаты измерения при различном числе ампер-витков:
а) 200; б) 400; в) 600; г) 800; д) 1000.
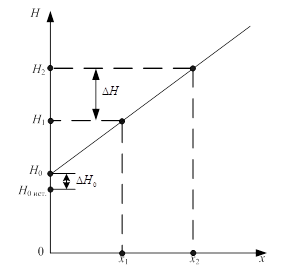
Рис.3. Определения напряженности МП на поверхности испытуемого образца
при использовании линейной экстраполяции
Расчет напряженности МП на поверхности ПМ производится по формуле [22]:
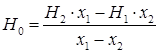 .
.
![]() ,
,
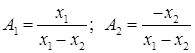
Таким образом, для нахождения значения напряженности магнитного поля на поверхности испытуемого образца достаточно знать значение напряженности магнитного поля в двух фиксированных точка на некотором удалении от поверхности.
Для оптимизации координат измерения напряженности магнитного поля воспользуемся методом крутого восхождения [20]. Метод крутого восхождения позволяет попасть из произвольной точки области исследования в область экстремума, поэтому выбор начальной точки не влияет на конечный результат. Задавшись произвольными координатами Хi0 начальной точки Оi, строим для области, прилегающей к ней, эмпирическую модель первого порядка:
![]()
Где: Вi –значения коэффициентов уравнения; Хi – факторы; Y – отклик.
Зададимся центром плана для всех факторов и интервалом варьирования исходя из априорной информации. Произведем кодирование факторов по формуле:
![]()
Для движения по методу крутого восхождения необходимо построить модель первого порядка для начальных координат. По полученному уравнению регрессии определяется градиент и производится движение поэтому градиенту до точки экстремума. Матрица планирования эксперимента 22 для нахождения уравнения регрессии первого порядка приведена в таблице 1. Обработка полученных результатов произведена посредством программного средства Statistica 6.0. Для анализа полученных результатов и проверки адекватности модели необходимо задаться числом повторных опытов m = 3. Зададимся погрешностью расчета значения погрешности 1%.
Таблица 1
Матрица планирования эксперимента
|
№ опыта |
Х1 |
х1, мм |
Х2 |
х2, мм |
Н0, кА/м |
δ, % |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
+ |
2.5 |
+ |
4.5 |
6.97 |
14.09 |
|
2 |
+ |
2.5 |
+ |
4.5 |
7.04 |
15.23 |
|
3 |
+ |
2.5 |
+ |
4.5 |
6.90 |
12.95 |
|
4 |
- |
1.5 |
+ |
4.5 |
6.47 |
6.00 |
|
5 |
- |
1.5 |
+ |
4.5 |
6.54 |
7.06 |
|
6 |
- |
1.5 |
+ |
4.5 |
6.41 |
4.94 |
|
7 |
+ |
2.5 |
- |
3.5 |
6.78 |
10.98 |
|
8 |
+ |
2.5 |
- |
3.5 |
6.85 |
12.09 |
|
9 |
+ |
2.5 |
- |
3.5 |
6.71 |
9.87 |
|
10 |
- |
1.5 |
- |
3.5 |
6.33 |
3.72 |
|
11 |
- |
1.5 |
- |
3.5 |
6.40 |
4.76 |
|
12 |
- |
1.5 |
- |
3.5 |
6.27 |
2.68 |
В результате получена адекватная модель со всеми значащими коэффициентами регрессии. Уравнение регрессии для кодированных значений уровней факторов имеет вид:
Y = 8,698+7,675 X1 + 2,699 X2.
Градиент имеет вид:
gradY = 7,675 i +2,699 j .
Произведем движение по градиенту к указанным координатам. Исходя из центра плана, интервала варьирования факторов и их граничных значений получаем шаг для первого фактора 0,2 мм, для второго фактора 0,4 мм. Движение по градиенту сведено в таблицу 2. Точка экстремума не найдена, но мы пришли к границе допустимых значений. Вид поверхности отклика и значение градиента указывает, что минимум погрешности будет при максимально близких к поверхности координатам точек измерения. Из физических ограничений размера датчика мы не можем приблизить точки измерения ближе чем х1=1 мм и х2=2 мм. Исследуем поверхность отклика в районе полученных координат.
Таблица 2
Движение по градиенту
|
№ шага |
х1, мм |
х2, мм |
δ, % |
|
1 шаг |
1.8 |
3.6 |
5.43 |
|
2 шаг |
1.6 |
3.2 |
3.06 |
|
3 шаг |
1.4 |
2.8 |
0.89 |
|
4 шаг |
1.2 |
2.4 |
0.47 |
|
5 шаг |
1 |
2 |
0.32 |
Матрица планирования эксперимента 22 для нахождения уравнения регрессии первого порядка приведена в таблице 3.
Таблица 3
Матрица планирования эксперимента
|
№ опыта |
Х1 |
х1, мм |
Х2 |
х2, мм |
Н0, кА/м |
δ, % |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
+ |
1.4 |
+ |
2.4 |
6.141 |
0.545 |
|
2 |
+ |
1.4 |
+ |
2.4 |
6.144 |
0.596 |
|
3 |
+ |
1.4 |
+ |
2.4 |
6.138 |
0.495 |
|
4 |
- |
0.6 |
+ |
2.4 |
6.122 |
0.234 |
|
5 |
- |
0.6 |
+ |
2.4 |
6.125 |
0.284 |
|
6 |
- |
0.6 |
+ |
2.4 |
6.119 |
0.184 |
|
7 |
+ |
1.4 |
- |
1.6 |
6.130 |
0.364 |
|
8 |
+ |
1.4 |
- |
1.6 |
6.133 |
0.414 |
|
9 |
+ |
1.4 |
- |
1.6 |
6.127 |
0.313 |
|
10 |
- |
0.6 |
- |
1.6 |
6.117 |
0.156 |
|
11 |
- |
0.6 |
- |
1.6 |
6.120 |
0.206 |
|
12 |
- |
0.6 |
- |
1.6 |
6.114 |
0.106 |
В результате получена адекватная модель со всеми значащими коэффициентами регрессии. Уравнение регрессии для некодированных значений уровней факторов имеет вид:
Y = -0,324+0,324 X1 +0,162 X2.
Изменение погрешности при движении показано на рисунке 5.
В результате оптимизации найдены координаты точек измерения, обеспечивающие минимальную погрешность при линейной экстраполяции значения напряженности магнитного поля на поверхности испытуемого образца. Т.к. оптимизация проводилась при среднем значении тока в намагничивающей обмотке, авторами проведена проверка погрешности экстарполяции при различных значениях тока в намагничивающей обмотке. Погрешность не превышает 1,1%.
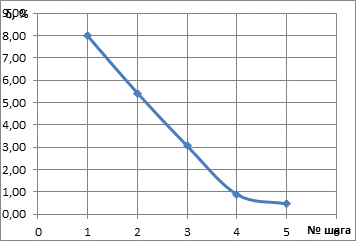
Рис. 5. Изменение погрешности при движении по градиенту
Рецензенты:
Горбатенко Н.И., д.т.н., профессор, И.О. первого проректора, ЮРГПУ(НПИ) им. М.И. Платова, г.Новочеркасск
Гречихин В.В., д.т.н., доцент, доцент кафедры ИИСТ, ЮРГПУ(НПИ) им. М.И. Платова, г.Новочеркасск.



