Анализ средств механизации погрузки горной массы, используемых в отечественной практике, показал, что значительная доля погрузочных машин приходится на машины непрерывного действия с парными нагребающими лапами [4,5]. Однако, используемый в них механизм исполнительного органа не всегда позволяет добиться на практике заявленной производительности. Это объясняется тем, что механизм исполнительного органа погрузочных машин не обеспечивает эффективный захват и передачу насыпного груза на конвейер, что приводит к накоплению материала в зоне перед приемным окном конвейера, а траектория движения передней кромки нагребающей лапы не охватывает полностью площадь приёмной плиты.
В процессе погрузки насыпного груза каждая из лап совершает одинаковые, непрерывно повторяющиеся движения: период внедрения лапы в штабель горной массы; период нагребания груза на плиту; период перемещения груза по плите до приёмного конвейера; период холостого хода лапы до начала следующего цикла.
Цель исследования
Производительность погрузочной машины непрерывного действия с парными нагребающими лапами зависит от объёма материала, захваченного за один цикл работы (один оборот кривошипа), который определяется площадью, заключённой внутри траектории движения передней кромки лапы [3].
Таким образом, повысить производительность погрузочной машины можно совершенствуя форму траектории, описываемую передней кромкой лапы, ее положение относительно приемной плиты, а также, увеличением площади, заключённой внутри траектории при заданных условиях захвата горной массы в процессе погрузки, что напрямую зависит от параметров кинематической схемы механизма исполнительного органа [1-3].
В современных шахтных погрузочных машинах непрерывного действия типа ПНБ механизмы нагребающих лап выполнены по следующим кинематическим схема: кривошипно-балансирной и кривошипно-шатунной с качающимся ползуном.
За базовую модель механизма принята кривошипно-балансирная схема механизма нагребающих лап погрузочной машины 2ПНБ-2, представленная на рисунке 1.
В представленной кинематической схеме приняты следующие условные обозначения:
r - радиус кривошина О1А; R - длина балансира О3В; l0 - длина шатуна АВ; l1 - длина рабочей части лапы АС; d1,d2 -координаты центра вращения балансира О3В; β - угол отклонения рабочей части лапы АС от прямолинейности. При этом, ширина приемной плиты В, расстояние от передней кромки плиты до приемного конвейера Н, а так же координаты центра вращения кривошипа О1 на приемной плите соответствуют параметрам погрузочной машины 2ПНБ-2.
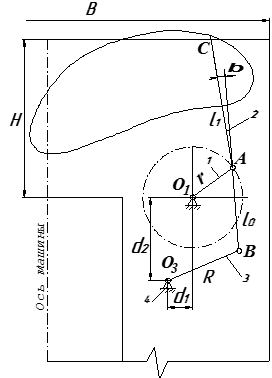
Рис. 1. Кинематическая схема кривошипно-балансирного механизма нагребающих лап:
1 – кривошип (ведущий диск); 2 – шатун (лапа нагребающая); 3 – балансир; 4 – стойка (приемная плита).
При этом, ширина приемной плиты В, расстояние от передней кромки плиты до приемного конвейера Н, а так же координаты центра вращения кривошипа О1 на приемной плите соответствуют параметрам погрузочной машины 2ПНБ-2.
Методы исследования
В качестве рациональных критериев оценки рассматриваемой кинематической схемы приняты форма траектории, описываемая передней кромкой лапы в габаритах приемной плиты, ее относительное расположение на приемной плите и площадь, заключенная внутри траектории.
Для обеспечения эффективного захвата насыпного груза траектория движения передней кромки лапы должна соответствовать следующим требованиям: вписываться в габариты приемной плиты погрузочной машины; не выходить за пределы бокового габарита приемной плиты с целью предотвращения возможного заклинивания лапы; выходить за переднюю кромку плиты на 20-50 мм для предварительного рыхления основания штабеля; пересекать осевую линию приемной плиты для увеличения площади, заключенной внутри траектории и для уменьшения «мертвых» зон, не охваченных траекторией; не заходить в зону приемного окна конвейера; иметь максимально возможную, заключенную в ней, площадь с учетом выше перечисленных требований.
Параметры кривошипно-балансирного механизма нагребающей лапы погрузочной машины типа 2ПНБ-2 позволяют получить траекторию не полностью отвечающую целевым функциям и поставленным ограничениям. Площадь, заключенная внутри траектории, составляет S=0,333м2 [1].
Для исследования влияния основных параметров кривошипно-балансирного механизма нагребающей лапы на качественные характеристики траектории, описываемой передней кромкой лапы, использовались аналитические и вычислительные методы, разработана математическая модель механизма.
Траектории движения характерных точек звеньев механизма определялись методами векторной алгебры, исследование поворотов производилось при помощи матриц поворотов [6]. Координаты точек вычислялись для цикла работы механизма, соответствующего углу поворота кривошипа от 0 до 360 градусов.
Реализованное в рамках вычисления программное обеспечение позволило определить параметры механизма, связывающие угол поворота ведущего звена O1A и координаты характерных точек звеньев механизма. Все необходимые вычисления выполнены автоматически для любой модификации механизма.
Для вычисления площади фигуры, описываемой передней кромкой лапы (точкой C) вычислялась площадь приближающего ее многоугольника, полученного при определении координат точки, для этого полученный многоугольник (невыпуклый) триангулировался [6].
Аналитическая база
Синтез кривошипно-балансирного механизма нагребающей лапы погрузочной машины, удовлетворяющий поставленным целевым функциям и ограничениям выполнен на основе составленной математической модели в программе MATLAB.
На рисунке 2 представлена схема кривошипно-балансирного механизма нагребающей лапы с условными обозначениями, принятыми в математической модели: r – радиус кривошина; R – длина балансира; l0 – длина шатуна АВ; l1 – длина рабочей части лапы АС; d1,d2 –координаты центра вращения балансира О3В; β - угол отклонения рабочей части лапы от прямолинейности; ![]() - угол поворота кривошипа;
- угол поворота кривошипа; ![]() - угол между векторами О3А и ВА.
- угол между векторами О3А и ВА.
В качестве переменных величин приняты: ![]() – радиус кривошипа;
– радиус кривошипа; ![]() ,
, ![]() – координаты центра вращения балансира
– координаты центра вращения балансира ![]() ;
; ![]() – угол отклонения рабочей части лапы
– угол отклонения рабочей части лапы ![]() от прямолинейности.
от прямолинейности.
Угол поворота кривошипа ![]() в момент времени
в момент времени ![]() равен
равен ![]() , где
, где ![]() - угловая скорость кривошипа.
- угловая скорость кривошипа.
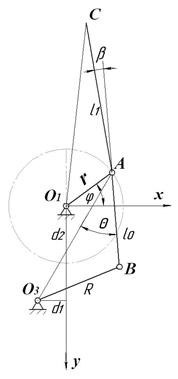
Рис. 2. Схема к математической модели кривошипно-балансирного механизма.
Координаты X и Y точки С, определяющие траекторию, описываемую передней кромкой лапы, определяются выражением:
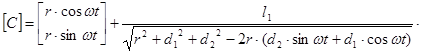
![]()
Координаты вычислялись для набора углов поворота кривошипа от 0 до 360 градусов с шагом 1 градус.
Результаты исследований
С учетом того, что площадь, заключенная в траектории, является функцией нескольких переменных, то последовательно рассмотрено влияние каждого из перечисленных параметров (r, d1, d2 и β), на форму, расположение и площадь траектории передней кромки лапы при сохранении остальных параметров постоянными.
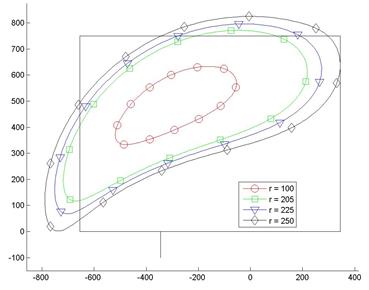
На рис.3 представлены траектории, описываемые передней кромкой лапы при значениях радиуса кривошипа r = 100, 205, 225 и 250 мм.
Изменение радиуса кривошипа в диапазоне 100 – 250 мм существенно влияет на величину площади, заключенную в траектории и в меньшей степени – на форму траектории и ее положение на приемной плите. При увеличении радиуса кривошипа r от 100 мм до 205 мм площадь траектории S возрастает от 0,08 м2 до 0,337 м2,т. е. в 4,21 раза.
y, мм
 x, мм
x, мм
Рис. 3. Траектории передней кромки лапы для значений радиуса кривошипа r =100, 205, 225, 250 мм.
При дальнейшем увеличении радиуса r от 205, 225 мм до 250 площадь траектории возрастает от 0,337; 0,407 до 0,504 м2, т.е. в 1,2 раза на каждом этапе, дальнейшее увеличение радиуса кривошипа свыше значения 250 мм не целесообразно, так как ведет к выходу траектории за пределы рабочей плиты, что не отвечает целевой функции механизма.
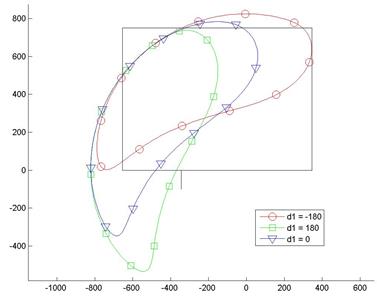
Координата d1 оказывает значительное влияние на положение траектории относительно приемной плиты (рисунок 4).
y, мм
 x, мм
x, мм
Рис. 4. Траектории передней кромки лапы для значений координаты d1 = 0,- 180, 180 мм.
При изменении координаты d1 от 0 до 180 мм наблюдается резкий поворот траектории в сторону приемного конвейера с заходом в зону приемного конвейера, что является недопустимым. Значение d1 = - 180 мм, определяет наилучшее положение траектории на приемной плите, при этом площадь, заключенная в траектории составляет 0,498 м2.
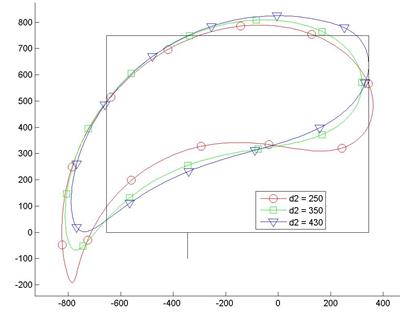
На рисунке 5 представлены траектории передней кромки лапы для различных значений координаты d2 при постоянных значениях r = 250 мм, d1 = -180 мм.
y, мм
 x, мм
x, мм
Рис. 5. Траектории передней кромки лапы для значений координаты d2 = 250, 350, 430 мм.
Центр вращения балансира О3 не может располагаться в зоне траектории кривошипной точки А, поэтому рассмотрен диапазон значений координаты d2 ≥ 250 мм. Так как при значениях d2 ≥ 430 мм механизм геометрически нереализуем, поэтому анализ влияния значений координаты d2 на площадь и расположение траектории ограничен диапазоном от 250 до 430 мм.
Анализ траекторий, представленных на рисунке 5 и соответствующих различным значениям d2 в диапазоне от 250 до 430 мм, показывает, что координата d2 оказывает значительное влияние на положение траектории на приемной плите и ее ориентацию относительно центра вращения кривошипа.
Так, при значении d2 = 250 мм наблюдается выход траектории за боковой габарит приемной плиты с одновременным значительным перекрытием зоны приемного конвейера, а при d2 = 430 мм траектория подходит вплотную к боковой грани плиты, не пересекая ее. Изменение координаты d2 от 250 до 430 мм увеличивает площадь внутри траектории от 0,481 до 0,504 м2.
Из вышесказанного был сделан вывод о целесообразности принятия параметра d2 = 430 мм.
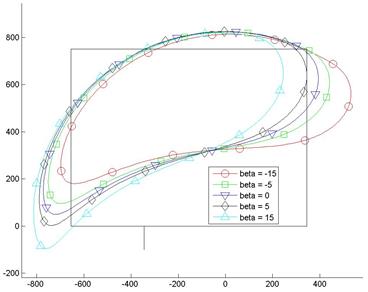
Влияние угла β исследовано в диапазоне значений от -150 до 150 при постоянных ранее определенных значениях r = 250 мм, d1 = -180 мм и d2 = 430 мм.
y, мм
 x, мм
x, мм
Рис. 6. Траектории передней кромки лапы для значений угла β = 00, ± 150.
Проведенные исследования показали, что угол β оказывает значительное влияние на положение траектории на приемной плите и ее ориентацию относительно центра вращения кривошипа. Так, при значении β = -150 наблюдается выход траектории за боковой габарит приемной плиты, а при β = 150 траектория значительно перекрывает зону приемного конвейера, при этом площадь, заключенная внутри траектории изменяется не значительно.
При переходе от значения β = 00 к оптимальному значению β = 50 площадь траектории изменяется менее, чем на 1% с 0,506 до 0,504 м2. При этом положение траектории в наибольшей степени соответствует принятым ограничениям, поэтому окончательно принят угол β = 50.
Заключение
На основании проведенного исследования установлены следующие рациональные параметры кривошипно-балансирного механизма нагребающих лап: r = 250 мм, d1 = - 180 мм, d2 = 430 мм, β = 50, обеспечивающие положение траектории на приемной плите полностью удовлетворяющее основным требованиям и принятым ограничениям и позволяющие получить площадь, заключенную внутри траектории S = 0,504 м2, что в 1,5 раза больше, чем для базовой модели механизма погрузочной машины 2ПНБ-2.
Полученные результаты и рекомендации могут быть использованы при исследовании и проектировании шахтных погрузочных машин непрерывного действия с парными нагребающими лапами.
Рецензенты:
Тарасов Ю.Д., д.т.н., профессор кафедры Горных транспортных машин, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Национальный минерально-сырьевой университет «Горный», г. Санкт-Петербург.
Козярук А.Е., д.т.н., профессор, заведующий кафедрой электротехники, электроэнергетики, электромеханики, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Национальный минерально-сырьевой университет «Горный», г. Санкт-Петербург.



