Вопросам безопасности людей в шахтах всегда уделялось особое внимание. Одной из важных задач, повышающих безопасность горнорабочих, является возможность отслеживать их местоположение внутри шахт. Спутниковые системы навигации, такие как ГЛОНАСС или GPS, невозможно использовать в закрытых пространствах. В таких случаях разрабатываются специальные системы локации [7, 11, 18].
Наиболее удобными для настройки и инсталляции являются технологии позиционирования, основанные на использовании беспроводных сетей датчиков [4]. Некоторые из таких систем основаны на анализе уровня принимаемого сигнала от стационарных точек доступа беспроводной сети (в основном такие системы используют WiFi, ZigBee или Bluetooth радио передатчики) [19]. Недостатком таких систем является низкая точность.
В некоторых случаях использую технологии, построенные на основе измерения расстояний с помощью ультразвука [12] или анализе распространения сигнала сквозь толщу породы [15].
Более точными являются системы, основанные на измерении времени распространения сигнала (ToF – Time of Flight). К таким радио технологиям можно отнести nanoLOC [5-6] и UWB [8, 9, 20, 21] (оба стандарта входят в IEEE 802.15.4a).
Чаще всего для определения местоположения объекта используют либо фильтр частиц [15], либо одну из модификаций фильтра Калмана [13], либо методы построения шаблонов карт слышимости (fingerprinting) [2, 10], либо их комбинации [14].
Как показано в [21], условия распространения электромагнитных волн в шахтах и тоннелях сильно отличаются от условий распространения на открытом пространстве и в зданиях. С одной стороны, тоннели позволяют "фокусировать" энергию волн, таким образом, сигнал может быть зарегистрирован на гораздо больших расстояниях по сравнению с открытым пространством. С другой стороны, даже частичная блокировка поперечного сечения каким-нибудь объектом приводит к резкому ухудшению условий распространения излучения.
Кроме этого, существует большая разница между шахтными штреками и автомобильными тоннелями. Как правило, стены автомобильных тоннелей делают достаточно ровными, а сами тоннели - прямыми, а стены шахт имеют большие неровности. Это приводит к дополнительному значительному затуханию сигнала в шахтах.
В данной статье рассматривается система локации RealTrac [1, 16, 17], основанная на беспроводной сети датчиков nanoLOC, использующих метод ToF для измерения расстояний от базовых станций до мобильного узла. Для измерения расстояний используются чипы компании Nanotron Technologies GmbH, работающие на частоте 2.4 ГГц. Типичная схема системы для определения местоположения на основе беспроводной сети датчиков изображена на рисунке 1.
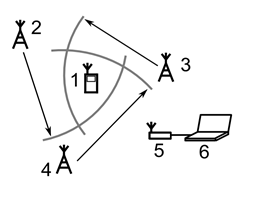
Рис. 1. Типичная схема системы локации на основе беспроводной сети датчиков. 1 – мобильное устройство; 2, 3, 4 – базовые станции; 5 – шлюз для передачи данных из беспроводной сети; 6 – сервер расчета локации
Система локации состоит из мобильного устройства (1), нескольких базовых станций (2, 3, 4), шлюза для передачи данных из беспроводной сети в проводной сегмент (5) и сервера расчета локации (6). В заданный интервал времени базовые станции проводят измерения расстояния и силы сигнала до мобильного объекта. Полученная информация отправляется на сервер, где производится расчет местоположения объекта.
Главным фактором, ухудшающим точность локации, является ошибка, связанная с непрямолинейным распространением сигнала. Датчик, находящийся на мобильном объекте может измерить не прямой сигнал от базовой станции, а отраженный от препятствия. В результате измеренное расстояние будет больше, чем истинное. Иногда эта ошибка может достигать нескольких десятков метров. Таким образом, окружности с радиусами измеренных расстояний не будут пересекаться в одной точке, а будут образовывать некоторую область локации (как показано на рисунке 1).
При использовании описанной системы для локации в шахтах необходимо учитывать ряд особенностей. В случае локации объекта на открытой поверхности (когда объект может двигаться в двумерной плоскости) для точного определения местоположения необходимо получить измерения минимум от трех базовых станций. Внутри шахт объект может двигаться только вдоль туннелей, в результате, для определения его местоположения достаточно двух, а иногда и одного измерения от базовой станции.
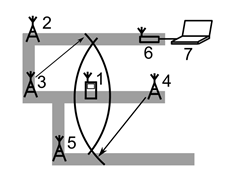
Радиосигнал с частотой 2.4 ГГц не может проходить через толщи породы. Поэтому, базовые станции необходимо размещать таким образом, чтобы всегда сохранялись условия прямой видимости между ними. Передача информации от мобильного объекта на сервер осуществляется по цепочке от одной базовой станции к другой. В результате, с точки зрения системы локации, шахта представляет собой граф туннелей, в вершинах которого находится базовые станции (рисунок 2). Станции располагаются таким образом, чтобы на каждом ребре было хотя бы по одной базовой станции.
Рис. 2. Схема системы локации для работы в шахте. 1 – мобильное устройство; 2, 3, 4, 5 – базовые станции; 6 – шлюз для передачи данных из беспроводной сети; 7 – сервер расчета локации.
В тоннелях измеренные расстояния между радиоузлами всегда выше истинных, поэтому местоположение объекта описывается отрезком (отрезками), сформированным(и) пересечениями отрезков, соответствующих измеренным расстояниям (см. рисунок 2).
Измерения расстояний проводятся периодически. За время между измерениями объект может переместиться на некоторое расстояние. Понятно, что зона вероятного местоположения объекта в этом случае должна быть расширена. Модель мобильного объекта подразумевает ограничение по его максимальной скорости. Поэтому, размер зоны зависит от периода времени между измерениями расстояний.
Таким образом, целью исследования является создание алгоритма, позволяющего оценивать локацию мобильных объектов в шахте, учитывающего ошибки измерений расстояний и возможное перемещение объектов в моменты между последовательными измерениями.
Одним из требований к алгоритму разрабатываемого решения является возможность одновременной локации большого количества устройств (более 2000 штук). Это накладывает ограничения на скорость работы алгоритма. При 5 секундном интервале между измерениями максимальное время расчета одной локации должно быть меньше 0.0025 секунды.
Математическая модель
В качестве математической модели шахты будем использовать граф. Ребрам графа соответствуют туннели шахты, вершинам – места разветвления туннелей и места расположения точек доступа. Все ребра графа считаем ориентированными, имеющими положительные веса, называемыми длинами ребер. Будем считать, что на ребрах графа находятся точки, для идентификации точки достаточно указать ребро и ее координату – неотрицательное число, не превосходящее длины ребра. Координата точки интерпретируется как расстояние от начала ребра до самой точки. Кроме того, на ребрах будем располагать отрезки, каждый отрезок можно определить его начальной и конечной точками, находящимися на ребре. Координата начальной точки отрезка не превосходит координату конечной точки. Отрезок состоит из точек ребра, находящимися между начальной и конечной точками отрезка. Естественным образом можно определить расстояния между точками, лежащими на одном ребре и между точками, лежащими на разных ребрах [3].
Мобильному объекту на графе соответствует некоторая точка, которую для определенности также будем называть объектом. Если в некоторый момент времени с некоторой погрешностью известно расстояние от заданной точки доступа до объекта, то вполне естественно в модели для указания местоположения объекта на графе использовать отрезки. При этом, отрезки графа состоят из точек, расстояние от которых до вершины графа, соответствующей точке доступа, находится в заданном интервале.
Таким образом, в каждый момент времени локация объекта характеризуется отрезками на графе, состоящих из точек возможного его расположения.
Если известна максимальная скорость объекта, то можно определить максимальное расстояние, на которое он может передвинуться за прошедшее после измерения время. Если начальное местоположение объекта было задано множеством отрезков, то возможное местоположение объекта после перемещения можно описать при помощи расширения всех отрезков на величину, равную максимально возможному пройденному расстоянию.
Простой алгоритм решения задачи расширения отрезков, который увеличивает длины всех отрезов и затем строит их пересечения, будет работать долго (в худшем случае, за время, пропорциональное кубу числа ребер графа). Поэтому был разработан специальный быстрый алгоритм расширения отрезков графа, описанный ниже.
Введем необходимые обозначения:
![]() – множество вершин графа;
– множество вершин графа;
![]() – множество вершин, инцидентных ребрам, на которых имеются исходные отрезки,
– множество вершин, инцидентных ребрам, на которых имеются исходные отрезки, ![]() ;
;
![]() – множество ребер графа;
– множество ребер графа;
![]() – множество ребер с исходными отрезками,
– множество ребер с исходными отрезками, ![]() ;
;
![]() – множество ребер, инцидентных вершине
– множество ребер, инцидентных вершине ![]() ,
, ![]() ;
;
![]() – расстояние между вершинами
– расстояние между вершинами ![]() и
и ![]() .
.
Расстояния между всеми парами вершин можно найти, например, с помощью алгоритма Флойда.
Пусть ![]() – ребро графа. Обозначим
– ребро графа. Обозначим ![]() – длину ребра
– длину ребра ![]() ,
, ![]() – упорядоченный список исходных отрезков ребра
– упорядоченный список исходных отрезков ребра ![]() .
.
Для ![]() и
и ![]() обозначим
обозначим ![]() – расстояние от вершины
– расстояние от вершины ![]() до ближайшего отрезка из списка отрезков
до ближайшего отрезка из списка отрезков ![]() инцидентного ей ребра
инцидентного ей ребра ![]() . Определим
. Определим ![]() как минимум среди расстояний от вершины
как минимум среди расстояний от вершины ![]() до отрезков на инцидентных ей ребрах:
до отрезков на инцидентных ей ребрах:
![]() .
.
На выходе описанного ниже алгоритма получим упорядоченные списки ![]() новых отрезков ребер
новых отрезков ребер ![]() , множество ребер
, множество ребер ![]() с расширенными и новыми отрезками, множество вершин
с расширенными и новыми отрезками, множество вершин ![]() , инцидентных ребрам с новыми отрезками. В ходе работы алгоритма увеличиваются длины отрезков на ребрах, на которых уже были отрезки, пересекающиеся новые отрезки объединяются, а также появляются отрезки на ребрах, на которых ранее отрезков не было.
, инцидентных ребрам с новыми отрезками. В ходе работы алгоритма увеличиваются длины отрезков на ребрах, на которых уже были отрезки, пересекающиеся новые отрезки объединяются, а также появляются отрезки на ребрах, на которых ранее отрезков не было.
Описываемый алгоритм состоит из трех этапов. На первой этапе определяются вершины, инцидентные ребрам с новыми отрезками. На втором этапа расширяются «старые» отрезки. На третьем этапа создаются отрезки на тех ребрах, на которых ранее отрезков не было.
Пусть ![]() – длина, на которую необходимо увеличить слева и справа все отрезки графа.
– длина, на которую необходимо увеличить слева и справа все отрезки графа.
Первый этап. Определение вершин, инцидентных ребрам с новыми отрезками
Первая часть алгоритма заключается в определении множества вершин графа, от которых необходимо отложить новые отрезки на ребрах графа.
1. Для каждой вершины ![]() вычислим
вычислим ![]() – длину, на которую будут отложены новые отрезки от вершины
– длину, на которую будут отложены новые отрезки от вершины ![]() .
.
2. Для каждой пары вершин ![]() ,
, ![]() определим
определим ![]() следующим образом:
следующим образом:
![]() .
.
3. Для каждой вершины ![]() вычислим
вычислим ![]() – длину, на которую должны быть отложены новые отрезки от вершины
– длину, на которую должны быть отложены новые отрезки от вершины ![]() :
:
![]() .
.
4. Определим множество вершин, инцидентных ребрам с новыми отрезками:
![]() .
.
Второй этап. Расширение «старых» отрезков
Рассмотрим вторую часть алгоритма, который увеличивает длину отрезков на ребрах множества ![]() и объединяет при необходимости пересекающиеся отрезки. Учитываются также отрезки, которые необходимо отложить от вершин, определенных первой частью алгоритма. В итоге, для ребер, на которых уже были отрезки, будут сформированы новые списки отрезков. Алгоритм эффективен по времени благодаря тому, что отрезки на каждом ребре перебираются в порядке удаленности их от начала ребра.
и объединяет при необходимости пересекающиеся отрезки. Учитываются также отрезки, которые необходимо отложить от вершин, определенных первой частью алгоритма. В итоге, для ребер, на которых уже были отрезки, будут сформированы новые списки отрезков. Алгоритм эффективен по времени благодаря тому, что отрезки на каждом ребре перебираются в порядке удаленности их от начала ребра.
Для каждого ребра ![]() выполним следующее. Пусть
выполним следующее. Пусть ![]() .
.
1. Если ![]() , то в начало списка
, то в начало списка ![]() отрезков ребра
отрезков ребра ![]() добавим отрезок
добавим отрезок ![]() , где
, где ![]() .
.
2. Если ![]() , то в начало списка
, то в начало списка ![]() отрезков ребра
отрезков ребра ![]() добавим отрезок
добавим отрезок ![]() , где
, где ![]() ,
, ![]() .
.
3. Положим ![]() , список
, список ![]() делаем пустым. Перебираем все отрезки
делаем пустым. Перебираем все отрезки ![]() списка
списка ![]() и для каждого отрезка выполним следующие шаги:
и для каждого отрезка выполним следующие шаги:
a. увеличим слева и справа длину отрезка![]() , получим отрезок
, получим отрезок ![]() , где
, где ![]() ,
, ![]() ;
;
b. если ![]() – первый отрезок списка
– первый отрезок списка ![]() , то присвоим
, то присвоим ![]() ;
;
c. если ![]() , то в конец списка
, то в конец списка ![]() добавим отрезок
добавим отрезок ![]() , затем присвоим
, затем присвоим ![]() ;
;
d. присвоим ![]() .
.
В конец списка ![]() добавляем отрезок
добавляем отрезок ![]() .
.
4. Положим ![]() .
.
Третий этап. Создание отрезков на ребрах, на которых не было отрезков
Для каждой вершины ![]() и для каждого ребра
и для каждого ребра ![]() выполним следующее. Пусть
выполним следующее. Пусть ![]() . Если список
. Если список ![]() пуст, то
пуст, то
1. Если ![]() , то в список
, то в список ![]() добавляем отрезок
добавляем отрезок ![]() .
.
2. Если ![]() , то
, то
a. если ![]() , то в список
, то в список ![]() добавляем отрезок
добавляем отрезок ![]() ;
;
b. если ![]() , то в список
, то в список ![]() добавляем отрезок
добавляем отрезок ![]() , где
, где ![]() ,
, ![]() .
.
3. Добавляем ребро ![]() в множество
в множество ![]() .
.
Время работы представленного алгоритма расширения отрезков равно ![]() , где
, где ![]() – максимальное число отрезков на одном ребре графа.
– максимальное число отрезков на одном ребре графа.
Множество полученных расширенных отрезков можно сократить, используя дополнительную информацию о местонахождении объекта. Пусть, например, после нового измерения сигнала известно, что объект удален от вершины ![]() на расстояние, заданное интервалом
на расстояние, заданное интервалом ![]() . Тогда можно убрать из рассмотрения те отрезки или части отрезков, точки которых удалены от вершины
. Тогда можно убрать из рассмотрения те отрезки или части отрезков, точки которых удалены от вершины ![]() на расстояние меньшее
на расстояние меньшее ![]() или большее
или большее ![]() .
.
Таким образом, перед каждым измерением необходимо запускать алгоритм расширения отрезков, который увеличивает область возможного нахождения объекта, а после измерения – отсекать «лишние» отрезки и, тем самым, сокращать область нахождения объекта.
Демонстрация работы алгоритма расширения отрезков
Рассмотрим пример работы алгоритма расширения отрезков. Пусть задан граф с семью вершинами (A, B, C, D, E, F, G) и восемью ребрами. Длины ребер: |AB| = 5, |AC| = 5, |BC| = 6, |BD| = 3, |CE| = 3, |DE| = 4, |DF| = 4, |EG| = 4 (рис. 3).
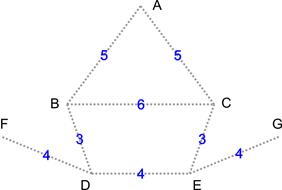
Рис. 3. Граф с 7 вершинами и 8 ребрами
Пусть в начальный момент времени на ребре BC находится отрезок BH, имеющий длину 2, и на ребре EG на расстоянии 2 от вершины E находится отрезок KL длиной 1 (рис. 4).
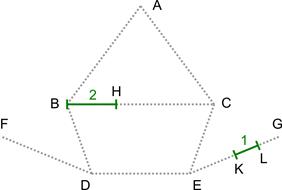
Рис. 4. Отрезки на ребрах, длина отрезка BH равна 2, длина отрезка KL равна 1, расстояние между точками E и K равно 2.
Пусть отрезки необходимо расширить на ![]() . На первом этапе алгоритма определяются числа
. На первом этапе алгоритма определяются числа ![]() (рис. 5).
(рис. 5).
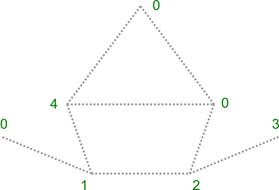
Рис. 5. Числа ![]()
На втором этапе алгоритма получаются новые отрезки (рисунок 6).
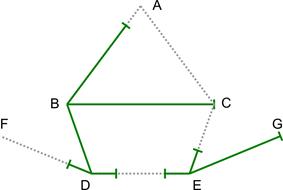
Рис. 6. На ребрах BC и EG расширились «старые» отрезки, на ребрах BA, DF, DE и EC были созданы «новые» отрезки
Далее, для оценки точности локации, рассчитанной с помощью описанного алгоритма, и оценки скорости работы был проведен следующий модельный эксперимент. Предполагалось, что объект равномерно двигался по графу туннелей, изображенному на рисунке.
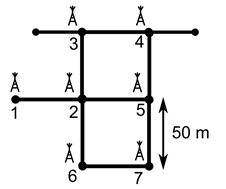
Рис. 7. Схема модельного эксперимента
Движения проходило от точки 1 до точки 7 по следующему маршруту 1-2-3-4-5-2-6-7. Длина ребра графа составила 50 метров, а скорость движения объекта – 3 м/с. Измерения расстояний до базовых станций происходили раз в 5 секунд. Считалось, что расстояния измерялись только до тех базовых станций, которые находились на одном ребре с мобильным объектом. В качестве измерений брались расстояния до базовых станций плюс ошибка (равномерно распределенная величина на интервале от 1 до 10 метров). С заданной вероятностью могло происходить событие «потеря сигнала», тогда считалось, что изменение расстояний было не успешным, и оно не принималось во внимание при расчете местоположения. За локацию объекта принималась точка на графе, ближайшая к центру масс точек, обозначающих середины отрезков, выдаваемых алгоритмом.
Оценка функции распределения ошибки локации для данного эксперимента представлена на рисунке 8.
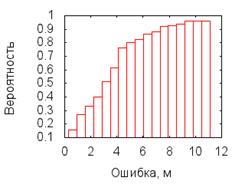
Рис. 8. Функция распределения ошибки локации для модельного эксперимента
Как видно, точность рассчитанной локации в 75% случаев составляет менее 5 метров. Максимальная ошибка локации может превышать максимальную ошибку в измерении расстояния (см. столбики ошибок выше 10 метров на гистограмме). Такая ситуация может наблюдаться, если в очередной момент расчета местоположения измерения признаются не успешными (эмуляция нестабильности радиосвязи), а зона локация, все равно, должна быть расширена вследствие неопределенности направления движения объекта с заранее известной максимальной скоростью.
Среднее время расчета локации на компьютере Samsung 900x с процессором Intel Core i5 для описанного эксперимента составило 0.8 мс. Максимальное время расчета составило 2 мс.
Заключение
Разработанный алгоритм локации внутри шахты позволяет определять локацию мобильных объектов с учетом ошибок измерений расстояний. Возможные точки положения мобильного объекта расположены на ребрах графа, описывающего структуру тоннелей. Характерный период между измерениями составляет несколько секунд. В качестве граничных условий задается максимальная скорость перемещения объекта.
Предложенный алгоритм обладает низкой вычислительной сложностью, и был применен для расчетов местоположения горнорабочих и горнодобывающей техники в режиме реального времени в системе локального позиционирования и передачи медиа данных RealTrac.
Исследования, описанные в статье, проводились в рамках деятельности МИП ООО "Наносети" и ЗАО "РТЛ-Сервис", а также поддерживались Петрозаводским государственным университетом (Программа стратегического развития ПетрГУ на 2012–2016 гг.), Министерством образования и науки РФ (гос. контракт 14.ВВВ.21.0162), Фондом СР МФП в НТС, Американским фондом гражданских исследований и развития (CRDF) и Министерством экономического развития Республики Карелии.
Рецензенты:
Колесников Г.Н., д.т.н., профессор, заведующий кафедрой механики Петрозаводского государственного университета, г. Петрозаводск.
Печников А.А., д.т.н., доцент, ведущий научный сотрудник лаборатории телекоммуникационных систем Института прикладных математических исследований Карельского научного центра Российской академии наук, г. Петрозаводск.



