Введение
Одним из важных требований при проектировании информационно-вычислительных систем (ИВС) является приемлемый уровень показателей их быстродействия и производительности. Чтобы спланировать затраты на оборудование при заданных параметрах конфигурации ИВС и показателях производительности, необходимо заранее рассчитывать прогнозируемые показатели оперативности их функционирования.
Для построения оценок оперативности функционирования информационно-вычислительных систем используется теория массового обслуживания(ТМО). В рамках ТМО рассматриваются стохастические процессы, для которых вводятся вероятностно-временные характеристики оперативности функционирования моделей систем массового обслуживания (СМО).
Существует несколько методов расчета вероятностно-временных характеристик СМО. Наиболее существенные практические результаты в публикациях связаны с применением итерационных методов для расчета немарковских систем, которые предложены Такахаши-Таками и получили развитие в [6]. Исходные немарковские распределения (длин интервалов между смежными заявками и длительности обслуживания) при названном подходе заменяются распределениями фазового типа. Указанный метод получил широкое распространение, поскольку, как показано Коксом в [8], с использованием распределений фазового типа может быть получена аппроксимация произвольных немарковских вероятностных распределений.
1. Расчет вероятностно-временных характеристик СМО с «разогревом»
Отметим, что актуальность исследований многоканальных немарковских СМО возросла в связи с массовой разработкой и внедрением распределенных и облачных систем различного масштаба – от локальных служб предприятия до глобальных услуг, доступных в сети Интернет.
При исследовании характеристик оперативности функционирования современных информационно-вычислительных систем для повышения точности моделирования в модели СМО зачастую требуется вводить дополнительные предположения, позволяющие учесть важные особенности организации вычислительного процесса. В некоторых работах, например в [3,9, 10], соответствующие модели СМО получили название систем с переменной скоростью обслуживания заявок или с «разогревом».
В работах [1,2,4] авторами настоящей статьи предложены расчетные схемы для вычисления стационарного распределения числа заявок в многоканальных немарковских СМО с аппроксимирующими распределениями фазового типа (гиперэкспоненциальным и обобщенным распределением Эрланга), неограниченной емкостью очереди и «разогревом».
Под «разогревом» понимается некоторая дополнительная работа, выполняемая системой, переходящей из свободного состояния в рабочий режим, но не характерная для обслуживания заявки, поступившей в уже работающую систему. Примером является облачная компьютерная система, работающая в режиме разделения времени, где при первом подключении после неактивности происходит кеширование данных в области оперативного доступа.
Программный комплекс
Отметим, что ранее на этапе получения результатов расчета моделей многоканальных немарковских СМО предоставляемые программисту возможности были ограничены как возможностями вычислительной техники, так и возможностями языков программирования. Основными языками программирования ранее были Алгол и Фортран, поэтому расчетные программы делались на них и оптимизировались под особенности конкретных рассчитываемых моделей.
Для расчета моделей СМО с «разогревом» потребовалось разработать отдельный программный комплекс, основанный на работах [1, 2, 4], так как существующие комплексы программ либо позволяют рассчитывать только упрощенные марковские системы с пуассоновским входящим потоком и экспоненциальным распределением длительности обслуживания, либо в силу ограничений времени написания оптимизированы под конкретные варианты немарковских систем, например, пакет [5].
Для преодоления указанных недостатков, при разработке одним из требований являлась максимальная применимость для расчета самого широкого класса моделей. С этой целью расчеты в программе проводятся в матричном виде, непосредственно по вычислительной итерационной схеме над абстрагированной СМО, а каждая конкретная модель СМО для расчета задается в отдельном классе, описывающем матрицы переходов над графом микросостояний данной модели и параметры, влияющие на расчет ее характеристик. За счет универсальности абстракции используемой объектной модели удалось обеспечить возможность расчета произвольных СМО, для которых применима используемая итерационная расчетная схема.
1.1 Общая характеристика программного комплекса
Программный комплекс обеспечивает расчет следующих характеристик:
-
стационарного распределения вероятностей микросостояний СМО в произвольный момент времени; на момент прихода очередной заявки в систему; на момент обслуживания очередной заявки;
-
стационарного распределения числа заявок в СМО.
Входные данные для программы - это свойства рассматриваемой модели. Обозначим через Sj множество всех микросостояний системы, когда на обслуживании находится ровно j заявок, а через σj - количество элементов в Sj. Определим матрицы переходов внутри системы из Sj:Aj[σj×σj+1] - в Sj (прибытие заявки), Bj[σj×σj-1] - в Sj-1 (полное завершение обслуживания заявки), Cj[σj×σj] - в Sj (конец промежуточной фазы обслуживания), Dj[σj×σj] - ухода из состояний яруса j (диагональная матрица).
Введём векторы-строки 
нахождения СМО в стоянии (j, i), j = 0,1,… Основная задача комплекса состоит в решении системы векторно-матричных уравнений баланса переходов между состояниями
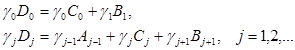
Решение ищется с учетом заданных граничных условий.
СМО может задаваться либо аналитически указанием матриц переходов между ними, либо диаграммой (графом) микросостояний системы, тогда матрицы можно построить по диаграмме переходов между микросостояниями. Помимо матриц переходов, задающих схему микросостояний системы, для работы программы необходимо задать n – число каналов системы, а также эмпирически полученные параметры распределений длительности интервалов входящего потока заявок, длительности «разогрева» и обслуживания.
2.2. Состав комплекса
Программы содержат следующие основные функции:
TakahashiTakami – функция расчета вероятностей числа заявок в СМО, работающая с входными параметрами модели.
CalculateProb – функция расчета вероятностей микросостояний СМО в произвольный момент времени, на момент прихода очередной заявки в систему, на момент обслуживания очередной заявки. Функция оперирует матрицами переходов модели и результатами расчетов функции TakahashiTakami.
CalculateMean – функция расчета среднего времени пребывания заявки в СМО и среднего времени ожидания заявки в СМО. Функция оперирует параметрами модели и результатами расчетов функции TakahashiTakami.
Вычисления средних значений базируются на рассчитанных вероятностях заявок в системе и основываются на законе Литтла сохранения очереди в СМО.
2. Подход к тестированию комплекса программ
Тестирование программных продуктов является на сегодняшний день отдельной областью знаний и даже отдельной профессией, в которой наработаны многочисленные и достаточно универсальные средства, технологии и инструменты. Лучшие практики тестирования основаны на постоянной проверке определенного набора тестовых сценариев в условиях постоянно развивающихся программных изменений.
Тем не менее для тестирования функциональной корректности определенного заданного комплекса программ имеет право на применение более простая техника тестирования, которая является не менее информативной и покрывает набор типовых тестовых сценариев.
В основу подхода к тестированию положен принцип взаимности, описанный в работе [5] – теоретический подбор исходных данных моделей таким образом, чтобы получаемые для них показатели давали одинаковые или близкие результаты. Отдельно проверяются граничные условия для входных параметров и особые случаи, если они имеют место в модели. Ниже показано, что распределение E2 является особым случаем для H2-аппроксимации.
3.1. Эквивалентные преобразования вероятностных распределений фазового типа
Несложно показать, что распределение Эрланга k-гo порядка Ek является частным случаем распределения k-гo порядка Кокса Сk. Нk-распределение может быть преобразовано к виду эквивалентного Сk-распределения. Эквивалентные преобразования используются для подбора параметров при решении задачи аппроксимации произвольного распределения распределениями фазового типа в случае, когда параметры аппроксимации выразимы аналитически одним видом распределения, но не выразимы другим. Решение задачи эквивалентного преобразования Нk-распределения к виду Сk сводится к решению системы разностных уравнений, оно приводится в работе [7].
Таким образом, между вероятностными распределениями фазового типа Сk, Нk и Ek существует взаимосвязь, позволяющая установить соотношение между ними. Заметим, однако, что прямое сопоставление Нk и Ek, невозможно, поскольку Ek-распределение не имеет эквивалентного гиперэкспоненциального распределения k-го порядка.
Схема выполнения взаимной проверки результатов с использованием различных типов распределений иллюстрируется на рисунке 1, где реализованные модели показаны по степени общности от базовой экспоненциальной слева до наиболее общей с использованием двухэтапного распределения Кокса (не рассматривается в нашей работе).
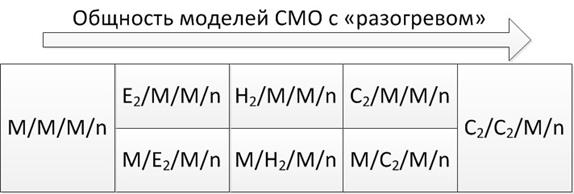
Рисунок 1. Схема взаимной проверки результатов вычислений
Модели, расположенные на рисунке левее, являются более частными случаями для моделей, расположенных на рисунке, соответственно, правее. Для совместной проверки вычислений, получаемых с распределениями Нk и Ek, сопоставляются наборы результатов в обоих классах при заранее подобранных значениях параметров, при которых характеристики сравниваемых моделей сходны.
3.2. Результаты расчета стационарных распределений вероятностей состояний системы
Каждый набор входных параметров рассчитывается независимо для распределений Нk и Ek, данные представлены в таблице 1.
Таблица 1. Входные параметры для моделей E2/M/M/3 и H2/M/M/3
|
Входные параметры модели E2/M/M/3 |
Входные параметры модели H2/M/M/3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
2,3 |
1,434 |
1,719 |
1,278 |
0,7 |
2,5 |
2,3 |
0,6 |
0,4 |
2,22 |
0,399 |
1,270 |
6,558 |
1,5 |
|
2,5 |
2,3 |
1,022 |
3,321 |
1,278 |
0,8 |
2,5 |
2,3 |
0,6 |
0,4 |
4,606 |
0,351 |
1,270 |
7,442 |
1,75 |
|
2,5 |
2,3 |
0,875 |
7,355 |
1,278 |
0,9 |
2,5 |
2,3 |
0,6 |
0,4 |
11,701 |
0,328 |
1,270 |
15,191 |
1,9 |
|
2,5 |
2,3 |
0,789 |
77,791 |
1,278 |
0,99 |
2,5 |
2,3 |
0,79 |
0,21 |
103,665 |
0,166 |
1,270 |
26,169 |
2,9 |
|
|
|
|
|
|
|
2,5 |
2,3 |
0,88 |
0,12 |
50,157 |
0,095 |
1,270 |
40,376 |
3,9 |
|
|
|
|
|
|
|
2,5 |
2,3 |
0,93 |
0,07 |
11,336 |
0,059 |
1,270 |
6,558 |
4,9 |
Сопоставление полученных стационарных распределений числа заявок в исследуемых моделях СМО E2/M/M/3 и H2/M/M/3 приведено на рисунке 2.
Результаты расчета стационарных распределений числа заявок в системах массового обслуживания E2/M/M/n и H2/M/M/n с «разогревом» для различных значений коэффициента вариации входящего потока заявок, показанные на рисунке 2, свидетельствуют о следующем. Семейство указанных распределений образует плавно изменяющийся набор распределений в пропорциональной зависимости от значений коэффициента вариации входящего потока заявок.
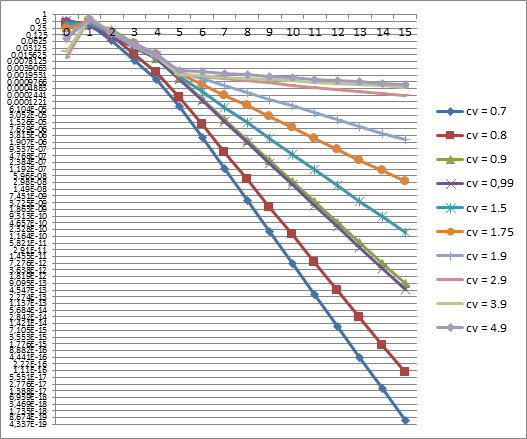
Рисунок 2. Стационарные распределения вероятностей состояний системE2/M/M/3 и H2/M/M/3
Модель многоканальной СМО E2/M/M/n с обобщенным распределением Эрланга входящего потока заявок покрывает совокупность значений коэффициента вариации в диапазоне от 0,7 до 0,99, модель многоканальной СМО H2/M/M/n покрывает совокупность значений коэффициента вариации в диапазоне от 1,5 до 4,9 соответственно. Пограничным значением коэффициента вариации является 1. Все это позволяет сделать вывод о согласованности результатов расчета стационарных распределений с помощью указанных моделей многоканальных СМО с «разогревом».
Еще один вариант проверки корректности моделей E2/M/M/n и H2/M/M/n с «разогревом» заключается в следующем: задаем для этих моделей при проведении численных расчетов очень большое значение интенсивности «разогрева», например, 
. Фактически это означает, что «разогрев» СМО происходит мгновенно, и соответствующие СМО можно сравнивать с многоканальной немарковской СМО GI/M/M/n с рекуррентным входящим потоком заявок и без «разогрева».
Заключение
Программный комплекс позволяет повысить точность получаемых вероятностно-временных характеристик за счет учета влияния «разогрева». Комплекс также применим для расчета вероятностно-временных характеристик СМО других классов. Выгодными отличиями комплекса являются возможности по интеграции для программистов и использование в расчетах многоканальных немарковских СМО.
Систематичность и полнота тестирования комплекса, положительные результаты тестирования позволяют считать программную реализацию корректной в рассмотренном диапазоне значений входных параметров. Согласованность полученных практических результатов на различных моделях говорит о надежности и верности теоретических основ выбранных алгоритмов.
Развитие комплекса предусматривает добавление возможностей: по работе с моделями, где аппроксимирующие распределения фазового типа имеют комплексно-сопряженные параметры; расчета временных характеристик (распределения времени ожидания заявки в очереди, распределения длин интервалов между заявками выходящего потока).
Рецензенты:
Арсеньев В.Н., д.т.н., профессор, профессор кафедры Бортовых информационно-измерительных комплексов, ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны Российской Федерации, г. Санкт-Петербург.
Ходаковский В.А., д.т.н., профессор, заведующий кафедрой «Математика и моделирование» ФГБОУ ВПО «Петербургский государственный университет путей сообщения Императора Александра I», г. Санкт-Петербург.