Важной частью всех значимых социально-экономических процессов, происходящих в настоящее время в мире, являются образование. Тенденции развития мировой экономики убедительно показывают, что единственным путем «интенсивного» развития России является формирование экономики, основанной на знаниях. В рамках присоединения к Болонскому процессу идет постепенный переход на двухуровневую систему подготовки бакалавр-магистр, глубокой модернизации подверглись программы обучения. В свою очередь, это потребовало изменения существующих методов оценки качества обучения студентов.

Исследованием компетентностного подхода в целом, и компетенции в частности, занимались многие отечественные и зарубежные ученные. Предложено множество содержательных идей и подходов, касающихся терминологии, структуры и моделей компетенций, однако проблема оценки сформированности компетенций, формируемых в процессе образовательной деятельности в ВУЗе, до сих пор не имеет общепризнанного решения ни у нас в стране, ни за рубежом. Основная проблема здесь кроется в том, что компетенция, по своей сути, личностное качество (свойство) человека [4], непосредственно влияющая на ту или иную деятельность, напрямую не может быть диагностирована. Мы видим и можем оценить только последствия, итоговый результат деятельности.

Сформулируем следующий вопрос: если возможна количественная оценка результатов практической деятельности, возможна ли оценка скрытого влияющего фактора? Существует несколько различных научных направлений, изучающее взаимодействие факторов и видимых последствий. На наш взгляд наибольшего внимания заслуживает латентно-структурный анализ, и, в частности, IRT-теория.

Основы IRT

Основные логические и математические основания латентно-структурного анализа были изложены в 60 гг. XX века в работах американского социолога П. Лазарсфельда, и подытожены в монографии, подготовленной П. Лазарсфельдом и Н. Генри [3]. Параллельно с Лазарсфельдом, работы в данном направлении проводил датский математик Георг Раш. Раш предложил математическую модель, которая в наше время известна как однопараметрическая модель Раша и ввел две меры: «логит уровня знаний» и «логит уровня трудности задания». Первую он определил как натуральный логарифм отношения доли правильных ответов испытуемого, на все предложенные задания, к доле неправильных ответов, а вторую – как натуральный логарифм другого отношения – доли неправильных ответов на задания к доле правильных ответов на тоже задание, по множеству испытуемых. Аналогичные исследования проводили так же A.Birnbaum, и F.M.Lord.

Дальнейшее развитие данного направления привело к появлению Item Response Theory. К настоящему времени, за рубежом появились десятки тысяч научных исследований по IRT, возникла эффективная практика применения теории, на её основе создаются адаптивные обучающие и контролирующие системы многих университетов и стран. Разработано большое количество различных математических моделей, охватывающие практически все возможные ситуации, однако, в России IRT практически не известна: основные публикации на русском языке посвящены только моделям Раша и Бирнбаума, частным случаям IRT.

В России название IRT переводили такими словами, как «теория латентных черт», «теория характеристических кривых заданий», «теория моделирования и параметризации педагогических тестов», «современная» теория тестов и т.д. Столь заметные различия в переводах одного только названия IRT уже само по себе являются свидетельством неблагополучия в понимании её сути. Не лучшим образом обстоит дело с переводом на русский язык исходных понятий и положений IRT [1]. Поэтому, в рамках данной статьи мы будем преимущественно пользоваться английскими терминами.

Основной предмет применения математических моделей IRT – оценка вероятности правильного ответа испытуемых на задания различной трудности. В IRT анализируются не суммы баллов испытуемого, а баллы, полученные по каждому заданию. Исходные аксиомы измерений сводятся к тому, что интересующее свойство личности:

• существует, в латентном состоянии;
• оно устойчиво;
• имеется у данных испытуемых, в каких-то количествах;
• измеряемо, с некоторой погрешностью.

IRT позволяет решить три ключевые задачи педагогического измерения:

• найти параметры заданий;
• найти параметры испытуемых;
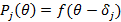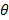• подобрать функцию , где – значение исследуемой латентной переменной, – уровень трудности j-го задания.

Обобщенно IRT модель может быть записана в следующем виде:

где – оценка для j-го человека по i-ому дихотомическому заданию (т.е. ответы могут быть только 0 или 1)

– параметр, описывающий латентную характеристику j-го человека (как правило, это способность или уровень достижений, связанный с выполняемыми заданиями)

­– характеристика i-го пункта теста (задания).

Исторически первой и основной математической моделью IRT является однопараметрическая модель (1PL). Математически она, практически, идентична модели Раша, однако, как отметил в своей работе [7] D.L.McArthur, они несколько различаются концептуально. Модель может быть записана в следующем виде:

Пример графика логистической функции при представлен на рис. 1. На графике хорошо видно монотонно возрастающее отношение между уровнем подготовленности человека и вероятностью правильного ответа на задание. В англоязычной литературе подобный график принято называть item characteristic curve (ICC).

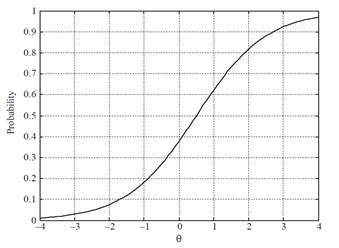
Рис. 1. Характеристическая кривая задания при

Наклон характеристических кривых в области вероятности =0,5 определяет дифференцирующую способность задания. В случае, когда исследуемый набор заданий включает в себя задания с различной дифференцирующей способностью, однопараметрическая модель становится некорректной. А.Бирнбаумом предложена двухпараметрическая модель (2PL), учитывающая различную дифференцирующую способность задания:

где – дифференцирующая способность задания.

Известна также и трехпараметрическая модель (3PL), в которой третий параметр учитывает способность студента угадать ответ на задание (параметр угадывания).

где – параметр угадывания.

Представленные выше модели просты и понятны, однако, обладают одним общим свойством – они могут применятся только к дихотомическим заданиям. Это резко ограничивает их применяемость – для оценки какого-либо свойства необходимо создавать набор заданий, ответами на которые могут быть только да или нет (истина или ложь и т.п.). Гораздо чаще встречаются задания, в которых возможны промежуточные варианты ответов, либо же вообще вариантов нет, вопрос является открытым, и ответ оценивается в какой-либо шкале (в отечественной педагогической практике часто используется пятибалльная). Примером модели, учитывающую градацию правильных ответов, является Partial Credit Model (PCM):

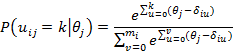
где

– оценка по i-ому заданию,

– максимальная оценка i-го задания,

– threshold (пороговой) параметр, определяет сложность достижения каждого пункта шкалы.

Для упрощения расчетов принимается, что

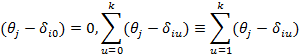
Пример ICC графика приведен на рис. 2.

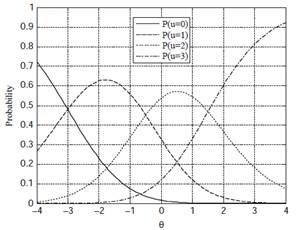
Рис. 2. График ICC для задания с threshold-параметрами -3, -0.5, 0, 1.5

Использование IRT

Корректность математической модели IRT – многоаспектное понятие, включающее в себя вопросы формирования наборов первичных баллов, применение модели и последующей интерпретации результатов. При этом отметим, что интерпретация результатов несколько отличается от технологий, принятых, например, в таких науках, как физика, химия и т.п. В них полученные эмпирические данные описываются с помощь какой-либо теории. Если теоритические зависимости не соответствуют полученным практическим результатам, делается вывод, что теория не верна или до конца не доработана. В IRT теории применим кардинально иной подход (пример другой философии измерения – model based measurement) – не модель должна соответствовать эмпирическим данным, а данные должны соответствовать модели. Об этом можно спорить, но в соответствии с философией IRT для оценки латентного фактора стоит использовать только те задания, которые отвечают данной модели измерения. Все остальные задания должны быть изменены или отбракованы [2]. Для того, чтобы проверить, соответствуют ли эмпирические данные той или иной модели, разработаны разнообразные статистики. Наибольшее распространение получили так называемые fit статистики: Outfit и Infit [5].

Цели fit статистики – определить части исходных данных, которые не отвечают модели. Причем, не удовлетворяющие статистикам части не отвергаются автоматически – требуется дополнительная проверка, почему они не соответствуют модели, и можно ли их каким-либо образом модифицировать. И Outfit и Infit статистики существуют в двух вариантах: обычный (MEANSQ, математическое ожидание 1) и стандартизированной (ZSTD, математическое ожидание 0).

Пусть остатки вычисляется по формуле:

где – ответ респондента n на задание i,

– ожидаемый ответ согласно IRT модели.

Стандартизованные остатки:

Тогда OUTFIT MEANSQ рассчитывается по формуле:

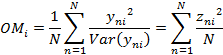
где – количество респондентов.

OUTFIT ZSTD:

где – MSWD (Mean square weighted deviation), взвешенное среднеквадратическое отклонение.

INFIT MEANSQ:

INFIT ZSTD:

Возможная интерпретация данных статистик согласно John M. Linacre [6] приведена в таблицах 1 и 2.

Таблица 1

MEANSQ OUTFIT и INFIT

Таблица 2

ZSTD OUTFIT и INFIT

Вопрос, какие же значения статистки являются достаточными для практического применения, однозначного ответа не имеет. Согласно [6] считается, что следует использовать значения MEANSQ в диапазоне 0,4 – 1,6, а ZSTD: -2,5 – +2,5.

Таким образом, предлагаемая методика применения IRT для оценки компетенций выглядит следующим образом:

• определяются индикаторные переменные (задания), которые являются видимым следствием проявления латентной переменной (компетенции);
• формируется матрица оценок индикаторных переменных;
• выбирается исследуемая IRT модель;
• проводится оценка параметров модели, определяются значения описательных статистик;
• на основе исследования значений статистик делается вывод о применимости модели, определяются слабые места, принимается решение о необходимости модификации тех или иных заданий;
• если значения статистик подтверждают, что данные соответствуют модели, строится шкала оценок компетенции в логитах. Если нет, то может быть исследована другая модель, либо проведена модификация набора индикаторных переменных.

Пример

Исследуем с помощью изложенной выше методики оценку компетенций ПК-10 (способен применять к решению прикладных задач базовые алгоритмы обработки информации, выполнять оценку сложности алгоритмов, программировать и тестировать программы) направления «Прикладная информатика в экономике». Пусть определен список предметов, которые формируют данную компетенцию: математика, основы алгоритмизации, информатика и программирование, разработка и стандартизация программных средств, высокоуровневые методы информатики и программирования, междисциплинарный экзамен по специальности. Исходными баллами будут являются экзаменационные оценки. Экзаменационные оценки выставляются в пятибалльной шкале, однако оценка 1 не используется практически никогда, а оценка 2, хоть и выставляется, однако у студента всегда есть возможность пересдать, в противном случае студент подлежит отчислению. Исследование будет касаться только успевающих студентов, так что шкала для PCM будет иметь три категории {cat1, cat2, cat3}, соответствующим оценкам {3,4,5}. Выборка студентов специальности «Прикладная информатика в экономике» за 7 лет составила 139 человек. Для оценки параметров IRT модели был разработан специальный программный комплекс. Исходные данные берутся из информационной системы ВУЗа. Оценки параметров модели и статистики приведены в таблицах 3 и 4.

Таблица 3

Сложность заданий согласно модели PCM с тремя категориями

Таблица 4

Значения статистик заданий

Анализируя результат, представленный в таблице 4, можно сделать вывод, что в целом задания удовлетворяют модели PCM и их (возможно, с некоторыми модификациями) можно использовать для оценки компетенции. Некоторые задания проявляют слабость в первой категории, что может свидетельствовать о том, что тройки «натягиваются» студентам. Этот вывод подтверждает, и оценка сложности заданий, представленных в таблице 4. Если для того, чтобы с вероятностью 50% студент получил оценку 5, он должен обладать уровнем освоения компетенции в диапазоне 1-2 логита, а для четверки -0,5 – +0,5, то для получения тройки по некоторым предметам вполне хватит уровня освоения -5 – -4. Особняком стоит предмет «Основы алгоритмизации» - для того, чтобы получить по нему пятерку, вполне хватит уровня освоения 0,2. Более того, сложность получения четверки меньше, чем сложность получения тройки. Threshold (пороговые) значения представлены в таблице 5.

Таблица 5

Threshold значения категорий

Наиболее сложным для получения оценки «отлично» на экзамене является предмет «разработка и стандартизация», а легким – «основы алгоритмизации». Четверку получит легче всего опять же на «основы алгоритмизации», при этом отметим, что грань между тройкой и четверкой крайне мала. Тоже самое относится и к математике. Вероятно, необходимо модифицировать экзаменационное задание таким образом, чтобы они лучше идентифицировали «слабых» и «средних» студентов, особенно это касается «основ алгоритмизации». Тройку легче всего получить на «информатике и программировании».

Оценки сформированности компетенции для исследуемой выборки студентов (в логитах) представлены в таблице 6. Сумма балов и максимальное количество баллов рассчитывались по приведенной шкале {1,2,3}.

Таблица 6

Оценка сформированности компетенции

Однако подобная методика измерения в логитах непривычна для отечественных педагогических работников. Но, благодаря тому, что измерения параметров IRT модели является линейными, полученные логиты могут быть легко преобразованы, например, в стабильную рейтинговую шкалу с помощью линейного преобразования. В процессе преобразования можно выделить два момента. Первый — это умножение всех значений параметра на один и тот же шкалирующий множитель и последующее округление для перевода результатов в область целых чисел. Второй – перенос всех значений параметра на множество положительных чисел путем прибавления некоторой константы, позволяющей избавиться от всех отрицательных оценок параметра.

Несомненным плюсом применения IRT моделей является возможность получать одновременно с оценками компетенций студентов обоснованные статистические оценки заданий, что может служить основой для улучшения образовательных программ ВУЗа. Оценка уровня подготовленности испытуемых не зависит от набора заданий, а неполнота данных (пропуск некоторых комбинаций «испытуемый - задание») не является критичной. Однако нельзя не отметить, что исследуемые задания должны быть гомогенными («одномерными»), т.е. формирующими и оценивающим только одну компетенцию, а некоторые экзаменационные задания лишь с натяжкой можно считать таковыми. Есть два основных пути увеличения объективности, получаемых согласно предложенной методики, результатов, а также расширение сферы применяемости: использования в качестве «сырых» баллов не экзаменационных оценок, а оценок, получаемых при промежуточной аттестации за выполнение различных заданий. Этот путь требует пересмотра и значительного расширения банка контрольных заданий по каждому предмету – каждое отдельно взятое задание должно диагностировать только одну компетенцию. Так же это должно найти отражение в информационной системе ВУЗа – учет и хранение этих оценок. Второй путь – это использование моделей, представленных в «многомерном» расширении IRT – Multidimensional Item Response Theory (MIRT), однако это увеличивает сложность расчетов.

Рецензенты:

Пархомов В.А., д.ф-м.н., профессор кафедры Информатики и Кибернетики ФГБОУ ВПО «Байкальский государственный университет экономики и права», г. Иркутск.

Боровский А.В., д.т.н., профессор кафедры Информатики и Кибернетики ФГБОУ ВПО «Байкальский государственный университет экономики и права», г. Иркутск.