Введение
Повышение эффективности изучения учебно-справочных материалов (таких, как ресурсы wiki, словари BaseGroup, а также глоссариев различных программных пакетов, например Statistica, Mathcad, Matlab и др.) возможно за счет определения порядка изучения, при котором полученных ранее знаний будет достаточно для освоения каждого следующего фрагмента контента. Для этого нужна структура предметной области, соответствующая имеющемуся контенту. Примерами моделей таких структур являются классификаторы УДК, ГРНТИ и т.п. Однако они охватывают слишком широкую предметную область, за счет чего сложны для поиска отдельного раздела. Другим недостатком является недостаточная детализация таких классификаторов – они заканчиваются практически на том уровне, с которого начинаются классификации понятий предметных областей прикладных задач. Справочные информационные ресурсы, как правило, упорядочены по алфавиту. Построить семантическую модель на уровне прикладной задачи вручную, не имея достаточных знаний в соответствующей предметной области, весьма затруднительно.
Для выявления структуры учебно-справочных материалов предлагается сначала разделить их по темам, т.е. сформировать кластеры, содержащие учебный контент сходной тематики. Затем определяются траектории освоения материала, определяющие последовательность изучения на различных иерархических уровнях. Таким образом, для формирования структуры учебно-справочных материалов необходимо выполнить следующие этапы.
-
Индексация всего множества фрагментов учебного контента.
-
Кластеризация фрагментов учебного контента.
-
Упорядочение фрагментов контента внутри кластеров – формирование траекторий освоения материалов нижнего уровня.
-
Упорядочение полученных кластеров – формирование траектории освоения материалов верхнего уровня.
На первом этапе, с целью автоматизации процесса структурирования учебно-справочных материалов, выбранные фрагменты контента индексируются на основе тезауруса запросов обучающихся одним из способов, рассмотренных в [1]. Разработана программа, позволяющая автоматически формировать тезаурус на основе указания одной наиболее общей (родительской) темы [2].
Для примера выберем фрагменты электронного учебного контента в области информационных систем и технологий по нескольким темам и обозначим их ![]() ,
, ![]() (в выбранном примере
(в выбранном примере ![]() ): «Системы управления базами данных» (C1– СУБД), «Базы данных» (C2– БД), «Модель данных» (C3– МД), «Предметная область» (C4– ПО), «Экспертные системы» (C5– ЭС), «Корпоративные информационные системы» (C6– КИС), «Информационные системы» (C7– ИС), «Информационные технологии» (C8– ИТ).
): «Системы управления базами данных» (C1– СУБД), «Базы данных» (C2– БД), «Модель данных» (C3– МД), «Предметная область» (C4– ПО), «Экспертные системы» (C5– ЭС), «Корпоративные информационные системы» (C6– КИС), «Информационные системы» (C7– ИС), «Информационные технологии» (C8– ИТ).
Пусть тезаурус содержит термины, соответствующие названиям одноименных статей, и расширяется двумя дополнительными терминами: «Реляционная модель» и «MySQL», которые близки по тематике к выбранным темам (ссылки на них несколько раз встречаются в рассматриваемых фрагментах контента). Таким образом, формируется базис B, содержащий элементы ![]() ,
, ![]() , являющийся основой для определения индексов фрагментов учебного контента.
, являющийся основой для определения индексов фрагментов учебного контента.
Для индексации контента строится матрица I (Index), строки которой являются индексами фрагментов контента, т.е. в строках содержатся коэффициенты разложения по базисным векторам для соответствующих фрагментов контента. Вхождение элементов базиса определяется, в данном случае, по наличию ссылок из фрагмента контента на каждый из элементов базиса: если ссылка есть – 1, если нет – 0 (таблица 1), т.е. элемент матрицы ![]() , если фрагмент i содержит ссылки на j-й элемент базиса, и 0 – в противном случае.
, если фрагмент i содержит ссылки на j-й элемент базиса, и 0 – в противном случае.
Таблица 1. Матрица I бинарных индексов фрагментов контента
|
|
B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
B7 |
B8 |
B9 |
B10 |
|
C1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
C2 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
C3 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
C4 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
C5 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
C6 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
C7 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
C8 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
На втором этапе для решения задачи кластеризации воспользуемся бинарным индексом фрагментов контента. При кластеризации алгоритмом k-means, в зависимости от выбора количества кластеров q (с использованием пакета DeduktorBasegroup), получены следующие результаты:
q=2: {С1, С2, С3}, {С4, С5, С6, С7, С8}; (1)
q=3: {С1, С2, С3}, {С4, С5}, {С6, С7, С8}. (2)
Обычно кластеризация рассматривается как метод обучения без учителя, который группирует объекты на основе только той информации, которая представлена в самих множествах объектов и не использует дополнительную информацию. В реальных задачах зачастую возникают дополнительные ограничения и условия, для учета которых необходима дополнительная информация об объектах и их связях или о размерах кластеров, которые желательно получить. Использование такой информации может существенно облегчить обработку результатов кластеризации (т.к. полученные результаты уже будут учитывать ограничения задачи). Однако традиционные алгоритмы, например k-means, не предоставляют механизма учета такой информации.
Альтернативой применения алгоритма k-means является кластеризация с помощью построения дендрограмм [1]. Объединяя «снизу вверх» уровни дендрограммы до тех пор, пока количество элементов в кластерах не превышает заданные ограничения, можно получить «оглавление» выбранной предметной области, т.е. распределение фрагментов учебных материалов по темам.
Исходными данными для задачи кластеризации с ограничениями на размер кластеров является количество объектов в каждом кластере. При этом, учитывая, что общее количество объектов известно, можно рассчитать минимальное количество кластеров для такого разбиения. В отдельных задачах количество кластеров может быть задано.
Пусть в рассматриваемом примере ограничение на размер кластера составляет 3 элемента, т.е. в каждый из кластеров должно входить не более трех элементов.
Тогда из представленных результатов кластеризации ограничению задачи удовлетворяет только разбиение (2), т.к. в разбиении (1) присутствует кластер с пятью элементами.
На третьем этапе формируются траектории освоения материалов нижнего уровня.
Траектории нижнего уровня, представляющие собой последовательность объектов, входящих в отдельные кластеры, могут быть построены:
- экспертным путем, на основе определения парных дидактических связей;
- в автоматизированном режиме, с помощью процедур анализа содержимого фрагментов контента.
В первом случае потребуется процедура проверки согласованности мнений группы экспертов, а также мнений каждого эксперта в отдельности, с целью исключения циклического упорядочения фрагментов контента. Кроме того, трудоемкость такой процедуры существенно возрастает с увеличением количества фрагментов контента. Автоматизация процесса выявления связей между фрагментами контента позволит снизить общую трудоемкость данного этапа, а также повысить точность определения весов связей.
Для автоматизированного определения связей между фрагментами контента и их весов применяется второй способ, основанный на расчете несимметричных мер включения, характеризующих степень включения одного материала в другой.
Воспользуемся несимметричным коэффициентом Жаккара [10]:
![]() , (3)
, (3)
где ![]() – вектор коэффициентов разложения по базису i-го фрагмента контента.
– вектор коэффициентов разложения по базису i-го фрагмента контента.
Элементы матрицы SА близости фрагментов контента: ![]() (таблица 2).
(таблица 2).
Для формирования траекторий изучения материала на нижнем уровне сначала строятся сети знаний для объектов каждого отдельного кластера с использованием матрицы несимметричных мер включения. Для каждого из трех кластеров (2) построены сети знаний (рис. 1), в узлах которых расположены фрагменты контента, связи обладают весом, показывающим близость фрагментов между собой, а также направлением, характеризующим их дидактическую упорядоченность.
Таблица 2. Матрица несимметричных мер включения для фрагментов контента Cn
|
|
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
|
C1 |
1 |
0.556 |
0.75 |
0 |
0.167 |
0.273 |
0.4 |
0.167 |
|
C2 |
0.714 |
1 |
0.714 |
0.091 |
0.2 |
0.2 |
0.2 |
0 |
|
C3 |
1 |
0.714 |
1 |
0 |
0.2 |
0.2 |
0.333 |
0.091 |
|
C4 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
C5 |
0.333 |
0.333 |
0.333 |
0.143 |
1 |
0.143 |
0.333 |
0.143 |
|
C6 |
0.6 |
0.333 |
0.333 |
0 |
0.143 |
1 |
0.6 |
0.143 |
|
C7 |
0.667 |
0.25 |
0.429 |
0 |
0.25 |
0.429 |
1 |
0.25 |
|
C8 |
1 |
0 |
0.333 |
0 |
0.333 |
0.333 |
1 |
1 |
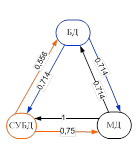
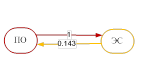
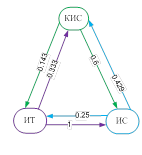
Рис. 1. Сети знаний для трех кластеров.
Как правило, топология каждой или одной из таких подсетей близка к случаю полного графа. Тогда актуальной становится задача выделения наиболее важных связей и «отбрасывания» наименее существенных. С целью выделения наиболее весомых связей строится минимальный каркас. Для этого в качестве веса выбирается расстояние относительно несимметричных мер включения, определяемое как дополнение их до единицы, и строится минимальный каркас, используя все наиболее важные связи. Затем полученный каркас рассматривается как сеть знаний, которая характеризуется отсутствием направленных циклов и транзитивных связей (рис. 2).
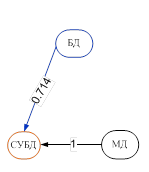
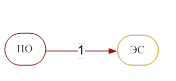
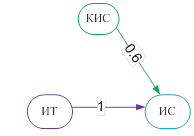
Рис. 2. Минимальные каркасы – сети знаний кластеров без циклов.
На основе обработки сети знаний предложена процедура определения последовательности освоения учебно-справочных материалов. Поскольку сеть знаний является взвешенным орграфом, то к ней применимы алгоритмы на графах. В терминах теории графов построение траектории соответствует построению простой цепи, т.е. такого маршрута, у которого все ребра различные и не содержится одинаковых вершин. Наиболее близким к задаче упорядочения данной сети является алгоритм топологической сортировки графа. Введем на вершинах графа частичное отношение порядка, а именно: вершина i считается меньше чем вершина j, если в графе есть ребро из i в j, т.е. есть связь между фрагментами контента Сi и Сj. Задача топологической сортировки состоит в том, чтобы построить для данного графа такой порядок обхода его вершин, чтобы «меньшая» вершина стояла в этом порядке позже, чем «большая» [3]. Таким образом, будет получена траектория освоения материала (рис. 3). Недостаток данного алгоритма в том, что он не учитывает веса связей, а только их направления. Поэтому для формирования траектории освоения материала предварительно потребовалось построить минимальные каркасы и к ним применять топологическую сортировку таким образом, чтобы вес связей был учтен на «подготовительном» этапе.
[МД]–>[БД]–>[СУБД]
[ПО]–>[ЭС]
[ИТ]–>[КИС]–>[ИС]
Рис. 3. Траектории освоения материала нижнего уровня.
На четвертом этапе необходимо построить траектории верхнего уровня, т.е. упорядочить кластеры, полученные на втором этапе. Для этого построим сеть знаний, узлами которой будут полученные кластеры. Для определения связей между кластерами и их весов воспользуемся несимметричными коэффициентами Жаккара, рассчитанными на третьем этапе. Рассмотрим связи, которые соединяют объекты, вошедшие в разные кластеры.
Пусть множество таких связей ![]() . Разделим его на подмножества
. Разделим его на подмножества ![]() , каждое из которых содержит связи, направленные от одного кластера (кластера
, каждое из которых содержит связи, направленные от одного кластера (кластера ![]() ) к другому (кластеру
) к другому (кластеру ![]() ). Количество
). Количество ![]() таких подмножеств будет равно количеству упорядоченных пар полученных кластеров, т.е.:
таких подмножеств будет равно количеству упорядоченных пар полученных кластеров, т.е.: ![]() , где
, где ![]() – количество кластеров, полученных на втором этапе. Другими словами, суммы элементов подмножеств
– количество кластеров, полученных на втором этапе. Другими словами, суммы элементов подмножеств ![]() , т.е.
, т.е. ![]() также можно рассматривать как несимметричные характеристики сходства, на основе которых может быть построена сеть знаний с кластерами в узлах (рис. 4а). Используя вышеописанную процедуру упорядочения элементов сети знаний (т.е. построение минимального каркаса и последующей его топологической сортировки), можно получить последовательность освоения тем, т.е. траекторию верхнего уровня (рис. 4 б, в).
также можно рассматривать как несимметричные характеристики сходства, на основе которых может быть построена сеть знаний с кластерами в узлах (рис. 4а). Используя вышеописанную процедуру упорядочения элементов сети знаний (т.е. построение минимального каркаса и последующей его топологической сортировки), можно получить последовательность освоения тем, т.е. траекторию верхнего уровня (рис. 4 б, в).
а)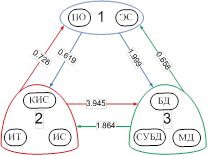 б)
б)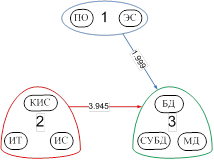 в) [2]–>[1]–>[3]
в) [2]–>[1]–>[3]
Рис. 4: а) сеть знаний с кластерами в узлах, б) её минимальный каркас,
в) траектория верхнего уровня.
В результате автоматически сформированная последовательность освоения учебно-справочных материалов может быть представлена оглавлением:
Тема 1
1.1 Информационные технологии.
1.2 Корпоративные информационные системы.
1.3 Информационные системы.
Тема 2
2.1 Предметная область.
2.2 Экспертные системы.
Тема 3
3.1 Модель данных.
3.2 Базы данных.
3.3 Система управления базами данных.
Применение автоматизированных процедур индексации и кластеризации фрагментов учебного контента позволяет выявить, а также представить в наглядном виде взаимосвязи этих фрагментов, их тематическую близость, построить сеть знаний фрагментов контента и траектории освоения материала.
Рецензенты:
Милов В.Р., д.т.н., профессор, заведующий кафедрой «Электроника и сети», Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Нижегородский государственный технический университет им. Р.Е. Алексеева», Минобнауки России, г. Нижний Новгород.
Мисевич П.В., д.т.н., профессор, профессор кафедры «Вычислительные системы и технологии», Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Нижегородский государственный технический университет им. Р.Е. Алексеева», Минобнауки России, г. Нижний Новгород.



