Введение
Руднотермические печи (РТП) являются основным агрегатом для расплавления руд, в том числе для получения широкой номенклатуры ферросплавов, необходимых в черной металлургии. Суммарная мощность таких установок в России составляет около 1,5 ГВА, поэтому задачи энергосбережения при работе такого оборудования достаточно актуальна. Электроэнергия в рабочее пространство РТП передается по вторичному токоподводу, называемому также короткой сетью, рациональное проектирование которого обеспечивает эффективность использования электроэнергии.
Основными условиями, которым должна удовлетворять короткая сеть руднотермической печи, являются: минимальные активные и индуктивные сопротивления фаз и их симметрия. Реактивное сопротивление короткой сети в значительной степени ухудшает электрические показатели печи и приводит к загрузке источников ее питания большой реактивной мощностью. Активное сопротивление вторичного токоподвода определяет величину электрического КПД печи. Асимметрия параметров фаз приводит к неравномерному выделению мощности в рабочем пространстве, что влечет за собой ряд негативных последствий, в том числе снижение производительности установки.
Наиболее распространенной для круглых трехэлектродных печей является схема вторичного токоподвода «треугольник на электродах». Она характеризуется тем, что преобразование схемы треугольника в звезду осуществляется непосредственно на электродах, а, значит, до электродов протекают токи полуфаз в соответствии с компоновкой выводов трансформатора (рис. 1).
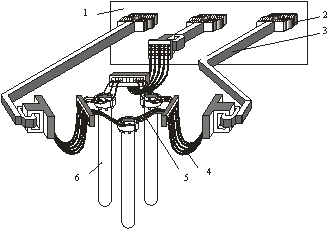
Рис. 1. Эскиз вторичного токоподвода трехэлектродной руднотермической печи: 1 – печной трансформатор; 2 – компенсаторы; 3 – шинопакет; 4 – гибкий токоподвод; 5 –трубки электрододержателя; 6 – электрод.
Современные мощные руднотермические печи в конструкции вторичного токоподвода имеют жесткий неподвижный участок (см. рис. 1, поз. 3), выполняемый в виде пакета прямоугольных шин или водоохлаждаемых трубошин. Зачастую он является самым протяженным из всех участков короткой сети. Его сопротивление составляет порядка 30 % короткой сети. Именно на этом участке формируется несимметрия токоподвода за счет разности длин шинопакетов крайних и средней фаз. Следовательно, актуальна задача проектирования шинопакетов с рациональными параметрами.
Постановка задачи
Существующая на данный момент методика расчета активного и индуктивного сопротивлений вторичных токоподводов мощных электротехнологических установок обобщена в справочной литературе [2, 4]. Она была разработана на основе математического аппарата и программного обеспечения, существовавшего до 1980-х годов. Эта методика имеет ряд допущений. При вычислении активного и индуктивного сопротивления, взаимной индуктивности проводников, произвольно расположенных в пространстве, не учитывается распределение плотности тока по сечению проводника; при расчете активного сопротивления влияние электромагнитного поля учитывается коэффициентом добавочных потерь, вычисляемым лишь для ограниченного набора геометрических параметров взаимодействующих проводников. Эта методика в принципе позволяет с достаточной степенью точности рассчитать индуктивное сопротивление системы проводников [1], что нельзя сказать относительно активного сопротивления. Считается, что активное сопротивление много меньше индуктивного, поэтому повышать точность его расчета нецелесообразно.
В настоящий момент разработан ряд прикладных программ, базирующихся на решении систем дифференциальных уравнений. Они позволяют решать уравнения Максвелла, описывающие электромагнитное поле. В настоящей работе моделировалось электромагнитное поле системы проводников с токами с целью определения их активного и индуктивного сопротивления. Для этого использовался прикладной пакет ANSYS v 14.0 [5].
В работе исследовались шинопакеты жесткого токоподвода руднотермических электропечей – наиболее длинная неподвижная часть короткой сети. Его выполняют в виде набора прямоугольных шин или водоохлаждаемых трубошин. В шинопакете осуществляют перешихтовку проводников, так как это приводит к заметному уменьшению индуктивного сопротивления за счет бифиляции.
Пакеты из прямоугольных шин
Один из вариантов конструкции шинного моста руднотермической электропечи - ряд прямоугольных шин. Чаще всего чередуются проводники, несущие токи прямой и обратной фазы. В работе также исследован вариант попарного чередования шин полуфаз.
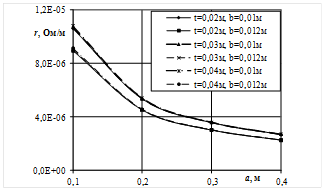
Для различных значений количества шин (n = 4, 8, 12), межцентрового расстояния (t = 0.02; 0.03; 0.04 м), высоты шины (а = 0.1; 0.2; 0.3; 0.4 м), толщины шины (b = 0.01; 0.012 м) были проведены многовариантные расчеты активного и индуктивного сопротивлений шинопакетов обоих вариантов перешихтовки на численной модели. Результаты исследования приведены на рис. 2.
 а)
а)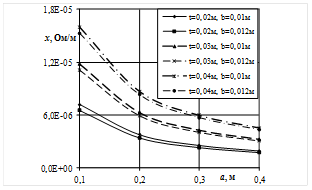 б)
б)
 в)
в)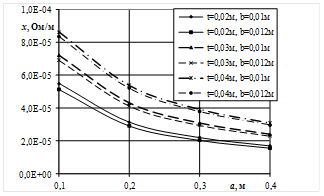 г)
г)
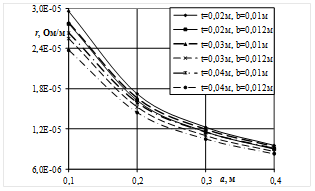
Рис. 2. Зависимость активного (а, в) и индуктивного сопротивления (б, г) шинопакета от высоты шин a при изменении толщины шин b межцентрового расстояния t при фиксированном количестве шин в пакете n=8 при чередовании (а, б) и попарном чередовании (в, г) шин полуфаз.
Сравнивая результаты для разных вариантов перешихтовки, можно отметить, что, при чередовании проводников полуфаз бифиляция более выражена, и значения индуктивного сопротивления заметно ниже, чем при попарном чередовании. Этим объясняется предпочтение именно этой схемы. Согласно методике [2], активные сопротивления обоих вариантов должны быть равны вследствие одинаковости геометрии системы. Однако же полученные значения активного сопротивления для двух вариантов перешихтовки не совпадают. Напрашивается вывод о том, что методика [2] при расчете активного сопротивления не учитывает неравномерности распределения тока по проводникам шинопакета и разности фаз между проводниками.
Следует отметить, что при всех рассмотренных сочетаниях исходных данных активное сопротивление соизмеримо с индуктивным сопротивлением, хотя принято считать, что активное сопротивление настолько мало, по сравнению с индуктивным сопротивлением, что его можно не учитывать.
По рис. 2, а видно, что с увеличением расстояния между рядами проводников в пакете t, активное сопротивление не изменяется. Это связано с тем, что расстояние между шинами намного меньше размера сторон шин, которыми они обращены друг к другу. Изменение расстояния между шинами в рассматриваемых пределах слабо влияет на проявление эффекта близости. Рис. 2, б показывает, что с увеличением расстояния между проводниками в пакете t индуктивное сопротивление возрастает. Это связано с тем, что при увеличении параметра t степень бифиляции уменьшается, что приводит к росту индуктивного сопротивления.
Пакеты трубошин
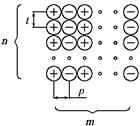
Варианты перешихтовки проводников кольцевого сечения приведены на рис. 3. Для фиксированной геометрии медных трубошин (наружный диаметр 50 мм, толщина стенки трубы 10 мм) были проведены многовариантные расчеты активного и индуктивного сопротивлений для каждого случая перешихтовки на численной модели, созданной с помощью прикладного пакета ANSYS. В расчетах варьировались: количество проводников в вертикальных и горизонтальных рядах n=1, 2,…, 8 и m=2, 3,…, 8, расстояния между горизонтальными и вертикальными рядами t=0,055 ¸0,1м и p=0,055 ¸0,1м, при наружном диаметре трубошин d =0,05 м и толщине стенки 0,01 м. На рис. 4 приведены результаты расчетов для шахматного и коридорного вариантов перешихтовки.
 а)
а) 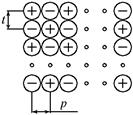 б)
б) 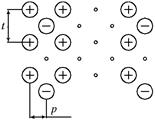 с)
с)
Рис. 3. Варианты перешихтовки многофазных пакетов трубошин: а) коридорный, б) шахматный, в) коридорный со смещением по вертикали.
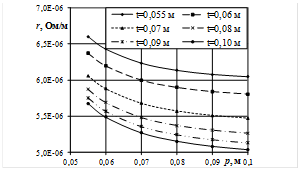
Следствием допущений методики [2] является равенство активных сопротивлений шахматного и коридорного вариантов перешихтовки. Результаты исследования это не подтверждают (см рис. 4, а и в). Это доказывает, что разность фаз и неравенство токов проводников влияют как на их индуктивное, так и на их активное сопротивление.
 а)
а)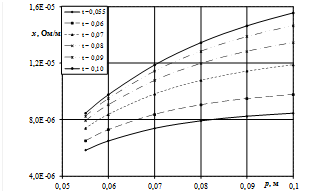 б)
б)
 в)
в)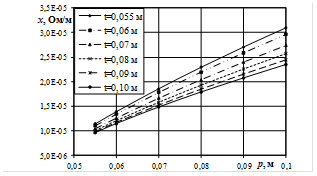 г)
г)
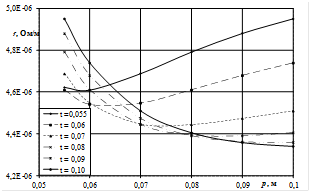
Рис. 4. Зависимость активного (а, в) и индуктивного (б, г) сопротивления шинопакета при изменении горизонтального расстояния p между трубошинами при фиксированных значениях вертикального расстояния t между трубошинами (n = m = 4), для шахматного (а, б), коридорного (в, г) способов перешихтовки
На рис. 4, а видно, что при варианте рис. 3, б активное сопротивление минимально при равенстве горизонтального и вертикального расстояний между центрами проводников.
Рис. 4, г показывает, что с увеличением расстояния между рядами проводников в пакете в горизонтальном направлении - p индуктивное сопротивление возрастает, в то время как при увеличении расстояния в вертикальном направлении - t оно уменьшается. Описанное поведение сопротивлений характерно для шинопакетов, изображенных на рис. 3, а и 3, в. Это связано с тем, что при увеличении параметра p отрицательная взаимоиндуктивность уменьшается по абсолютной величине, что приводит к росту индуктивного сопротивления. Увеличение параметра t приводит к уменьшению положительной взаимоиндуктивности проводников соседних горизонтальных рядов, что вызывает уменьшение индуктивного сопротивления фазы шинопакета.
Установлено, что при n ³ 6 и m ³ 2 (наиболее применяемое соотношение в реальных установках) активное сопротивление становится соизмеримым с индуктивным сопротивлением (r < x менее, чем в 2,5 раза), хотя принято считать, что активное сопротивление настолько мало, по сравнению с индуктивным сопротивлением, что его можно не учитывать.
Аналогичные исследования были проведены для трубошин с наружным диаметром 0,06 м. Они показали, насколько изменение диаметра трубошин влияет на активное и индуктивное сопротивления пакета в целом. При увеличении внешнего диаметра с 0,05 м до 0,06 м уменьшение активного сопротивления составляет около 10%. Активное сопротивление падает за счет увеличения площади сечения, при этом увеличивается периметр сечения трубошин, а, значит, уменьшается их собственная индуктивность.
Выполнен сравнительный анализ результатов, полученных численным моделированием, рассчитанных по традиционной методике [2], на основе каскадных схем замещения [3]. Сравнение показывает, что количественные различия составляют от 10 до 30%. Следует отметить, что результаты расчета активного сопротивления дает только метод численного моделирования.
Результаты данного исследования были аппроксимированы зависимостями, позволяющими достаточно точно и просто проводить расчеты активного и индуктивного сопротивлений шихтованных шинопакетов. Такие зависимости существенно упрощают процесс расчета электрических параметров данного участка, позволяют быстро оценивать множество вариантов, уравнивать сопротивления пакетов шин разных фаз за счет изменения способа перешихтовки, количества, размеров проводников и расстояний между ними.
Выводы
Разработанный метод исследования позволил сформировать массив данных, охватывающий большое многообразие вариантов исполнения шинопакетов. При этом численное решение уравнений электромагнитного поля с помощью современного программного обеспечения позволяет для реальных конструкций токоподвода учитывать все возможные эффекты: поверхностный, близости, краевой, неравномерность распределения тока по параллельным проводникам и т.п.
Полученные результаты позволяют существенно уточнить расчет активного сопротивления и упростить методику расчета индуктивного сопротивления шинопакетов.
Работа выполнена в рамках Программы стратегического развития НГТУ.
Рецензенты:
Аньшаков А.С., д.т.н., профессор, главный научный сотрудник Института теплофизики им. С.С. Кутателадзе СО РАН, г. Новосибирск.
Урбах Э.К., д.т.н., ведущий научный сотрудник Института теплофизики им. С.С. Кутателадзе СО РАН, г. Новосибирск.



