В последние десятилетия социально-экономические отношения в России претерпевают значительные изменения. Человек получил больше возможностей для реализации своих способностей, самовыражения и самоактуализации, стал более открытым для общения и выбора жизненных ситуаций. Подрастающее поколение стало более нетерпимым к проявлениям догматизма, отсутствию гибкости в обучающих воздействиях, стало более прагматично и осознанно оценивать перспективы своей будущей жизни. Для студента - будущего учителя, в этом направлении особенно важно показать единство учебного предмета (математики), его генезис, исходя из практических потребностей человека, красоту и гармонию математического знания, его существенное влияние на прогресс и комфортное развитие человечества. В то же время студенту надо дать возможность почувствовать и освоить технологию наглядного моделирования [1] устойчивых базисных блоков математического знания, образующих фундирующие модусы развития [2], воспроизводимых и значимых в формировании мотивационной сферы, опыта личности, творческой активности [3]. В то же время, интеллектуальные операции мышления (моделирование, понимание, конкретизация, абстрагирование, обобщение и т.п.), лежащие в основе универсальных учебных действий обучаемых, эффективно могут развиваться только в процессе освоения взаимодействующих разделов математического знания.
Будущий и настоящий учитель математики должен освоить единство математического знания не только с методологических, философских и теоретических позиций, но и технологически осмыслить серию конкретных проблем математики, решаемых комплексом математических методов различных дисциплин. Выявление интегративного единства математики как науки и как педагогической задачи невозможно без содержательного и процессуального анализа научного познания - деятельности, направленной на производство и воспроизводство объективно истинного знания и требующей соответствующего мышления для своего осуществления. Выявление, возникновение и понимание науки в ее целостном виде на основе актуализации базовых интегративных связей становится важным методологическим аспектом анализа генезиса научного мышления и научной деятельности. В научном познании мыслительные действия направлены на исследование глубинной сущности реального мира, связей и отношений его вещей и процессов, законов его существования и развития. Для такого обучения необходима организация учебной деятельности в единстве самостоятельного освоения больших массивов естественнонаучного, информационного и математического знания на основе наглядного моделирования в сочетании с элементами дистанционного обучения и развертывания фундирующих процедур освоения математики. При этом, необходимо понимать, что математический аппарат предназначен, в том числе и для описания целостных систем, функционирующих в реальном мире; он описывает их структуру и динамику, статику и интегральные характеристики на основе математического моделирования. В то же время, математические понятия, теоремы, алгоритмы, доказательства и т.п., будучи объектами педагогического процесса обучения математике, должны приобретать свойства и характеристики целостности как основы сохранения, обработки и переноса информации новому поколению.
Современный этап развития науки характеризуется усилением и углублением взаимодействия отдельных её отраслей, формированием новых форм и средств исследования, в т.ч. математизацией и компьютеризацией познавательного процесса. Распространение понятий и принципов математики в различные сферы научного познания оказывает существенное влияние как на эффективность специальных исследований, так и на развитие самой математики. В процессе познания действительности математика играет все возрастающую роль. Сегодня нет такой области знаний, где в той или иной степени не использовались бы математические понятия и методы. Проблемы, решение которых раньше считалось невозможным, успешно решаются благодаря применению математики, тем самым расширяются возможности научного познания. Современная математика объединяет весьма различные области знания в единую систему. Этот процесс синтеза наук, осуществляемый на лоне математизации, находит свое отражение и в динамике понятийного аппарата. Так, применение математики в механике, астрономии, физике и других областях естествознания, с одной стороны, способствовало проникновению в научный аппарат указанных областей знания таких понятий, как число, функция, производная, дифференциал, интеграл, структура, система и т.д., с другой - привело к формирования основ дифференциального интегрального исчисления, теории вероятности, теории множеств и целого ряда других направлений математики. Использование математики в биологических и особенно гуманитарных науках содействовало образованию необычных для классической математики понятий как: качество, расплывчатое множество, функция принадлежности, отображение, бинарное отношение, алгебраические операции и др. Способы и методы математического мышления наделены потенциальными синтетическими возможностями. Эвристическое взаимодействие качественных и количественных, содержательных и формальных методов исследования составляет объективную основу математизации научного знания. В этом процессе материалистическая диалектика выступает как методологическая основа математизации всего научного знания, его интеграции. Актуализация этих интеграционных процессов придает математической науке целостный характер и внутреннее единство идей, методов, понятий и теорем, алгоритмов и процедур.
В нынешних условиях, когда математические методы находят широкое применение не только в естествознании, технике и смежных науках, но и в экономике, гуманитарных науках, то это непременно должно быть отражено в программах школьного и вузовского математического образования. Важной является также проблема более активного включения психофизиологических механизмов целостного восприятия информации обучаемым, развития интеллектуальных операций мышления, его математических способностей, мышления и культуры.
Методика. В последние десятилетия математика как педагогическая задача испытывает беспрецедентное давление со стороны общества как по поводу содержания обучения, так и относительно методов ее преподавания. Дело в том, что глубина формализации даже в естественных приложениях и следование внутренним закономерностям строения здания математики входят в противоречие с онтогенезом развития и социализации отдельного индивида, так и с потребностями общества по обеспечению своей жизнедеятельности. Поэтому обучение математике и содержание математического образования как в средней, так и в высшей школе, должны пересматриваться в направлении большей визуализации, наглядного моделирования и раскрытия социального статуса математики на основе целенаправленного раскрытия структуры её внутренних и внешних взаимосвязей, актуализируя при этом интегральные конструкты как дидактические единицы.
Основным средством, способствующим появлению новообразований, является моделирование как высшая форма знаково-символической деятельности, ведущая к появлению нового знания о природе и технологических процессах в производстве, о законах общественного развития и закономерностях мышления, восприятии и памяти человека. Будущий учитель математики должен не только освещать подобные вопросы, но и владеть особой структурой профессиональных умений и навыков оперирования с математическими объектами.
Рассмотрение генезиса учебного элемента как педагогической задачи, то есть как объекта для усвоения другим субъектом в будущей учебной деятельности, требует учета не только своего ментального опыта, личностных характеристик и психолого-педагогических условий деятельности, но и системного анализа функционирования аналогичных подструктур будущего субъекта усвоения социального опыта в изменившихся педагогических условиях. К тому же, целенаправленный процесс перехода социального опыта, накопленного предшествующими поколениями в содержании данного учебного предмета (объекты, явления и процессы), в опыт индивидуальный при активном поведении субъекта в процессе усвоения сопровождается необходимыми атрибутами когнитивного процесса: понимание, представление, локализация, целостность и др., вложенных в процесс профессионализации.
На следующем рисунке (см. рис.1), показаны структура и элементный состав факторов, влияющих на проектирование математического объекта (процесса, явления) как педагогической задачи.
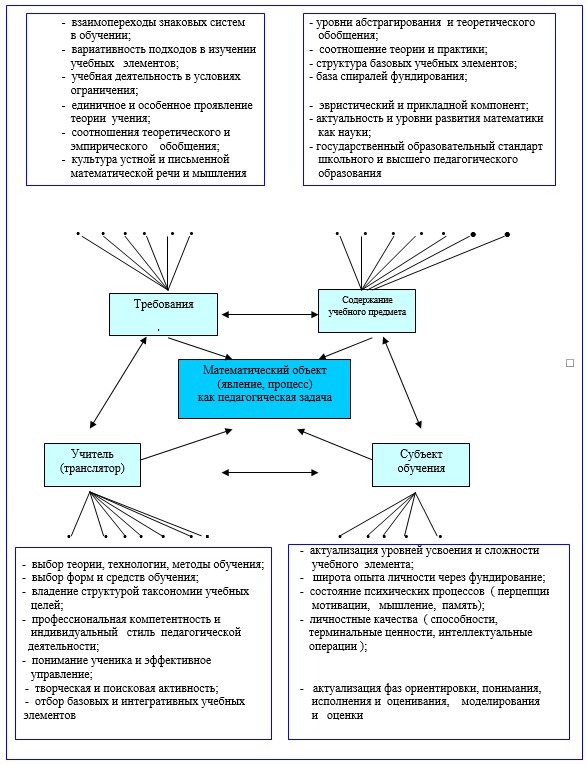
Рис.1. Факторы и характеристики проектирования сущности математики как педагогической задачи
Рассматривая математику как педагогическую задачу, приходится сталкиваться с проблемами адекватного представления, различения, становления, устойчивости восприятия и воспроизведения математического знания и выявления специфических особенностей феномена математического мышления. В последние десятилетия возникла принципиально новая ситуация, благоприятствующая реальным шагам к возрастанию интереса к математике, в том числе как педагогической задаче и эффективному средству развития интеллекта школьников и студентов. Этому способствовали следующие факторы:
- глубокая озабоченность учеников, родителей, педагогов содержанием математического образования и его влиянием на развитие личности;
- демократизация и гуманизация образовательных процессов в школе и вузе, выдвижение на первый план проблем личностного развития школьников, особенно в период формирования онтогенетических новообразований в мышлении;
- расширение информационных средств обеспечения учебного процесса: дисплейные классы, Internet, сервисные программные продукты, мультимедиа, дистанционное обучение и т.д.;
- интенсивное развитие методологических основ обеспечения педагогических процессов: психология и физиология человека, искусственный интеллект, инженерная психология и психология индивидуальной и совместной деятельности, теория управления и теория образовательных систем и т.д.
Как рассказать школьнику, что большая теорема Ферма, над которой триста лет бились лучшие умы человечества, доказана А.Вайлсом в 1995 году, а трисекция угла и квадратура круга невозможны с помощью циркуля и линейки? Как наиболее эффективно развить мыслительные операции ученика (логику, анализ, синтез, обобщение, конкретизации, аналогии и т.п.) в процессе обучения математике, которая объективно должна являться самым мощным развивающим средством (и чего не наблюдается в настоящее время)? Как должна быть отражена в обучении математики ее роль в жизнедеятельности общества и в развитии других наук, в том числе в обосновании космических полетов и безопасности воздушных перевозок? Как показать, что физика - мощный поддерживающий компонент жизнедеятельности и мировоззрения, который без знания и использования математики есть просто наблюдение и эксперимент, а психология без использования статистических методов обработки и анализа экспериментальных данных и моделирования психических процессов есть тенденция к внешней феноменологии и эмпиризму без вскрытия внутренних, сущностных механизмов психических процессов.
Будущий учитель математики должен не только освещать подобные вопросы, но и владеть особой структурой профессиональных умений и навыков оперирования с математическими объектами.
Особое место в современном образовании занимают информационные технологии: мультимедиа, дистанционное обучение, телекоммуникации, графические калькуляторы и т.п. В этой связи необходимо четко расставить акценты относительно возможности профессиональной подготовки учителя: информационные технологии как средство обучения - да, информационные технологии как структурообразующий фактор педагогической системы - да, дистанционное обучение как парадигма в подготовке учителя, альтернативная личности преподавателя, - нет (по крайней мере, на данном этапе развития средств коммуникации и информационного обмена). В обоснование последнего положения приведем следующие аргументы:
- неуправляемое становление приемов мыслительной деятельности, именно это фактор привел к неудовлетворительным результатам реализации идей программированного обучения (Э. Торндайк, Б. Скиннер, Н. Краудер и др.) в 1960-1970-х гг. Причиной неудач стал необоснованный перенос принципов научения животных на процесс обучения человека с его специфическими особенностями. Н.Ф Талызина объясняет неудачи скиннеровского подхода выбором неадекватной психологической теории;
- отсутствие реального (а не интерактивного) взаимодействия учителя с учениками, между учениками, вследствие чего исключается возможность активизации направленных и взаимообусловливающих полифункциональных факторов адекватного восприятия новой информации: перцептивных, мнемических, эмоциональных, волевых и т.п.;
- нарушение целостности интериоризации визуально-логического ряда перцептивных образов новой информации вследствие искусственного ограничения поля восприятия и динамики обращения с репертуаром кратковременной и долговременной памяти.
Все это относится к дистанционной и очной формам обучения в области профессионально - предметного блока подготовки и переподготовки учителя математики; естественно, что увеличение временных периодов для дистанционных форм обучения, создание специфических дидактических методов, совершенствование средств коммуникации, вероятно, смогут компенсировать отмеченные недостатки.
Содержание учебной дисциплины « Фундирование опыта наглядного моделирования на основе единства математики в задачах» базируется на материале всех основных школьных и вузовских математических курсов (алгебры, математического анализа, геометрии, стохастики, математической логики), согласуясь с Государственным образовательным стандартом высшего педагогического образования по специальности 032100 «Математика», а также, подготовки бакалавров и магистров физико-математического направления ФГОС третьего поколения, и своей первоочередной задачей ставит углубление и структурирование педагогического опыта учителей математики в направлении актуализации личностных конструктов и овладение приемами формирования обобщенных учебных действий и интеллектуальных операций у школьников [4]. При этом, учебно-познавательная деятельность практикующих учителей актуализируется на поиск, анализ, выявление механизмов и существенных интеграционных связей в математике и методике ее преподавания на основе профессионально-ориентированного и исследовательского подхода. Познавательная деятельность учителя связана с формированием, становлением и развитием ключевых профессиональных компетенций учителя математики в таких направлениях как: проектный метод исследования, метод опережающего отражения при проведении практических занятий, освоение приемов организации работы в малых группах учащихся, формирование устойчивой мотивации к изучению и освоению современного состояния математики, и вообще, проблем в математическом образовании на мировом уровне [5]. В основе учебной дисциплины лежит исследование интегративных связей в математике и их переноса в дидактическое поле формирования приемов научного познания и устойчивой учебной мотивации у школьников в контексте рассмотрения и исследования так называемых интегративных задач (генезис, содержание, анализ, применение, оценка, презентация), выбор которых осуществляется выявлением обоснованных критериев.
Изложение учебного материала сопровождается поисковой и творческой активностью будущих учителей математики в направлении профессионализации, обогащении и фундирования опыта и развития личностных качеств основе актуализации компетентностного подхода.
Цели учебного курса:
♦ расширить объем и оптимизировать структуру профессионально-ориентированных математических знаний на основе актуализации личного педагогического опыта и активизации интеграционных связей в математике разных уровней (в том числе, школьного и вузовского знания) и использования информационных технологий, генерируя при этом фундирующие конструкты иерархических банков прикладных, исследовательских и учебных задач;
♦ актуализировать базовые современные математические методы исследования реального мира: наглядное моделирование, аксиоматический метод, экспериментальный метод, содержательного обобщения, аналогии, инверсии и др. - на основе компетентностного, системо- генетического и синергетического подходов и эффективного использования информационных технологий;
♦ практиковать исследовательский метод в освоении содержания учебного курса (и интеграции информационных, естественнонаучных и гуманитарных знаний) на основе личностных предпочтений, диалога культур и развития диагностических способностей, включая основные этапы научного познания: наблюдение опыта, исследование опыта, рефлексивные процессы, наглядное моделирование и объяснение опыта, презентация, анализ и оценка полученных результатов;
♦ показать учителю значимость, красоту и единство математики как науки на основе современного ее состояния и приложений, включая интеграционные взаимодействия понятий, теорем, методов, идей, алгоритмов и процедур различных дисциплин: алгебры, геометрии, математического анализа, стохастики, математической логики, - на различных уровнях фундирования и интеграции математических знаний;
♦ развить обобщенные навыки и приемы, интеллектуальные операции, творческие и логические акты, принципы и стили научного мышления и научного общения в совместной деятельности учителей и управлением познавательной деятельностью школьников ( в том числе, в малых группах) на основе актуализации личностного опыта, диалога культур и интеграционных фундирующих связей в математике: моделирование, понимание, индукция, дедукция, инсайт, аналогии, инверсия и антиципации. Содействовать при этом выявлению и становлению индивидуального стиля деятельности педагога на основе концепции фундирования.
Задачи учебного курса:
♦ разработать и реализовать методику исследования интеграционных связей в математическом объекте (МО) (раздел, тема, процедура, теорема, алгоритм, понятие) на основе разработанных критериев отбора:
♦ наличие и возможность актуализации в МО 3 - 4 интегративных связей разного уровня между учебными предметами: алгебра, геометрия, математический анализ, стохастика, математическая логика;
♦ возможность наглядного моделирования процедуры (алгоритма) актуализации существенных связей в МО;
♦ содержательность и мотивационная составляющая истории и генезиса
состояния существенных связей МО;
♦ доступность и возможность воспроизведения учителем рассматриваемых процедур (алгоритмов) и приемов формализации исследуемого МО;
- возможность проектирования интеграционных связей и существа МО на содержание и методику обучения математике в средней школе;
- наличие новых (по отношению к ГОС) математических знаний, методов, алгоритмов или процедур в содержании исследуемого МО;
♦ отобрать 5-7 МО, удовлетворяющих вышеперечисленным критериям, и создать дидактические условия их освоения обучаемыми из расчета 3 лекционных часа на освоение одного МО;
♦ практическое исследование технологической процедуры анализа интеграционных связей МО (10 конкретных проблем) малыми группами учителей (2-3 человека) с текущей презентацией на практических занятиях по специальному графику и с использованием методики опережающего отражения для проведения расчетных работ и использования информационных технологий ( графические калькуляторы, компьютерные математические системы: Maple, Mathematica, MathCАD, MathLab, Derive, системы динамической геометрии Cabri, GeoGebra, Aftograph и т.п.);
♦ разработка проектов интегративных исследований МО (5 проектов) группами учителей по 10-12 человек с актуализацией приемов научной деятельности и общения, презентацией результатов и использованием POWER POINT на основе дифференциации исследовательской деятельности.
Содержание и структура учебной деятельности будущих учителей
Учебно-исследовательская деятельность студентов по освоению учебной дисциплины подразделяется на три вида деятельности:
- освоение методологии, методов, приемов и технологии исследовательского поведения в процессе поиска и актуализации интегративных связей в математике на основе актуализации и фундирования личного педагогического опыта [6];
- работа в малой группе в разработке анализа, решения, моделирования и оценки исследовательских задач с использованием информационных технологий и современных тенденций в математике;
- проведение проектного исследования генезиса, содержания и модели интеграционных связей математического объекта с презентацией на основе технологии POWER POINT [7; 8; 9].
Содержание и структура инновационной деятельности учителя в процессе освоения математического знания в его единстве на основе развертывания фундирующих процедур представлена на следующей модели (Рис.2).
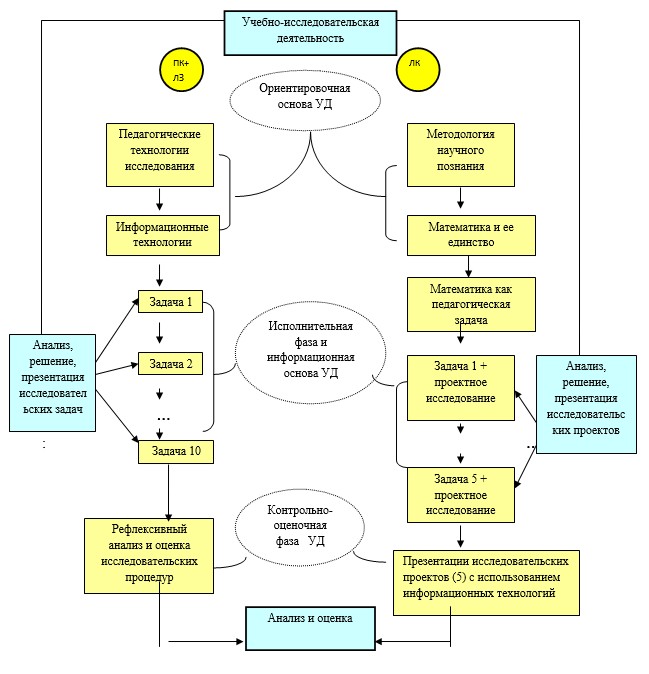
Рис.2.Содержание и структура инновационной деятельности учителя в процессе освоения математического знания
Выводы
Согласно Е.И. Смирнову [10], процесс фундирования математических знаний заключается в создании педагогических, психологических и организационных условий для поэтапного и диагностируемого развертывания единой сущности знания, необходимых математических структур, операций и процедур, с эффектом личностного развития обучаемого. Таким образом, в процессе поэтапного развертывания концептуальных, естественнонаучных, информационных и математических моделей реальных явлений и процессов в ходе исследовательской деятельности студенты осваивают фундирующие модусы развития на основе интеграции математических знаний.
Рецензенты:
Афанасьев В.В., д.п.н., профессор, ректор Ярославского государственного педагогического университета им. К.Д.Ушинского, г. Ярославль.
Секованов В.С., д.п.н., профессор, заведующий кафедрой информатики Костромского государственного университета им. Н.А.Некрасова, г.Кострома.



