Введение
Взаимосвязь теории с практикой была и остается одним из основных дидактических принципов естественнонаучного и инженерного образования. Его результативность подтверждается мировой педагогической практикой, а богатейший опыт человечества
в использовании научных достижений при создании технических устройств и технологий, дает обширный предметный материал для формирования у студентов и курсантов умения применять теоретические знания в практических целях [5].
В этой связи совершенствование форм и методов учебной экспериментально-практической и исследовательской деятельности в современном образовании является актуальной задачей. Откуда следует концепция настоящего исследования:
-
Стремительное обновление информационного пространства и современная информационная революция требуют адекватной и непрерывной модернизации учебного процесса преподавания естественнонаучных и инженерных дисциплин и, соответствующей этим дисциплинам, информационной среды учебной деятельности студентов, курсантов и преподавателей вузов.
-
Совершенствование методики и техники учебного эксперимента – важная составляющая модернизации информационной среды учебной деятельности, обеспечивающей формирование у студентов и курсантов умений и навыков исследовательской деятельности.
Цель исследования: модернизация средств и методик проведения учебного вычислительного эксперимента в практике преподавания естественнонаучных и инженерных дисциплин, на примере совершенствования методики проведения электротехнического вычислительного эксперимента
Материал и методы исследования: моделирование процесса обучения на основе использования современных компьютерных технологий, математическое моделирование, обобщение опыта.
Результаты исследования и их обсуждение. Первым шагом практической проверки изучаемой научной теории является решение учебной задачи – абстрактной проблемной ситуации, направленной на прогнозирование поведения некоторого умозрительного гипотетического объекта для вполне определенных и конкретных условий его эволюции. Чтобы прогнозировать поведение гипотетического объекта студенту необходимо:
-
знать обобщенные математические модели элементов, входящих в структуру исследуемого в учебной задаче объекта;
-
знать алгоритм использования обобщенных математических моделей структурных элементов, для составления математических моделей всего объекта;
-
уметь составить математическую модель исследуемого объекта и рассчитать ее, то есть уметь выполнить вычислительный эксперимент.
В практике преподавания естественнонаучных и инженерных дисциплин математические модели, исследуемые в учебных задачах, достаточно объемны и сложны, а их «ручная» математическая обработка требует больших затрат учебного времени, отводимого
на аудиторную и самостоятельную работу студента.
С целью оптимизации использования учебного времени студентов, необходимо научить их использованию возможностей современных программно-аппаратных средств, чтобы на этой основе минимизировать временные затраты на вычислительные операции.
В учебном процессе естественнонаучных и инженерных дисциплин нет избытка времени, позволяющего изучать прикладные программы со сложным интерфейсом. В этой связи, среди большого количества современных программных продуктов, используемых для проведения вычислительного эксперимента, особого внимания заслуживает пакет Mathematica – мощная система компьютерной алгебры с достаточно удобным, интуитивно понятным и простым в освоении интерфейсом.
Mathematica является ведущим программным продуктом для обработки числовых, символьных и графических данных, повсюду используемым профессионалами практически в каждой ветви научных и технических вычислений. Mathematica обходится механизмами математики, поэтому пользуясь ею, студенты могут концентрироваться на содержании и смысле своей работы.
Учебные учреждения всего мира используют пакет Mathematica в университетском образовании. Однако сразу следует отметить высокую стоимость пакета Mathematica, что делает весьма проблематичным его использование российскими студентами. Потому
в нашей работе исследуются возможности применения в учебном вычислительном эксперименте альтернативных, свободных систем компьютерной математики.
В этой связи, нами, в рамках госбюджетной научно-исследовательской работы [3] по теме 7.16/09 «Совершенствование методики и техники учебного электротехнического эксперимента», выполняемой на кафедре Электрооборудования судов в Мурманском Государственном техническом университете, был проведен сравнительный анализ возможностей использования в учебном вычислительном эксперименте ряда альтернативных, свободных систем компьютерной математики.
Для исследования возможности использования альтернативных бесплатных систем компьютерной алгебры в вычислительном электротехническом эксперименте еще во время первого этапа ГБ НИР были сформированы студенческие творческие коллективы (СТК), выполнившие сравнительный анализ возможностей использования в учебном процессе пакетов символьной математики Maxima, Scilab, Axiom и Matlab.
По результатам первого этапа мы остановили свой выбор на пакете Scilab, поскольку сочли его интерфейс наиболее удобным. Интерфейс этого пакета близок к интерфейсу пакета Mathematica. Основное отличие состоит в том, что Scilab предполагает исключительно строчный способ записи математических выражений и команд. Mathematica позволяет более наглядно и привычно вводить в программу информацию: можно использовать надстрочные и подстрочные символы, пакет допускает запись символов интеграла, корней любой степени, запись матриц и т.д.
Наша педагогическая практика показала, что свободно распространяемый пакет символьной математики Scilab обладает рядом достоинств, основными из которых являются:
-
удобный интерфейс, в основе которого интегрированный в Scilab текстовый блокнот, позволяющий передавать текст программы, написанной в блокноте, в командное окно – с целью ее исполнения;
-
возможность выполнения символьных вычислений, позволяющих минимизировать время на ввод начальных условий и математической модели, исследуемой
в вычислительном эксперименте; -
простой язык программирования, очень близкий естественному математическому языку, что минимизирует время на обучение студентов применению этого пакета для решения конкретных учебных задач вычислительного эксперимента;
-
широкие возможности матричных вычислений, широкие графические возможности представления результатов вычислительного эксперимента.
Применение пакета Scilab дает возможность подготовить студентов к выполнению натурного исследования реального процесса или явления в естественных или лабораторных условиях. Обработка результатов натурного эксперимента в среде пакета Scilab также очень эффективна.
Продемонстрируем возможности использования пакета Scilab для графоаналитического анализа нелинейных цепей, на примере расчета неразветвленной магнитной цепи (рис. 1), находящейся под воздействием источника постоянной МДС (магнитодвижущей силы).
Магнитные проводники этой цепи выполнены из электротехнической стали марки Э4АА. Кривая намагничивания стали представлена двумя участками на рис. 2.
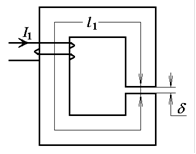
Рис. 1. Исходная схема
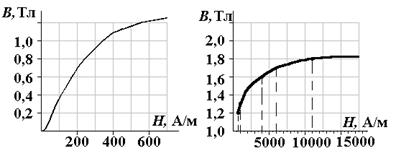
Рис. 2. Кривые намагничивания стали Э4АА
Параметры НМЦ заданы следующими величинами: l1 = 50 см; δ = 0,8 мм; S = 20 см2; w = 800 витков; I1 = 2 A.
Требуется определить величину магнитного потока в сердечнике и магнитное напряжение на воздушном зазоре.
Магнитные цепи описываются теми же математическими моделями, что и нелинейные электрические цепи. Поэтому методы расчета магнитных цепей совпадают с методами расчета нелинейных электрических цепей.
Составим расчетную схему замещения исследуемой цепи, с помощью электротехнических условных обозначений (рис. 3).
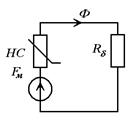
Рис. 3. Схема замещения
Математическая модель этой цепи описывается нелинейным уравнением, составленным на основе второго закона Кирхгофа:
![]()
где Fм – МДС источника. Fм = Iw; UНС – магнитное напряжение на ферромагнитном участке магнитопровода, представленном на расчетной схеме нелинейным сопротивлением НС; Uδ – магнитное напряжение на воздушном зазоре, сопротивление которого Rδ = const.
Алгоритм решения нелинейного уравнения, являющегося математической моделью (ММ) исследуемой магнитной цепи, следующий:
1. На одном графике построить АВХ всех элементов исследуемой магнитной цепи:
-
АВХ ферромагнитного участка исследуемой цепи, строится отображением координат точек кривой намагничивания стали в координатную плоскость UНС (Ф). Абсциссы точек АВХ получают с помощью известного выражения Ф = BS, ординаты – UНС = Hl1;
-
АВХ воздушного зазора выразить из закона Ома Uδ (Ф) = Rδ Ф, где Rδ = δ/(μμ0S);
-
АВХ источника МДС Fм (Ф) – прямая, параллельная оси абсцисс, с ординатой Fм = Iw;
2. Численным или графоаналитическим методом сложить каждую пару ординат магнитных напряжений АВХ UНС(Ф) и Uδ(Ф), имеющих одинаковую абсциссу – одинаковое значение магнитного потока и построить результирующую АВХ для левой части уравнения ММ.
3. Определить искомое нами значение магнитного потока Ф0, действующего
в магнитном сердечнике и в воздушном зазоре, как числовое значение абсциссы точки пересечения результирующей АВХ с АВХ источника МДС;
4. Определить искомое нами Uδ – значение магнитного напряжения на воздушном зазоре, как ординату точки АВХ воздушного зазора Uδ (Ф), имеющей абсциссу, равную найденному значению магнитного потока Ф0.
Реализовать этот алгоритм можно «вручную», с помощью карандаша и линейки, выполняя все построения на миллиметровой бумаге, а сопутствующие вычисление – на калькуляторе. Однако современный инженер должен уметь решать нелинейные задачи, используя современные программно-аппаратные средства. Ниже приведен листинг разработанной нами Scilab-программы расчета исследуемой магнитной цепи.
Листинг Scilab-программы
-
L=0.5;S=20/10000;d=4*0.2/1000,w=800;I=2;
-
Bh=[0 0; 100 0.4; 200 0.7; 300 0.9; 400 1.1; 600 1.2; 5000 1.65; 10000 1.79; 15000 1.81];
-
B=Bh(:,2);H=Bh(:,1);
-
subplot(1,2,1);xtitle('Кривая намагничивания стали Н(В)','B, Тл','H, А/м');
-
plot(B,H,'r*');xgrid(); Alpha=0.1481;Beta=sinh(B(7)/Alpha)/H(7),
-
B01=[0:0.001:1.8];H01=Alpha*sinh(Beta*B01);plot(B01,H01);xgrid();
-
subplot(1,2,2);xtitle(' АBХ стали и воздушного зазора ','Ф, Вб','Um, А');
-
UmSt=L.*H01;Potok=S.*B01;
-
Yd=(4*%pi*S)/(d*10000000) //Магнитная проводимость воздушного зазора
-
UmD=Potok/Yd;plot(Potok,UmD);
-
plot(Potok,UmSt);xgrid();//аппроксимированная ВАХ на стальном участке
-
plot(Potok,I*w,'g');
-
plot(S.*B,L.*H,'r*');xgrid();//ВАХ на стальном участке,
-
plot(Potok,UmD+UmSt,'r');
-
deff('[y]=f(x)','y=Alpha*L*sinh(Beta*x/S)+x/Yd-I*w')
-
x=fsolve(0,f); x, Ud=x/Yd, Unc=L*Alpha*sinh(Beta*x/S), I*w, Ud+Unc
Первые пять строк программного кода позволяют вывести в левую часть графического окна последовательность из девяти красных звездочек, координаты которых соответствуют табличной кривой намагничивания в зависимости H(B), рис. 4.
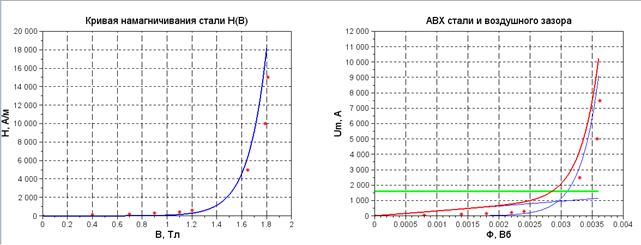
Рис. 4. Вид графического окна. Абсцисса точки пересечения результирующей АВХ (красного цвета) с АВХ источника МДС (зеленого цвета) равна Ф0 = 0,0029 Вб
В шестой строке задается начальное значение коэффициента Alpha=0.1481 и, по координатам одной из точек кривой намагничивания, рассчитывается значение коэффициента Beta=sinh(B(7)/Alpha)/H(7). Далее кривая намагничивания аппроксимируется функцией гиперболического синуса и выводится в графическое окно, в виде кривой синего цвета, поверх табличной кривой. На этом этапе выполняется подбор значения коэффициента Alpha таким образом, чтобы наиболее точно наложить аппроксимированную кривую на табличную. В строках с 7 по 14 выполняется весь алгоритм решения нелинейного уравнения, являющегося ММ исследуемой магнитной цепи. Результат его исполнения выводится в правой части графического окна, рис. 4.
В строках 15 и 16 дан расчет исследуемой цепи численным методом и выполнена проверка решения по второму закону Кирхгофа. В командное окно выведены следующие значения:
- магнитный поток в зазоре и сердечнике x = 0.0028530 (Вб);
- магнитное напряжение на воздушном зазоре Ud = 908.13716 (А);
- магнитное напряжение на ферромагнитном участке Unc = 691.86284 (А);
- МДС Fм = 1600 (А); сумма магнитных напряжений UНС (Ф0) + Uδ (Ф0) = 1600 (А).
Для организации консультаций студентам по использованию пакета Scilab в учебном вычислительном эксперименте был создан учебный сайт (http://af-toe-mgtu.ucoz.ru/), на одной из страниц которого мы выкладываем методические материалы в помощь студентам и курсантам университета, использующим этот пакет.
Заключение
Использование свободно распространяемого пакета Scilab в учебном вычислительном эксперименте естественнонаучных и инженерных дисциплин целесообразно по ряду соображений.
Потенциал предметного содержания естественнонаучных и инженерных дисциплин может быть реализован, при условии активной познавательной деятельности курсантов и студентов по освоению изучаемой дисциплины.
Продуктивное усвоение студентами и курсантами предметного материала дисциплины на основе учебного вычислительного эксперимента определяет мотивационный аспект, формирует познавательный интерес и ценностное отношение к профессиональным знаниям.
Наряду с мотивационным аспектом, практико-ориентированное обучение естественнонаучным и инженерным дисциплинам обеспечивает инженерному образованию содержательный и процессуальный аспекты, способствует повышению уровня физического осмысления процессов, протекающих в изучаемых технических устройствах. Практико-ориентированное обучение позволяет достичь более глубокого усвоения знаний, необходимых для профессиональной деятельности инженера, приобрести умение прогнозировать явления, происходящие в изучаемых технических объектах, учит основам конструирования новых технических устройств с заданными функциональными свойствами.
Рецензенты:
Шамало Т.Н., д.п.н., профессор, проректор по учебной работе УрГПУ, ФГБОУ ВПО Уральский государственный педагогический университет, г. Екатеринбург.
Усольцев А.П., д.п.н., профессор, заведующий кафедрой Теории и методики обучения физике, технологии и мультимедийной дидактики, ФГБОУ ВПО Уральский государственный педагогический университет, г. Екатеринбург.



