Введение
Особенностью таких промышленных производств, как электролиз алюминия, цинка, водорода и т.п., является использование электроприемниками энергии постоянного тока значительной мощности при одновременной необходимости плавного регулирования ее параметров. Плавное регулирование достигается применением управляемых мощных выпрямительных агрегатов, в которых управление электрическим режимом осуществляется изменением угла управления (тиристорное или дроссельное управление). Однако данный способ отличается уменьшением коэффициента мощности преобразовательного агрегата, значение которого может достигать недопустимых величин. Возможные пути решения указанной проблемы описаны в патентах [3; 4]. Эти пути решения являются, по сути, применением принципа векторного управления, используемого в гибких линиях электропередач переменного тока [2], к мощным вентильным преобразователям. С целью обеспечения практического применения указанных способов необходимо произвести исследование протекающих в таких выпрямительных агрегатах электромагнитных процессов.
Материалы и методы исследования
В настоящей работе проведено исследование квазиустановившихся электромагнитных процессов, протекающих в компенсированном выпрямительном агрегате с векторным управлением. Расчет проведен в соответствии со вторым уровнем абстракций [5] (расчет численно-аналитическим методом, построенным на согласовании решений, полученных для интервалов постоянной структуры, при использовании обычных для мощных выпрямительных агрегатов допущений). В целях упрощения изложения материала и в силу возможности дальнейшего обобщения полученных результатов на многофазные схемы исследование проведено на примере двухфазного компенсированного выпрямителя, схема которого показана на рис. 1. Источник ![]() – ЭДС питающей сети, источник
– ЭДС питающей сети, источник ![]() соответствует выходному напряжению автономного инвертора с ШИМ, пропущенному через низкочастотный фильтр (учитывается его первая гармоника). Источник тока Idy учитывает обмен активной мощности между звеном управления (автономный инвертор с входным и выходным фильтрами) и шинами постоянного тока (для выпрямителя, описанного в [4] Idy=0).
соответствует выходному напряжению автономного инвертора с ШИМ, пропущенному через низкочастотный фильтр (учитывается его первая гармоника). Источник тока Idy учитывает обмен активной мощности между звеном управления (автономный инвертор с входным и выходным фильтрами) и шинами постоянного тока (для выпрямителя, описанного в [4] Idy=0).
Для схемы, показанной на рис. 1, система уравнений для всех интервалов постоянной структуры имеет вид:
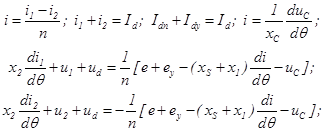 (1)
(1)
где ![]() – коэффициент трансформации;
– коэффициент трансформации;
![]() – сопротивление сети, сопротивления рассеяния первичной и вторичных обмоток трансформатора, сопротивление конденсатора соответственно на основной гармонике.
– сопротивление сети, сопротивления рассеяния первичной и вторичных обмоток трансформатора, сопротивление конденсатора соответственно на основной гармонике.
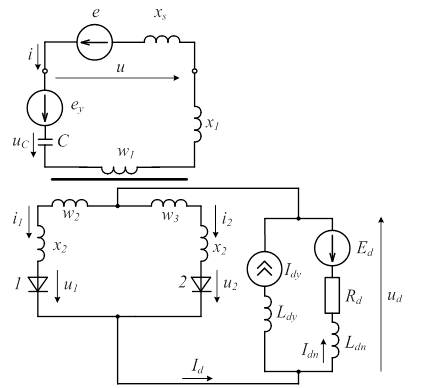
Рис. 1. Схема компенсированного выпрямителя с векторным управлением.
Для внекоммутационного интервала ![]() , связанного с работой вентиля 2, решение системы уравнений (1) имеет вид:
, связанного с работой вентиля 2, решение системы уравнений (1) имеет вид:
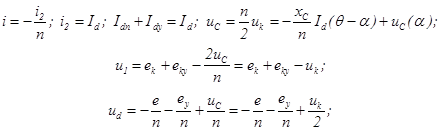 (2)
(2)
где ![]() – коммутирующая ЭДС питающей сети;
– коммутирующая ЭДС питающей сети;
![]() – коммутирующая ЭДС управления;
– коммутирующая ЭДС управления;
![]() – напряжение конденсатора, трансформируемое в контур коммутации (напряжение коммутации). Здесь и далее угол управления
– напряжение конденсатора, трансформируемое в контур коммутации (напряжение коммутации). Здесь и далее угол управления ![]() отсчитывается от момента перехода коммутирующей ЭДС сети
отсчитывается от момента перехода коммутирующей ЭДС сети ![]() через ноль.
через ноль.
Для коммутационного интервала ![]() , преобразуя (1) с учетом
, преобразуя (1) с учетом ![]() , приходим к следующей системе уравнений:
, приходим к следующей системе уравнений:
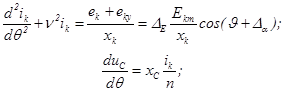 (3)
(3)
где ![]() – ток коммутации;
– ток коммутации;
![]() – сопротивление контура коммутации;
– сопротивление контура коммутации;
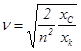 – относительная собственная частота контура коммутации;
– относительная собственная частота контура коммутации;
![]() – коэффициенты, учитывающие отличие суммарной коммутирующей ЭДС
– коэффициенты, учитывающие отличие суммарной коммутирующей ЭДС ![]() от коммутирующей ЭДС сети
от коммутирующей ЭДС сети ![]() соответственно по амплитуде и по фазе.
соответственно по амплитуде и по фазе.
Общее решение системы ДУ (3) имеет следующий вид:
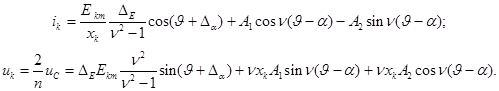 (4)
(4)
Граничные условия по концам интервала коммутации ![]() :
:
![]() . (5)
. (5)
Используя граничные условия (5), получим выражения для ![]() с учетом базисного значения тока
с учетом базисного значения тока ![]() для данной схемы:
для данной схемы:
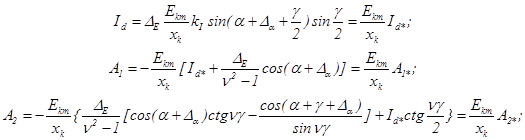 (6)
(6)
где 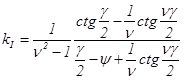 ;
;
![]() – схемный параметр рассматриваемого двухфазного преобразователя.
– схемный параметр рассматриваемого двухфазного преобразователя.
Токи вентилей для любого интервала постоянной структуры находятся по формулам:
![]() (7)
(7)
Напряжение коммутации во внекоммутационном интервале:
![]() (8)
(8)
В том же интервале выпрямленное напряжение:
![]() (9)
(9)
Напряжение на вентиле 1 в течение внекоммутационного интервала:
![]() (10)
(10)
Напряжение в точке подключения преобразователя к питающей сети при ![]() :
:
![]() (11)
(11)
Из условия ![]() получим выражение для угла управления
получим выражение для угла управления ![]() :
:
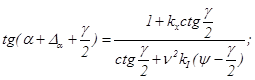 (12)
(12)
где ![]() .
.
Для коммутационного интервала соблюдаются следующие соотношения:
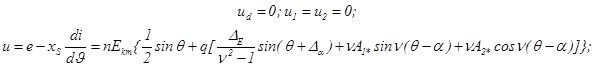 (13)
(13)
где ![]() – доля приведенного сопротивления питающей сети в сопротивлении контура коммутации.
– доля приведенного сопротивления питающей сети в сопротивлении контура коммутации.
С использованием условий периодичности, непрерывности и симметрии находятся токи и напряжения исследуемого преобразователя во внекоммутационном ![]() и коммутационном
и коммутационном ![]() интервалах. С учетом всего вышесказанного, среднее значение выпрямленного напряжения находится по формуле:
интервалах. С учетом всего вышесказанного, среднее значение выпрямленного напряжения находится по формуле:
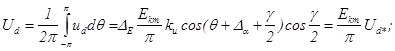 (14)
(14)
где ![]()
![]() – величина выпрямленного напряжения, нормированная по базисному напряжению
– величина выпрямленного напряжения, нормированная по базисному напряжению ![]() .
.
Результаты и их обсуждение
Выражения, подобные (4) – (14), были описаны для компенсированного преобразователя без векторного управления в [5]. Обобщение результатов для случая преобразователя с векторным управлением приводит к появлению в этих выражениях дополнительного множителя ![]() и дополнительного слагаемого аргумента тригонометрических функций
и дополнительного слагаемого аргумента тригонометрических функций ![]() . Множитель
. Множитель ![]() показывает возможность регулирования режима работы нагрузки, а слагаемое
показывает возможность регулирования режима работы нагрузки, а слагаемое ![]() – сдвиг момента переключения вентилей относительно напряжения сети.
– сдвиг момента переключения вентилей относительно напряжения сети.
По полученным выше соотношениям на рис. 2 построены временные диаграммы. Диаграммы построены при следующие условиях: ![]()
![]() .
.
Временные зависимости нормированы, для наглядности помножены на представленные на рисунке соответствующие коэффициенты. Показанные зависимости подтверждают описанную в [3; 4] возможность плавного регулирования выпрямленного напряжения без уменьшения коэффициента мощности (![]() ). Регулирование может производиться как с увеличением (
). Регулирование может производиться как с увеличением (![]() ), так и с уменьшением (
), так и с уменьшением (![]() ) выпрямленного напряжения. Угол управления
) выпрямленного напряжения. Угол управления ![]() зависит как от суммарной коммутирующей ЭДС
зависит как от суммарной коммутирующей ЭДС ![]() , так и от коммутирующего напряжения
, так и от коммутирующего напряжения ![]() . Как и в традиционном компенсированном выпрямителе, наличие коммутирующего напряжения
. Как и в традиционном компенсированном выпрямителе, наличие коммутирующего напряжения ![]() в контуре коммутации позволяет производить компенсацию реактивной мощности за счет опережающей искусственной коммутации вентилей (
в контуре коммутации позволяет производить компенсацию реактивной мощности за счет опережающей искусственной коммутации вентилей (![]() ) [1]. Возможность изменения фазы управляющего напряжения
) [1]. Возможность изменения фазы управляющего напряжения ![]() открывает путь к осуществлению дополнительной компенсации реактивной мощности за счет сдвига момента перехода суммарной коммутирующей
открывает путь к осуществлению дополнительной компенсации реактивной мощности за счет сдвига момента перехода суммарной коммутирующей ![]() в сторону опережения относительно того же момента у коммутирующей ЭДС сети
в сторону опережения относительно того же момента у коммутирующей ЭДС сети ![]() . Определение оптимального в том или ином смысле сочетания указанных двух способов компенсации реактивной мощности в компенсированном преобразователе с векторным управлением является предметом дальнейшего исследования. Результаты исследования должны быть обобщены на многофазные схемы.
. Определение оптимального в том или ином смысле сочетания указанных двух способов компенсации реактивной мощности в компенсированном преобразователе с векторным управлением является предметом дальнейшего исследования. Результаты исследования должны быть обобщены на многофазные схемы.
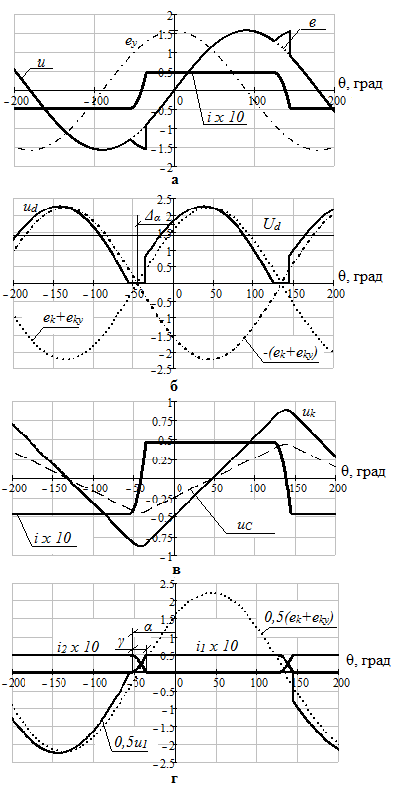
Рис. 2. Временные диаграммы токов и напряжений двухфазного нулевого компенсированного выпрямителя с векторным управлением:
а – ЭДС, напряжение и ток сети, ЭДС управления; б – выпрямленное напряжение, ЭДС коммутации; в – напряжения коммутации и на конденсаторе, ток конденсатора; г – токи вентилей, напряжение вентиля.
Выводы
-
Представлена теория квазиустановившихся электромагнитных процессов в двухфазном компенсированном выпрямителе, обобщенная для случая векторного управления.
-
На основе описанной теории построены временные диаграммы токов и напряжений выпрямителя, достоверность которых подтверждена математическим моделированием в среде MATLAB Simulink.
-
Временные диаграммы подтверждают возможность плавного регулирования выпрямленного напряжения без уменьшения коэффициента мощности.
-
Компенсация реактивной мощности осуществляется опережающей искусственной коммутацией вентилей, обеспечиваемой как напряжением на коммутирующем конденсаторе, так и опережающим сдвигом суммарной коммутирующей ЭДС относительно момента естественного перехода коммутирующей ЭДС питающей сети через ноль.
Рецензенты:
Ганджа С.А., д.т.н., профессор, заведующий кафедрой «Теоретические основы электротехники» ФГБОУ ВПО Южно-Уральский государственный университет (НИУ), г.Челябинск.
Воронин С.Г., д.т.н., профессор, заведующий кафедрой «Электромеханика и электромеханические системы» ФГБОУ ВПО Южно-Уральский государственный университет (НИУ), г. Челябинск.



