Введение
При системном исследовании химического обогащения железных руд [1–8] обнаружено не характерное для гетерогенных процессов явление, которое заключается в следующем. При выщелачивании кремния из рядового Криворожского концентрата растворами гидроксида натрия при температурах от 80 до 125 °С (этот температурный интервал находится ниже температур кипения соответствующих растворов щёлочи, поэтому давление насыщенного пара растворов не превышает атмосферного давления) лимитирующей стадией процесса является диффузия и энергия активации равна 23 кДж/моль. Но если выщелачивание проводится при более высоких температурах (выше температур кипения растворов щёлочи), то диффузионное торможение снимается и лимитирующей стадией становится скорость химических реакций. При этом энергия активации равна 76,5 кДж/моль [2].
Возникает задача наблюдать этот переход в одном опыте, и автоклавные процессы, широко используемые в химической технологии и гидрометаллургии, предоставляют такую возможность. В промышленных автоклавах периодичного действия процессы протекают при постоянном повышении температуры от комнатной до заданного «рабочего» значения. Если нагрев осуществляется с постоянной скоростью (линейный нагрев) и по ходу нагрева контролируется степень выщелачивания, то результаты таких исследований можно использовать для описания кинетики процесса и вычисления энергии активации. Но для описания таких процессов необходимо соответствующее кинетическое уравнение.
Вывод кинетического уравнения
Кинетическое уравнение первого порядка, которым описывается гетерогенный процесс выщелачивания кремния из рядового концентрата, в дифференциальной форме имеет вид:
![]() ,
,
где С – концентрация вещества к моменту времени t (в данном случае это концентрация кремния в руде, который к этому моменту времени ещё не извлечён в раствор);
k – константа скорости реакции;
Т – температура;
A – предэкспоненциальный множитель;
Eа – энергия активации.
Линейность нагрева выражается уравнениями:
![]() или
или ![]()
где ![]() – скорость нагрева (постоянная величина).
– скорость нагрева (постоянная величина).
Подставляя значение ![]() в дифференциальное кинетическое уравнение первого порядка, получаем:
в дифференциальное кинетическое уравнение первого порядка, получаем:
![]()
Для перехода к интегральной форме левая часть интегрируется от Cо (максимальная концентрация кремния в руде до начала выщелачивания) до С (концентрация при температуре отбора пробы), а правая от 0 до Т. Результатом является интегральное уравнение:
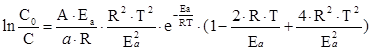
В левой части этого уравнения проводим следующие преобразования:
1) переходим от натурального логарифма к десятичному;
2) принимаем С0 равным единице (С0 = 1), тогда С = 1 – a, где a – степень выщелачивания кремния в долях от единицы.
В правой части проводим сокращение одинаковых величин в числителе и знаменателе. После этих преобразований имеем:
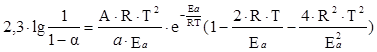
Разделив левую и правую часть полученного уравнения на Т2 и прологарифмировав, получаем конечное уравнение:
![]()
При вероятных значениях энергии активации, известных по результатам обработки опытных данных, полученных при выщелачивании при постоянных температурах [2], выражение в скобках в правой части уравнения почти не отличается от единицы:
![]()
Поэтому первый член в правой части конечного уравнения является постоянной величиной.
Следовательно, выведенное уравнение является линейным, и экспериментальные результаты должны укладываться на прямую линию в координатах:
![]() ¾
¾ ![]()
По наклону этой прямой можно вычислить энергию активации, так как тангенс её наклона равен энергии активации, поделённой на произведение R·T.
Результаты математической обработки
В табл. 1 приведены экспериментальные данные по выщелачиванию кремния при линейном нагревании автоклава и результаты их математической обработки по выведенному уравнению. Прямолинейность экспериментальных результатов в указанных координатах подтверждается графиком на рис. 1.
Таблица 1
Экспериментальные данные по выщелачиванию кремния 25 %-м раствором гидроксида натрия при линейном нагревании автоклава до 180 °С
и результаты их математической обработки
|
Время t, мин. |
Температура
|
|
Степень выщелачивания кремния a, % |
|
|
|
°С |
К |
||||
|
30 60 90 105 120 135 150 180 195 210 |
45 70 94 105 119 133 145 163 173 180 |
318 343 367 378 392 406 418 435 446 453 |
– – 2,72 2,65 2,55 2,46 2,39 2,29 2,24 2,21 |
– – 16,8 20,6 24,4 30,3 43,9 90,0 97,5 99,5 |
– – 0,117 0,223 0,260 0,340 0,52 1,083 1,267 1,410 |
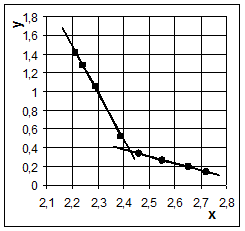
Рис. 1. Экспериментальные данные по выщелачиванию кремния при линейном нагревании автоклава до 180 °С в координатах:
![]() (х) ¾
(х) ¾ 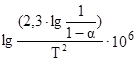 (y)
(y)
Из рисунка видно, что график фактически состоит из двух прямых линий, проходящих под разными углами, пересечение которых происходит при температуре около 140 °С. При низких температурах (ниже 140 °С, правая часть графика) энергия активации равна
19 кДж/моль, что близко к значению, полученному в опытах при атмосферном давлении (22,8 кДж/моль). При температурах выше 140 °С (левая часть графика) энергия активации равна 86 кДж/моль, что близко к значению Еа (76,5 кДж/моль), полученному в опытах при изотермическом автоклавном выщелачивании.
Наиболее вероятными причинами перехода режима выщелачивания из диффузионной области в кинетическую являются разрыхление частиц исходного обрабатываемого концентрата и уменьшение вязкости раствора.
Главной причиной снятия диффузного торможения мы считаем разрыхление частиц руды, появление в них пористости вследствие выщелачивания примесей. Свидетельством появления пористости является увеличение удельной поверхности руды после автоклавного выщелачивания на 35–40 %, тогда как при выщелачивании при атмосферном давлении она увеличивается на 15–20 %. Другой вероятной причиной снятия диффузионного торможения может быть уменьшение вязкости раствора, которая для 20 %-го раствора гидроксида натрия при 180 °С в 20 раз меньше, чем при 20 °С.
Таким образом, математическая обработка экспериментальных результатов, полученных при линейном нагревании автоклава, однозначно свидетельствует о переходе процесса выщелачивания из диффузионной области в кинетическую при температуре около 140 °С
и подтверждает эффективность автоклавного выщелачивания вследствие этого перехода.
Выводы
- Предложено уравнение для математического описания процесса выщелачивания при линейном нагревании автоклава с постоянной скоростью повышения температуры и проведена кинетическая обработка соответствующих опытных данных.
- Установлено ранее неизвестное явление перехода процесса выщелачивания из диффузионного режима в кинетический при температуре около 140 °С и эффективность автоклавного выщелачивания вследствие этого перехода.
Рецензенты:
Саркисов Ю.С., д.т.н., профессор, заведующий кафедрой химии Томского государственного архитектурно-строительного университета, г. Томск.
Лотов В.А., д.т.н., профессор кафедры силикатов и наноматериалов Томского политехнического университета, г. Томск.



