Введение
Совершенствование методов управления производством и повышение его эффективности является проблемой, которая никогда не теряет своей актуальности. Одним из главных инструментов этой проблемы, на современном этапе, является компьютерное моделирование и имитационный анализ организационно-экономических процессов с целью выяснения динамики развития производства. Учитывая огромное количество работ, посвященных различным аспектам моделирования и анализа производственных процессов, не считаем для себя возможным проведение адекватного обзора существующей современной литературы. Поэтому отметим лишь основополагающие труды, изложенные во второй половине прошлого века в монографиях [2,6,7]. В работе [6] организация рассматривается в качестве самонастраивающейся системы динамического характера. В [7] предлагается метод моделирования предприятия как динамического экономического объекта в рамках информационной взаимосвязи между этапами производственного процесса. В [2] развивается так называемый «арифметический менеджмент» с широким использованием математики и системного подхода к решению проблем управления. Имитационные модели анализа организационно-экономических процессов с целью выяснения динамики их развития были разработаны в [1, 10]. В предлагаемой нами статье принципы построения уравнений материальных и информационных потоков, заложенные в указанных выше трудах, обобщены для современных логистических систем, характеризуемых случайностью, неопределенностью и возмущенностью их основных параметров и показателей.
Объект исследования
Целью данной работы является разработка методов моделирования, анализа и принятия решений на основе типовых логистических модулей. Каждая из этих модулей предназначена для достижения определенных целей – от анализа влияния отдельных показателей на эффективность производственного процесса до получения траектории динамики развития производственной системы. На рис.1 приведена общая схема объекта исследования, состоящая из производства со своим складом и звена сбыта, также имеющего свой склад.
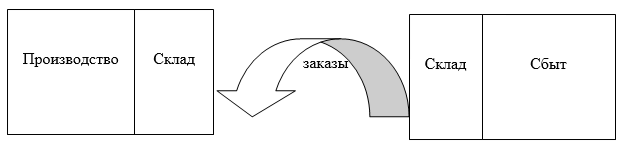
Рисунок 1. Объект исследования
В данной работе ограничимся только звеном сбыта, т.е. производство пока будет играть пассивную роль оптовой базы поставщика товаров. Рассмотрим несколько типовых логистических схем функционирования объекта исследования. Первая схема приведена на рис. 2 и предназначена для анализа влияния отдельных параметров системы на ее эффективность.
Рисунок 2. Логистическая схема функционирования объекта исследования
В блоке «Потребление» формируется случайный поток требований {t, S}, где t – моменты поступления требований, а S – значение спроса. В блоках «Складирование» и «Поставка» соответственно осуществляются хранение и организация поставок на склад.
Основными параметрами данной системы являются величина (случайная) спроса S, критическая величина товара на складе Vcr, стратегия определения величины поставок из оптовой базы, основанная на выборе параметра
.
Вторая схема приведена на рисунке 3 и характеризует динамику функционирования звена сбыта логистической системы. Принципиальным отличием этой схемы от первой является не только учет объемных параметров, но и интенсивностей материальных и информационных потоков системы и влияния на эти интенсивности фактора запаздывания.
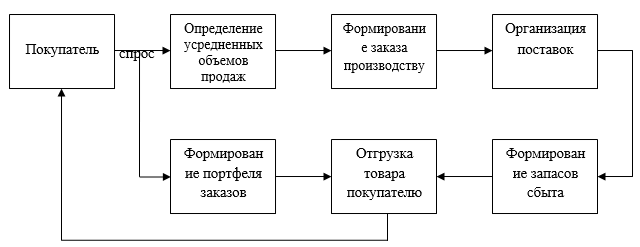
Рисунок 3. Функциональная структура
Технологические схемы модулей
Исходя из цели первого модуля, заключающегося в анализе влияния его основных параметров на эффективность процессов, построим следующую технологическую схему функционирования системы (рис. 4).
Из этого рисунка можно наглядно представить значение и суть большинства параметров системы. Функционирование модуля начинается с моделирования потока требований (спроса) потребителей. Средний спрос Sm, определяемый в блоке 2 для фиксированных моментов времени (начало месяца, декады или недели), является основой для планирования объемов поставок. Параметры СХ, СР, СD являются интегральными значениями, соответственно, затрат на хранение товара, организацию поставок и издержек дефицита товара. Параметр 
характеризует длительность организации поставок.
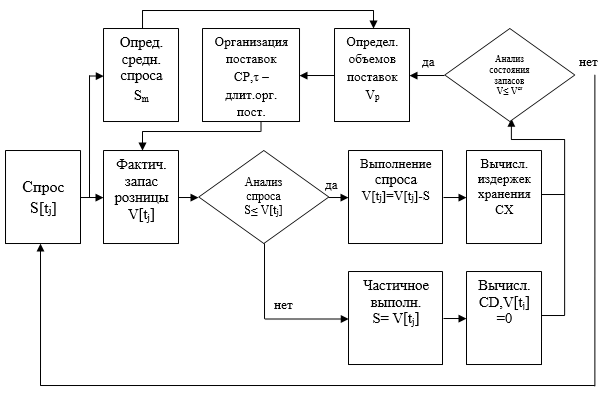
Рисунок 4. Технологическая схема модуля 1
Построим технологическую схему функционирования второго модуля (рис. 5) на основе принципа «проточного резервуара». Этот принцип впервые использован Дж. Форрестeром [7] и предполагает чередование блоков, характеризующих показатели объемов с показателями интенсивностей потоков. Действительно, величины объемов получаются как разница между входной и выходной интенсивностями блоков.
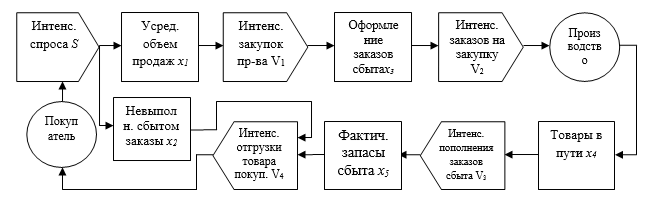
Рисунок 5. Технологическая схема модуля 2
Уравнения процессов
Опишем уравнения процессов, протекающих в технологической схеме, приведенной на рис.5. Так как в блоке «интенсивность спроса» формируется внешний поток спроса, начнем с описания процессов блока «усредненный объем продаж». Усредненное значение спроса (или интенсивности продаж) является важным параметром системы, на который основываются планы по формированию запасов товара на складе и объемы заказов для восполнения этих запасов. Усредненное значение продаж 
, где
– текущий момент времени, получается как предшествующее значение усредненных продаж в момент времени
, скорректированное на некоторую долю разности между интенсивностью продаж в течение последнего интервала времени
и рассчитанным ранее средним значением продаж 
, где 
. (1)
Здесь константа a1 является долей разности, на которую необходимо корректировать интенсивность продаж товаров.
Интенсивность закупок от поставщиков 
от до 
, в последующем интервале определяется уравнением (2)
, (2)
Смысл этого уравнения также достаточно прозрачен. Очевидно, интенсивность розничных закупок будет в первую очередь зависеть от сложившейся интенсивности продаждля восполнения запаса взамен проданных. Вторая часть уравнения является корректировкой сложившейся интенсивности в зависимости от разности между желательным 
и фактическими
запасами с учетом запаздывания a2 реакции системы на возникновение дефицита товаров в запасе. Здесь a3 – коэффициент пропорциональности между усредненным значением продаж и желательным запасом сбыта.
Величина заказов звена сбыта
, которые находятся на стадии оформления, определяется из уравнения (3)
(3)
В соответствии с принципом «проточного резервуара» переменная
является выданной звеном сбыта интенсивностью закупок товаров и определяется уравнением (4)
(4)
где a2 – запаздывание оформления заказа в звене сбыта.
Организация поставок товара в звене сбыта, отраженные в блоках «товары в пути» и «интенсивность пополнения запасов», описываются уравнениями (5) и (6) и имеют аналогично с (3) и (4) структуру построения
, (5)
(6)
Здесь a4 – запаздывание транспортировки товаров в звене сбыта.
V3 – поставки, получаемые звеном сбыта.
W1 – поставки, осуществляемые со склада производства.
Аналогично можно получить и уравнение, определяющее фактические запасы сбыта x5 и величину невыполненных сбытом требований x2
(7)
(8)
А для интенсивности отгрузки товара потребителям 
получим выражение
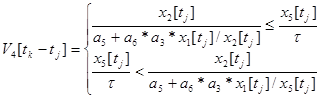, (9)
где a5 – минимальное запаздывание выполнения заказа звеном сбыта; a6 – запаздывание выполнения заказов организационного характера.
Значение интенсивности V4 равняется левой части того неравенства, которое справедливо в конкретном случае.
Алгоритм процесса функционирования звена сбыта
Начнем с подалгоритма моделирования потока
. Моделирование моментов поступлений требований {tj}рассмотрим для достаточно общего случая, когда множество 
образует стационарный поток Пальма с заданной функцией плотности j(t) интервалов между элементами, начиная со второго интервала потока Т. Для определения моментов tj воспользуемся стандартной формулой 
, j = 1, 2, …, n,где 
– интервалы между элементами цепи Т.
Для моделирования потоков Пальма недостаточно знание j(t), так как функция плотности первого интервала обычно отличается от j(t), т.е. j1(t) ¹j(t).
Поэтому для определения j1(t) надо воспользоваться формулой Пальма
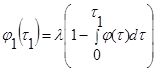, (8)
где l – интенсивность потока.
Значения интервалов tj между элементами цепи Т определяются методом обратной функции моделирования непрерывных случайных величин, принцип которого формулируется в виде теоремы: «Случайная величина t, реализации которой определяются из выражения
или 
, (9)
где u – случайная величина, равномерно распределенная на отрезке [0, 1], имеет плотность распределения j(t)» или основным методом моделирования дискретных величин, основанным на теореме: «Величина tk, заданная в виде таблицы
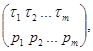
наступает с вероятностью pk при выполнении условия uÎDk, где Dk= pk»[3].
В качестве базовой случайной величины x рассматривается случайная величина, равномерно распределенная в интервале [0, 1]. Доказательства данных теорем можно найти в [8].
Если функция плотности j(t) интервалов между элементами потока Т является непрерывной случайной величиной и подчиняется одному из известных теоретических законов распределения, то для моделирования значений интервалов tj между элементами цепи Т можно воспользоваться формулами, приведенными, например в [8].
С учетом вышесказанного подалгоритм «Спрос» моделирования требований потребителей состоит из 4 шагов.
Шаг 1. Определение по формуле Пальма (8) функции плотности j1(t1).
Шаг 2. Используя формулы (9) определение зависимостей
и 
, j> 1
и вычисление интервалов между моментами поступления требований.
Шаг 3. Вычисление по формулеэлементов цепи {tj}.
Шаг 4. Используя метод обратной функции определение зависимости
для нахождения значений требований потребителей в момент времени.
Перейдем к построению алгоритма функционирования технологической схемы первого модуля (рис. 4).
Шаг 1. Моделирование потока требований 
с помощью подалгоритма «Спрос».
Шаг 2а. Вычисление среднего спроса
.
Шаг 2б. Вычисление фактического запаса на складе 
.
Шаг 3. Проверка возможности удовлетворения спроса. Если уровень запаса больше спроса – переход на шаг 4, если меньше спроса – переход на шаг 6.
Шаг 4. Уменьшение уровня запасов на объем спроса
.
Шаг 5. Вычисление затрат на хранение товаров
. Затраты на хранение включают арендную плату за склад, страховки, расходы на обслуживание и налоги и т.д.
Шаг 6. В случае, когда уровень запаса меньше спроса, оформление заказа на соответствующее количество товара.
Шаг 7. Вычисление издержки дефицита товара
. Это издержки, связанные с неудовлетворенным спросом, возникающим в результате отсутствия товара на складе.
Шаг 8. Проверка состояний запасов
. Если нет, то переход на шаг 1.
Шаг 9. Вычисление объема поставокVp.
Шаг 10. Вычисление затрат на организацию поставок 
. Это затраты, связанные с организацией заказа и его реализацией и доставкой товаров на склад. Переход на шаг 2б.
Рассмотренный алгоритм описывает систему управления запасами с фиксированным интервалом времени между заказами. Реализация текущего запаса в общем случае представляет собой случайный дискретный процесс, отражающий нестационарность и стохастичность спроса. Момент окончания каждой реализации случаен, но в одних случаях остаточный запас в момент поставки больше нуля, в других – равен нулю. Спрос на товары удовлетворяется за счет имеющегося запаса. Критический запас создается для защиты от возможного дефицита в случаях, когда реальный спрос оказывается больше, чем прогнозируемый, или, если время, необходимое для пополнения запаса, превышает прогнозируемое.
Перейдем к построению алгоритма функционирования технологической схемы второго модуля (рис.5).
Шаг 1. Моделирование по методу обратной функции интенсивности спроса покупателя S, которая является случайной величиной с известным распределением.
Шаг 2а. Определение усредненного объема продажпо формуле (1).Усреднение, в основе которого лежит зависимость, описываемая показательной функцией, дает наиболее весомый результат в том случае, когда оно охватывает данные, полученные в самое последнее время. Переход на шаг 3.
Шаг 2б. Вычисление невыполненных сбытом заказов
. Переход на шаг 10.
Шаг 3. Вычисление интенсивности выдачи исходящих заказав
.
Шаг 4. Вычисление величины заказов в звене сбыта, находящиеся на стадии оформления.
Шаг 5. Вычисление интенсивности заказов на закупку товаров, выданной звеном сбыта.
Шаг 6. Вычисление количество товаров, находящиеся в пути к звену сбыта
, которая отображает транспортировку товаров из производства в звено сбыта.
Шаг 7. Определение интенсивности поставок, пополнившие запасы в звене сбыта
.
Шаг 8. Вычисление величины фактического запаса в звене сбыта
.
Шаг 9. Определение интенсивности отгрузки товара покупателю.
Интенсивности потоков отражают активность, в то время как объемы измеряют состояние, которое является результатом активности в системе. Уравнения интенсивности регулируют действия, которые должны произойти в системе за следующий интервал времени. Уравнения интенсивности, как и уравнения объемов, на протяжении каждого интервала времени решаются независимо одно от другого.
Заключение и перспектива развития исследований
В статье предложена технологическая схема сбытовой системы с учетом случайности, неопределенности и возмущенности ее основных параметров и показателей. Описаны уравнения материальных и информационных потоков для исследования процессов управления и функционирования производственно-сбытовых систем. Также разработаны алгоритмы процессов функционирования предложенных модулей звена сбыта. Эти алгоритмы характеризуются простотой, эффективностью и отсутствием избыточности. Мы считаем, что эти технологические схемы модулей являются универсальными и актуальны не только для объекта исследования обсуждаемого в этой статье, но и для описания более сложной, составной схемы многомодульных логистических цепей.
Будущие исследования должны расширить систему сбыта для определенной предметной области. Как показывает анализ ряда современных работ в области логистических систем [4, 5, 9], это потребует обработку сложных многоступенчатых движений с многочисленными поставщиками услуг и видов транспорта. Кроме того, технологические схемы функционирования системы сбыта нуждаются в дальнейшем улучшении. В перспективе, рассмотренный подход имитационного моделирования системы сбыта должен быть объединен с системой производства, обеспечивая тем самым полную основу для построения имитационных моделей реальных производственно-сбытовых систем и совершенствования процессов их функционирования. Также полученные в работе имитационно-аналитические модели типовых модулей являются основой для создания информационной системы анализа и планирования процессов в логистических системах.
Рецензенты:
Бияшев Р.Г., д.т.н., профессор, зам. директора по прикладным, рисковым и инициативным проектам. Заведующий лабораторией информационной безопасности, г. Алматы.
Джурунтаев Д.З., д.т.н., профессор кафедры «Информационная безопасность» Казахского национального технического университета имени К.И. Сатпаева, г. Алматы.