Введение
Решение проблемы обеспечения надёжности широкого класса территориально распределенных обслуживаемых систем с применением передовых технологий эксплуатации, основанных на учете фактического технического состояния, связано с построением и поддержанием устойчивого функционирования систем сбора и обработки информации (ССОИ) о характеристиках эксплуатационных процессов [6]. Одной из ключевых характеристик ССОИ подобного назначения является готовность ССОИ, под которой понимается свойство системы оперативно восстанавливать свою работоспособность при отказах элементов. Показателем готовности является коэффициент готовности, вычисляемый как вероятность застать систему в работоспособном состоянии в любой произвольно взятый момент времени, за исключением интервалов времени, когда использование ССОИ (или некоторой ее части) по предназначению не предусмотрено. Оценивание показателей готовности элементов системы сбора и обработки информации требует разработки соответствующей методики [4].
Цель исследования
Необходимо разработать методику, которая позволяет при заданных: структуре ССОИ; алгоритмах её функционирования по назначению; стратегиях обслуживания с учётом параметров системы технической эксплуатации (СТЭ) и степени обеспеченности необходимыми для поддержания и восстановления работоспособности элементов ССОИ запасами произвести расчёт показателей готовности ССОИ.
Материал и методы исследования
Методическое обеспечение для расчёта показателей готовности и временных показателей ССОИ с учётом параметров СТЭ должно обеспечивать решение следующих задач [2]: описание структуры рассматриваемой обслуживаемой системы в виде графа и описание состава и типов элементов, составляющих рассматриваемую систему; определение интенсивностей потоков заявок на обслуживание с учётом интенсивностей отказов элементов и периодичностей проведения плановых мероприятий по поддержанию и восстановлению работоспособности элементов различных типов; описание структуры и состава обслуживающих (ремонтных) органов, а также распределения технических средств, обслуживаемых каждым органом СТЭ; определение средних интенсивностей обслуживания заявок (без учёта времени нахождения в очереди на обслуживание) в зависимости от алгоритмов функционирования обслуживающих органов; составление функций работоспособности рассматриваемой обслуживаемой системы; получение для каждой функции работоспособности с помощью одного из известных алгоритмов вероятностной функции в форме разделённых произведений; выделение сочетаний состояний элементов обслуживаемой системы, являющихся зависимыми через общую систему обслуживания, и расчёт стационарных вероятностей состояний для таких групп элементов с использованием математического аппарата сетей массового обслуживания; расчёт требуемых показателей готовности; обслуживаемой системы и её отдельных функциональных подсистем; расчёт среднего времени восстановления работоспособности элемента обслуживаемой сети; расчёт коэффициентов готовности отдельных элементов обслуживаемой системы.
Результаты исследования и их обсуждение
Приведем характеристику способов и результатов решения перечисленных выше задач.
Оборудование ССОИ может состоять из нескольких (Е) элементов, часть из которых являются основными, а остальные – резервными. Обозначим ЕО – количество основных элементов определённого типа, необходимых для обеспечения работоспособности ССОИ. Общее число элементов, находящихся в нагруженном режиме, обозначим ЕН. В качестве элементов рассматриваемой системы возможны четыре типа структур: без резервирования (Е = ЕН = ЕO); с ненагруженным резервом (Е > ЕН = ЕO); с нагруженным резервом (Е = ЕН > ЕO); с комбинированным (нагруженным и ненагруженным резервом (Е > ЕН > ЕO)).
Определение интенсивностей потоков заявок на обслуживание с учётом интенсивностей отказов элементов L и периодичностей проведения плановых мероприятий по поддержанию и восстановлению работоспособности элементов различных типов производится на основе обработки результатов опытной эксплуатации пилотного образца ССОИ, либо по результатам имитационного моделирования c учетом функционального состояния операторов ССОИ [1].
В основу описания структуры и состава обслуживающих (ремонтных) органов, а также распределения технических средств, обслуживаемых каждым органом СТЭ, положены следующие допущения. Элементы, обслуживаемые т-м органом (
), составляют множество хт ≤ х*, причём равенство может быть только в двух случаях: либо каждый элемент может быть обслужен из любого центра обслуживания, либо все средства системы обслуживаются силами единственного обслуживающего органа, т.е. имеет место полностью централизованное обслуживание.
Определение средних интенсивностей обслуживания заявок (без учёта времени нахождения в очереди на обслуживание) выполняется в зависимости от алгоритмов функционирования обслуживающих органов. Наличие в т-м ремонтном органе 
каналов обслуживания учитывается зависимостью интенсивности обслуживания от количества заявок 
:
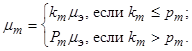. (1)
Величина mэ представляет собой интенсивность обслуживания заявок одним каналом обслуживания и определяется в зависимости от принятого в данной системе алгоритма работы [3]. Если обслуживание элементов осуществляется выездными бригадами, причём после удовлетворения заявки бригада возвращается обратно в центр обслуживания, то 
можно определить:
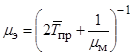, (2)
где 
– среднее время, затрачиваемое бригадой на передвижения между центром обслуживания и элементами системы; 
– среднее время, затрачиваемое бригадой на выполнение операций по обслуживанию. Если бригады действуют «автономно», то можно определить следующим образом:
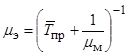, (3)
где – среднее по всем маршрутам между элементами системы время, затрачиваемое на передвижения.
В том случае когда, наоборот, средства, требующие обслуживания, доставляются в центр обслуживания (т.е. бригады не затрачивают времени на передвижения), то º 
.
Функция работоспособности ССОИ записывается в соответствии с заданным критерием работоспособности системы в общем случае в дизъюнктивной нормальной форме:
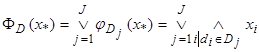, где 
– элемент системы, 
.
Для каждой функции работоспособности с помощью одного из известных алгоритмов [2] формируется вероятностная функция в форме разделённых произведений.
Выделение сочетаний состояний элементов обслуживаемой системы, являющихся зависимыми через общую систему обслуживания, и расчёт стационарных вероятностей состояний для таких групп элементов осуществляется с использованием математического аппарата сетей массового обслуживания. Расчёт стационарных вероятностей состояний сети массового обслуживания может быть произведён с учётом (1) – (3) с использованием выражения:
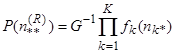. (4)
При этом подсистемы без резервирования, а также подсистемы, состоящие из элементов с нагруженным резервом, описываются системой массового обслуживания (СМО) типа IS (тип СМО, где число обслуживающих приборов не меньше суммарного количества заявок). Подсистемы с ненагруженным или комбинированным резервом описываются СМО с дисциплиной обслуживания FCFS («первый пришёл – первый обслуживается») и числом обслуживающих приборов, равным числу активно работающих элементов.
Процессы функционирования ремонтных органов наиболее точно отражает дисциплина обслуживания FCFSPR («первым пришёл – первым обслуживается с абсолютным приоритетом и дообслуживанием в случае прерывания»). Для расчёта таких СМО целесообразно использование имитационного моделирования [3]. Приоритеты заявок могут быть определены в зависимости от критичности отказа для функционирования средства и системы в целом.
Расчёт показателей готовности ССОИ и её отдельных функциональных подсистем выполняется следующим образом. Вероятность того, что в произвольный момент времени число технических средств данного типа, находящихся в работоспособном состоянии, окажется не менее предельно допустимого 
определяется для группы элементов с зависимыми состояниями через стационарные вероятности состояний СМО (4) как сумма вероятностей нахождения сети массового обслуживания во всех тех состояниях y, при которых условие п ≥ nдоп выполняется: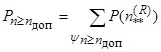 
.
Для функциональных подсистем, имеющих сетевую структуру, расчёт коэффициента готовности направления передачи информации 
может быть осуществлен с использованием выражения:
,
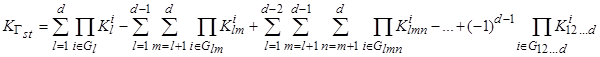где d – число простых путей в направлении передачи s – t; Glmn – множество номеров обслуживающих органов, в зоны обслуживания которых входят средства, составляющие l-й, т-й, п-й пути; 
– коэффициент одновременной готовности средств, входящих в l-й, т-й, n-й пути и обслуживаемых i-м органом обслуживания.
Среднее время наработки на отказ направления передачи 
при известных коэффициентах готовности элементов данного направления рассчитывается с использованием выражения
,
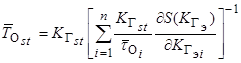где 
– среднее время наработки на отказ i-го элемента; 
– коэффициент готовности i-го элемента.
Расчёт среднего времени восстановления работоспособности элемента обслуживаемой сети 
производится с учётом того, что суммарное время восстановления складывается из времени, затраченного собственно на операции восстановления работоспособности, и времени ожидания обслуживания по причине отсутствия свободных каналов обслуживания. При этом может быть применена формула:
,
где 
– средняя интенсивность входящего в СМО, имитирующую работу ремонтного органа, суммарного потока заявок; 
– среднее число средств, находящихся на обслуживании и ожидающих начала обслуживания в ремонтном органе;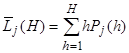 
, где Рj(h) – вероятность нахождения сети массового обслуживания в состояниях, когда в ремонтном органе и в очереди на обслуживание находится h заявок.
Расчёт коэффициентов готовности отдельных элементов CCОИ выполняется следующим образом. При двухуровневой структуре СТЭ коэффициент готовности может быть определен следующим выражением:
,
где 
, 
– средние времена восстановления работоспособности силами эксплуатирующего персонала (первый уровень ППВР) и силами специализированной ремонтной организации (второй уровень) соответственно; рН – вероятность того, что при отказе окажется в наличии в комплекте запасных элементов и принадлежностей (ЗИП) необходимый элемент замены и восстановление будет произведено силами эксплуатирующего персонала; (1 – рН) – вероятность того, что в ЗИП отсутствует необходимый элемент и восстановление работоспособности производится в специализированной ремонтной организации [5].
При трёхуровневой структуре СТЭ коэффициент готовности элемента может быть найден следующим образом:
,
где , , 
– средние времена восстановления работоспособности элемента силами соответствующих уровней СТЭ; рН1, рН2 – вероятность наличия необходимых для ремонта элементов замены на первом и втором уровнях СТЭ.
Заключение
В статье обсуждаются вопросы создания научно-методического аппарата для определения значений показателей готовности ССОИ. Под готовностью ССОИ понимается свойство системы оперативно восстанавливать свою работоспособность при отказах элементов. Показателями готовности является коэффициенты готовности, вычисляемые как вероятность застать систему (или некоторую ее часть) в работоспособном состоянии в любой произвольно взятый момент времени, за исключением интервалов времени, когда использование ССОИ (или некоторой ее части) по предназначению не предусмотрено. Оценивание показателей готовности элементов системы сбора и обработки информации потребовало разработки соответствующей методики, характеристика основных этапов которой приведена в настоящей статье.
Рецензенты:
Козлов В.В., д.т.н., профессор, профессор кафедры Военно-космической академии имени А.Ф. Можайского, г. Санкт-Петербург.
Садин Д.В., д.т.н., профессор, профессор кафедры Военно-космической академии имени А.Ф. Можайского, г. Санкт-Петербург.