Введение
В строительной отрасли существуют особые классы объектов, к ним относятся уникальные, опасные, технически сложные и другие аналогичные объекты. Как правило, при подготовке проектной документации продолжительность строительства таких объектов задается директивно заказчиком. Связано это с тем, что существующими нормативными документами [5; 7] продолжительность строительства таких объектов не регламентирована. После установки директивных сроков для подготовки организационно-технологической документации необходимо решить ресурсную задачу. Ресурсными называются задачи, в которых требуется определить количество трудовых и машинных ресурсов при известной общей продолжительности строительства и объемов работ [1]. Необходимость решения ресурсной задачи обусловлено МДС 12-46.2008 [6], согласно которому в проектной документации требуется предусмотреть условия и ресурсы для соблюдения директивной продолжительности строительства. При этом необходимо заметить, что в связи с заинтересованностью лиц, участвующих в инвестиционно-строительных проектах, в снижении затрат на реализацию проекта, подбор минимально необходимого количества трудовых ресурсов для завершения строительства точно в срок является важной задачей. Особо актуальной задача подбора необходимого количества рабочих становится при отсутствии данных о сметной стоимости строительства, что случается при проектировании коммерческих объектов. Связано это с тем, что, зная сметную стоимость и директивные сроки строительства, можно подобрать необходимое количество рабочих по средней выработке на одного рабочего в год. Но эти данные будут укрупненными и будут отсутствовать гарантии, что определено оптимальное количество трудовых ресурсов.
Цель исследования
В настоящее время для разработки календарных графиков существует ряд компьютерных программ, таких как Primavera [2], Open Plan [9], Microsoft Project [4] и др. Расчет календарных графиков в этих программах осуществляется методом критического пути, на основании введенных продолжительностей работ, и их очередностью, что в совокупности определяет организационно-технологическую схему производства работ. Подбор необходимого количества трудовых ресурсов для завершения строительства в директивные сроки осуществляется в режиме диалога исполнителя и компьютерной программы. При достаточной величине объекта и детализации календарного графика, что сопровождается большим количеством видов работ и захваток, такой метод подбора необходимого количества человеческих ресурсов становится весьма трудоемким, а в случае, когда директивные сроки установлены слишком сжатыми, вообще невозможным. Следует заметить, что такой метод определения необходимого количества трудовых ресурсов является эвристическим и не включает в себя математического обоснования. Это приводит к отсутствию гарантий нахождения наиболее оптимального количества трудовых ресурсов. Таким образом, возникает существенная необходимость в разработке алгоритма, позволяющего автоматизировать данный процесс и, используя математический аппарат, получить обоснованные результаты. В настоящей работе представляется укрупненный алгоритм решения ресурсной задачи, позволяющий автоматизировать этот процесс. Также в данном алгоритме используется математический аппарат, что позволяет получить обоснованные результаты.
Материал и метод исследования
Укрупненный алгоритм состоит из 3 этапов.
-
На первом этапе необходимо определить максимальное количество трудовых ресурсов, которые возможно привлечь, соблюдая требования техники безопасности при производстве строительно-монтажных работ, и рассчитать календарный график.
-
На втором этапе необходимо всю организационно-технологическую схему описать системой линейных уравнений. Таким образом, мы получим задачу линейного программирования и на следующем этапе решим ее симплекс-методом.
-
На третьем этапе производится оптимизационное уменьшение трудовых ресурсов путем решения полученной системы линейных уравнений методом линейного программирования.
Рассмотрим более подробно этапы, составляющие алгоритм.
На первом этапе определяется предельно возможное количество трудовых ресурсов для каждой захватки, которые необходимы для выполнения всех работ календарного плана. После их ввода программой управления проектами типа МР осуществляется расчет расписания работ методом критического пути. Использование в расчете максимального количества трудовых ресурсов позволяет получить минимально возможную продолжительность строительства. Затем сравниваются директивные сроки строительства со сроками при максимальном количестве ресурсов. Разница между этими сроками будет являться резервом времени, который можно использовать для оптимизационного уменьшения трудовых ресурсов. В результате применения оптимизационной процедуры плановая продолжительность должна сравняться с директивной продолжительностью при минимуме используемых ресурсов. Если же директивные сроки окажутся меньшими по сравнению со сроками при использовании максимального количества трудовых ресурсов, то в таком случае необходимо обоснованно увеличивать директивные сроки либо менять организационно-технологическую схему.
При проектировании календарного графика работы, входящие в него, необходимо будет привести к определенной иерархии. Иерархия будет представлять собой следующий вид.
-
На первом высшем уровне иерархии «работа – вид» – характеризующая соответственно вид выполняемой работы.
-
На втором уровне «работа – фронт» – характеризующая фронты каждого вида работ.
-
На третьем уровне «работа – ресурс» – характеризующая трудовые ресурсы, выполняющие определенный вид работы на определенном фронте работ.
Календарный график, фрагмент которого изображен на рисунке 1, построен с учетом описанной иерархии. Это требование обусловлено специфическими особенностями программного продукта MP, в котором на третьем этапе программируется алгоритм решения оптимизационной задачи линейного вида. В основе алгоритма лежит симплекс-метод.
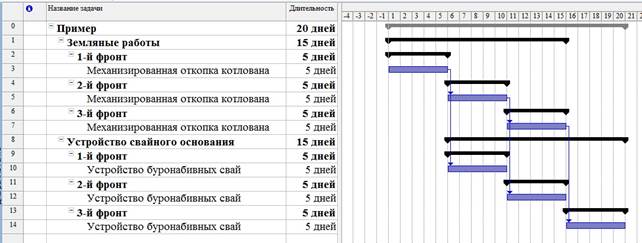
Рисунок 1. Фрагмент календарного графика в MP
Проиллюстрируем выполнение первого этапа на конкретном примере, а именно на объекте строительства многофункционального комплекса (МФК) «Лахта Центр». Для того чтобы определить организационно-технологическую схему производства работ МФК, разделить комплекс на захватки и определить предельно возможное количество рабочих для каждой захватки, необходимо ознакомиться с условиями и объектом строительства.
МФК «Лахта Центр» состоит из следующих объектов:
-
здание «Башня»;
-
многофункциональное здание (МФЗ), состоящее из северного и южного блоков и расположенного между ними крытого внутреннего двора (атриум);
-
стилобатная часть, состоящая из северной и южной площади, а также вестибюля главного входа в здание «Башня» в виде большепролетной арки.
Схема плана участка с расположением объектов комплекса отражена на рисунке 2.
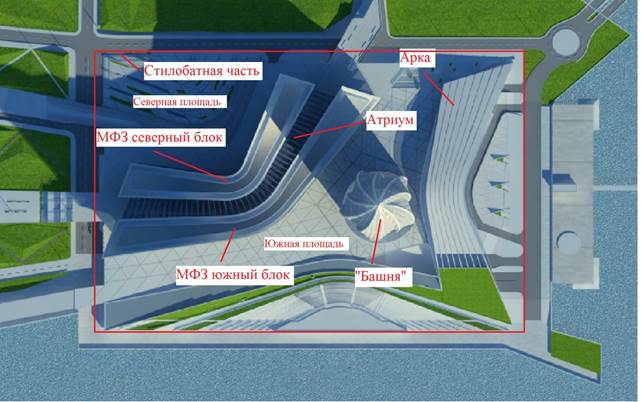
Рисунок 2. Генеральный план участка МФК «Лахта Центр»
Часть объектов, входящих в МФК, относится к категории уникальных. К уникальным объектам, в соответствии с Градостроительным кодексом [8], относятся объекты капитального строительства, в проектной документации которых предусмотрена хотя бы одна из следующих характеристик:
-
высота более чем 100 метров;
-
пролеты более чем 100 метров;
-
наличие консоли более чем 20 метров;
-
заглубление подземной части (полностью или частично) ниже планировочной отметки земли более чем на 15 метров.
В МФК уникальными являются:
-
здание «Башня», имеющее высоту 465 метров и заглубление подземной части на 18,6 метров;
-
МФЗ, имеющее вылет консольной части, равный 25 метрам.
Арка имеет пролет, равный 99 метрам. От внесения арки в категорию уникальных объектов не хватает увеличения длины пролета на два метра.
Уникальность объектов вызывает ряд трудностей при проектировании. Одной из таких трудностей является отсутствие нормативно-технической базы, которой можно руководствоваться при проектировании объектов. Так, например, в нормативно-технической литературе [5; 7] отсутствуют требования к нормативной продолжительности строительства здания «Башня», имеющего высоту 465 метров, большепролетной арки, МФЗ, а также стилобатной части. В связи с этим продолжительность строительства многофункционального комплекса (МФК) «Лахта Центр» была задана директивно и равнялась 1945 дням. Математическая обоснованность заданных сроков отсутствовала.
Объемно-планировочные решения многофункционального комплекса «Лахта центр» включают в себя здание «Башня» с развитой подземной частью, имеющей в своем основании форму правильного пятиугольника и прилегающей к нему со всех сторон двухуровневой стилобатной частью комплекса, которая в свою очередь включает в себя двухуровневую автостоянку, арку, а также многофункциональное здание.
В связи с тем что применение первого этапа укрупненного алгоритма в данной работе будет рассмотрено на примере возведения большепролетной арки, ограничимся описанием проектных решений только по этому зданию.
Арка, как отмечалось ранее, имеет пролет, равный 99 метрам. Основание арки свайное, ростверк – монолитная железобетонная плита. Арка состоит из одного подземного и одного надземного этажа. Каркас арки в уровне подземного и надземного этажей монолитный железобетонный и металлический. Из железобетона выполнены стены, перекрытия и опоры под фермы, а из металла конструкции покрытия арки.
Ознакомившись с условиями строительства, приступим к выполнению первого этапа укрупненного алгоритма решения ресурсной задачи. Определим предельное количество рабочих для возведения монолитного железобетонного каркаса здания арки.
Согласно [3] предельное число рабочих, которые могут работать на захватке, можно определить путем разделения фронта работ на делянки, размер которых должен быть равен сменной производительности звена или отдельного рабочего. Произведение числа делянок на состав звеньев дает максимальную численность бригады на данной захватке. Соответственно можно сделать вывод, что чем больше захватки, тем больше возможности сократить продолжительность строительства. При этом нельзя забывать, что сокращение продолжительности строительства имеет также ограничение по технологии производства работ и наличию рабочих.
Монолитный железобетонный каркас здания арки делится по ширине на две захватки. Связано это с тем, что здание арки длинной стороной прилегает к зданию «Башня», которое начинает возводиться в первую очередь. Разбив арку по ширине на две последовательно выполняемые захватки, мы обеспечим доступ к захватке техники с противоположной стороны от здания «Башня», что позволит совместить возведение этих зданий друг с другом, соблюдая при этом требования техники безопасности. По высоте арка делится на захватки по этажам. Один этаж – одна захватка. Так как в арке два этажа, соответственно по высоте всего две захватки. Разбивка на захватки каркаса здания арки в плане изображена на рисунке 3.
В связи с тем что устройство монолитных железобетонных конструкций нельзя выполнять за один день из-за технологических ограничений (необходимо время для набора бетоном прочности), принимаем: устройство монолитных железобетонных конструкций одной захватки 3 дня. Как было сказано выше, монолитный железобетонный каркас состоит из фундаментной плиты, стен и перекрытий. Таким образом, продолжительность выполнения в 3 дня будет относиться к каждому виду конструкций в отдельности, т.е. фундаментная плита – 3 дня, стены – 3 дня и перекрытие – 3 дня. Суммарное выполнение одной захватки подземного этажа будет равно 6 дням (фундаментная плита – 3 дня, стены и опоры – 3 дня), а одной захватки надземного этажа 3 дням, так как надземный этаж состоит только из плиты перекрытия и верха опор, на которых будут монтироваться металлические фермы.
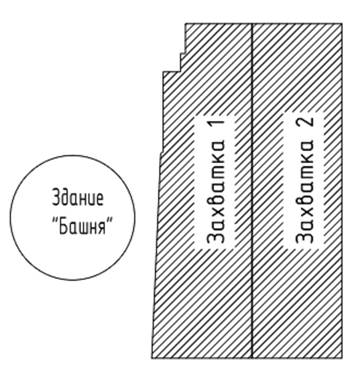
Рисунок 3. Разбивка на захватки каркаса здания арки
Далее определяется объем работ в одной захватке и трудоемкость вида работ по различным нормам. Нормативной базой могут служить:
-
ЕНиР (МНиР, ВНиР);
-
сметные нормативы (ТЕР, ГЭСН);
-
укрупненные комплексные нормативы (УКН);
-
выработка удельная в натуральном измерении (м3/чел-дн и м3/маш-см и т.д.).
В нашем случае для определения нормативной трудоемкости железобетонных работ были использованы ТЕРы, а именно:
-
устройство фундаментной плиты – ТЕР-06-01-001-16;
-
устройство стен и перегородок – ТЕР-06-01-031-09;
-
устройство плит перекрытия – ТЕР-06-01-041-03.
Согласно ТЕР-06-01-001-16 для устройства фундаментной плиты в объеме одной захватки необходимо 185 чел-смен и 24 маш-смен. Так как продолжительность выполнения фундаментной плиты на одной захватке принята 3 дня, то максимальное количество рабочих в день равно 185/3≈62 человека и 24/3=8 машинистов. Если работы ведутся в 3 смены, то единовременно на захватке будет находиться 62/3≈21 человек и 8/3≈3 машиниста. По аналогичной схеме определяется предельное количество рабочих и машинистов для остальных работ.
Далее по полученным данным о предельно возможном количестве рабочей силы строится календарный график. При этом, как отмечалось выше, работы в календарном графике должны описываться по определенной иерархии.
На втором этапе для приведения к линейному виду обратно пропорциональной зависимости продолжительности строительства от количества трудовых ресурсов необходимо ввести неопределенные ресурсные коэффициенты. Ресурсные коэффициенты определяются по следующей формуле:
![]() (1)
(1)
где a – неопределенный ресурсный коэффициент;
Rmax - максимальное число трудовых ресурсов;
R – оптимизируемое число ресурсов.
Из формулы (1) видно, что при уменьшении оптимизируемых ресурсов коэффициент a будет возрастать, а при Rmax=R, коэффициент будет равен нулю. Ограничением увеличения коэффициента a будет являться введение величины Rmin либо установление максимально возможных сроков строительства.
Введя неопределенный ресурсный коэффициент, продолжительность любой работы Т рассчитываем по формуле:
![]() (2)
(2)
где Tmin – это минимальная продолжительность выполнения работы, соответствующая максимуму ресурсов.
При составлении системы линейных уравнений необходимо учитывать растяжение фронтальных и ресурсных связей, а также ограничения на начала и окончания работ. Система линейных уравнений является линейным ограничением при поиске оптимального значения трудовых ресурсов.
Ресурсные связи связывают работу одной бригады на разных фронтах работ. Если бригада после завершения работы на одном фронте простаивает 3 дня и переходит на следующий фронт, то растяжение ресурсной связи будет равно трем.
Фронтальные связи связывают работу всех бригад на одном частном фронте. Если после завершения работы предшествующей бригады на данном фронте следующая бригада заступает спустя два дня, то растяжение фронтальной связи также будет равно двум дням.
Ограничения на начала и окончания работ накладывают соответственно начальные и конечные связи. Продемонстрируем составление линейных уравнений на фрагменте организационно-технологической схемы строительства МФК «Лахта Центр», представленном на рис. 4.
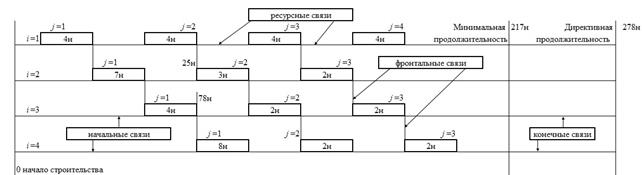
Рисунок 4. Фрагмент организационно-технологической схемы строительства МФК «Лахта Центр»
На фрагменте отражено выполнение 4 видов работ на 3 или 4 фронтах. Индекс i обозначает вид работ, j - номер частного фронта работ. Прямоугольники на рис. 4 показывают выполнение работы с ее продолжительностью в неделях при максимальном количестве ресурсов. Между работами показаны фронтальные и ресурсные связи, увязывающие работы на частных фронтах работ друг с другом. Также показаны начальные и конечные связи, накладывающие ограничения на начало и окончание работ соответственно. Например, работа № 3 на первом фронте не может окончиться позднее 78 недель, а вторая работа на втором фронте должна начаться не ранее 25 недель. Этими ограничениями мы учитываем промежуточные директивные сроки, устанавливаемые заказчиком.
Покажем особенности формирования системы линейных уравнений, состоящей из трех групп, в которые входят начальные, конечные и фронтальные уравнения.
Начальные уравнения включают в себя все связи и продолжительности работ одного вида, начиная с работы на текущем фронте и заканчивая работой на последнем фронте. Начальное уравнение для второго фронта второго вида работы будет определено следующим выражением:
278-25=5+a2·5+xb22+ xr22+xe23 , (3)
где 278-20 – определяется разностью между ограничением на окончание работы на последнем фронте и начало на втором фронте;
a2 - неизвестный ресурсный коэффициент для работ второго вида;
xr22 - растяжение 2-й ресурсной связи второго вида работ;
xb22 - растяжение начальной связи второго фронта;
xe23 - растяжение конечной связи третьего фронта.
Общее число начальных уравнений будет определяться общим числом фронтов всех работ.
Конечные уравнения включают в себя все связи и продолжительности работ одного вида, начиная с работы на первом фронте и заканчивая работой на текущем фронте. Конечное уравнение для первого фронта третьего вида работы будет определено следующим выражением:
78-0=4+a3·4+xb31+xe31 , (4)
Общее число конечных уравнений будет определяться общим числом фронтов всех работ минус число видов работ. Связано это с тем, что в каждом виде работ у начального и конечного уравнения будет одно общее. Благодаря сокращению количества конечных уравнений на величину видов работ дублирующие уравнения будут исключены. Например, дублирующими друг друга уравнениями для третьего вида работ будут начальное уравнение для 1-го фронта и конечное уравнение для 3-го фронта:
278-0=8+a3·8+xb31+ xr31+ xr32+xe33 , (5)
Фронтальные уравнения составляются для каждой фронтальной связи, они соединяют начальную часть верхней ветви уравнения и конечную часть нижней ветви уравнения. Фронтальное уравнение для второго фронта третьего вида работы будет определено следующим выражением.
278-0=10+a2·10+xb21+xr21+xf32+4+a3·4+xr32+xe33 , (6)
где xf32 - растяжение 2-й фронтальной связи работы третьего вида.
Общее число фронтальных уравнений будет определяться общим числом фронтальных связей. Всего для нашего фрагмента формируется 31 линейное уравнение.
Целевая функция для нашего фрагмента будет иметь следующий вид:
Z=16a1+12a2+8a3+12a4→max (7)
На третьем этапе производится оптимизационное уменьшение трудовых ресурсов путем решения полученной системы линейных уравнений. Решение производится классическим методом линейного программирования [10].
Результаты исследования
В результате проведения первого этапа получена минимальная продолжительность строительства, равная 1515 дням. Директивная продолжительность строительства, как отмечалось ранее, равна 1945 дням. Таким образом, оптимизационный потенциал равен 430 дням, что составляет 22%. Фрагмент календарного графика строительства МФК «Лахта Центр» в программном комплексе MP изображен на рисунке 5.
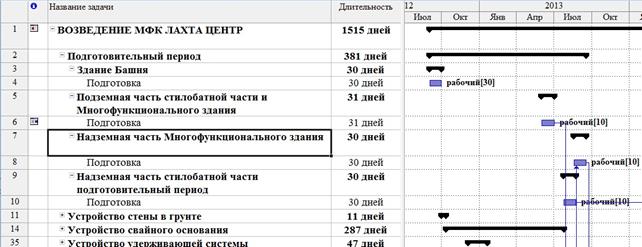
Рисунок 5. Фрагмент календарного графика строительства МФК «Лахта Центр» с максимальным использованием ресурсов
Выводы
В данной работе представлен укрупненный алгоритм решения ресурсной задачи для уникальных объектов с определением минимально необходимого количества трудовых ресурсов для соблюдения заданных сроков строительства. Применение укрупненного алгоритма проиллюстрировано на примере строительства многофункционального комплекса «Лахта Центр».
Рецензенты:
Колчеданцев Л.М., д.т.н., профессор кафедры организации строительства и управления недвижимостью Санкт-Петербургского архитектурно-строительного университета, г. Санкт-Петербург.
Бирюков А.Н., д.т.н., профессор, заведующий кафедрой технологии, организации и экономики строительства Военного института (инженерно-технического) Военной академии материально-технического обеспечения имени генерала армии А.В. Хрулёва в Санкт-Петербурге, г. Санкт-Петербург.



