В настоящее время, при рассмотрении организации производства на предприятии, можно обратить внимание на наличие противоречий между сотрудниками подразделений в конструкторско-технологической подготовке производства [1-4]. Согласованием интересов между сотрудниками занимается верхний уровень матричной структуры взаимодействия – руководители подразделений:
1) РКП – руководитель конструкторского подразделения;
2) РТП – руководитель технологического подразделения;
3) РПП – руководитель производственного подразделения.
Все эти руководители находятся в подчинении у руководителя организационной системы (РОС).
Главная задача руководителей подразделений заключается в предоставлении комфортных условий для работы, которые нужны сотруднику, включая и все необходимые орудия труда, не говоря уже о достойной оплате.
Но не все сотрудники одной квалификации, и, следовательно, не могут получать равную оплату и поощрения. Поэтому для определения количества оптимального финансирования вознаграждения, а также для проведения каких-либо действий для увеличения мотивации (побуждении) и стимулирования, заинтересованности сотрудников в увеличении объёма производства – нужно рассмотреть структуру, в которой будет отражаться взаимосвязь между исследуемыми объектами.
Для нахождения оптимального финансирования разработаем математическую модель методом управления ресурсами [5], где нам необходимо рассмотреть матричную структуру взаимодействия (рис. 1).
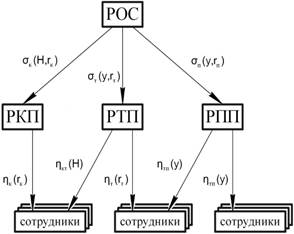
Рис. 1 – Матричная структура взаимодействия на ОАО «Волгабурмаш»
Целевые функции участников организационной системы, представленной на рис. 1, имеют вид:
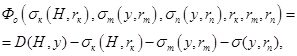 (1)
(1)
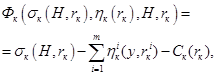 (2)
(2)
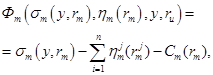 (3)
(3)
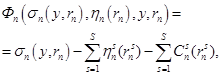 (4)
(4)
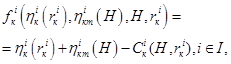 (5)
(5)
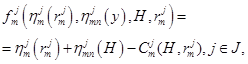 (6)
(6)
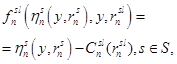 (7)
(7)
где ![]() – функция дохода организационной системы;
– функция дохода организационной системы;
![]() – бюджетные ресурсы, выделяемые конструкторскому (КП), технологическому (ТП) и производственному (ПП) подразделениям со стороны руководителя организационной системы (РОС);
– бюджетные ресурсы, выделяемые конструкторскому (КП), технологическому (ТП) и производственному (ПП) подразделениям со стороны руководителя организационной системы (РОС);
![]() – функции стимулирования КП, ТП и ПП;
– функции стимулирования КП, ТП и ПП;
![]() – функция стимулирования
– функция стимулирования ![]() –го конструктора со стороны ТП;
–го конструктора со стороны ТП;
![]() – функция стимулирования
– функция стимулирования ![]() –го технолога со стороны ПП;
–го технолога со стороны ПП;
![]() – функция стимулирования сотрудников
– функция стимулирования сотрудников ![]() –го ПП;
–го ПП;
![]() – функции затрат КП, ТП и ПП;
– функции затрат КП, ТП и ПП;
![]() – функции затрат
– функции затрат ![]() –го сотрудника
–го сотрудника ![]() –го подразделения;
–го подразделения;
![]() – качество (надёжность) изделия;
– качество (надёжность) изделия;
![]() – квалификация, соответственно, конструктора, технолога, сотрудника ПП.
– квалификация, соответственно, конструктора, технолога, сотрудника ПП.
В рассматриваемой модели матричной структуры задача взаимодействия, решаемая с точки зрения руководителя организационной системы, заключается в определении РОС бюджетных средств, побуждающих руководителей функциональных и производственных подразделений выбирать такие стратегии, которые максимизировали бы целевую функцию РОС (1). В свою очередь, руководители функциональных и производственных подразделений при заданных со стороны РОС объёмах бюджетных средств решают задачу определения систем стимулирования своих сотрудников, побуждающих их выбирать такие стратегии, которые максимизировали бы целевые функции РКП (2), РТП (3), РПП (4).
Основная трудность при решении задач взаимодействия заключается в том, что модели принятия решений по выбору параметров организационной системы в ограничениях содержат модели оптимизационных задач нижних уровней. В связи с этим в работе решают задачи согласованного взаимодействия нескольких двухуровневых иерархических систем – задач верхней и нижней иерархии.
Решением задачи взаимодействия является область параметров функции стимулирования, которая наиболее выгодна для РОС. В то же время эта область позволяет ставить и решать задачи выбора параметров, оптимальных с точки зрения функциональных подразделений и их сотрудников.
Рассчитаем математическую модель задачи согласованного взаимодействия в рассматриваемой организационной системе на примере машиностроительного предприятия.
Исходными данными для расчёта математической модели послужили данные, полученные в конструкторском и технологическом отделах машиностроительного предприятия.
Таблица 1 – Исходные данные для расчёта математической модели принятия решений на ОАО «Волгабурмаш»
|
Обозначение |
Числовое значение |
Условные доли |
|
|
120 шт. |
1,2 |
|
|
100 шт. |
1 |
|
|
20 шт. |
0,2 |
|
|
51000 руб. |
1 |
|
|
- |
0,5 |
|
|
- |
0,4 |
|
|
- |
0,1 |
Таблица 2 – Исходные данные для расчёта математической модели принятия решений РКП
|
Обозначение |
Числовое значение |
|
|
0,7 |
|
|
0,5 |
|
|
0,2 |
|
|
0,1 |
|
|
0,15 |
|
|
0,1 |
|
|
0,2 |
|
|
0,1 |
|
|
0,2 |
|
|
0,1 |
|
|
0,15 |
|
|
0,1 |
После подстановки исходных данных в модель задачи принятия решений руководителем конструкторского подразделения имеем:
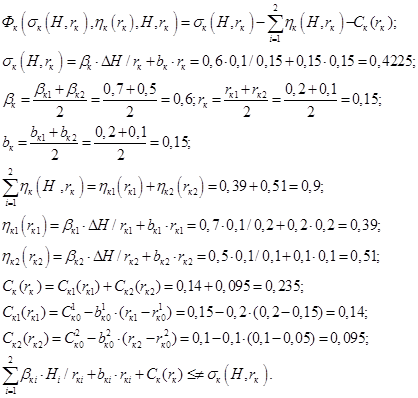 (8)
(8)
Таблица 3 – Исходные данные для расчёта математической модели принятия решений РТП
|
Обозначение |
Числовое значение |
|
|
0,8 |
|
|
0,6 |
|
|
0,2 |
|
|
0,1 |
|
|
0,05 |
|
|
0,1 |
|
|
0,2 |
|
|
0,1 |
|
|
0,1 |
|
|
0,05 |
|
|
0,2 |
|
|
0,1 |
После подстановки исходных данных в модель задачи принятия решений руководителем технологического подразделения имеем:

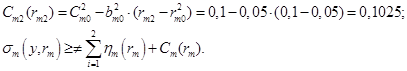 (9)
(9)
Таблица 4 – Исходные данные для расчёта математической модели принятия решений РПП
|
Обозначение |
Числовое значение |
|
|
0,7 |
|
|
0,5 |
|
|
0,2 |
|
|
0,1 |
|
|
0,2 |
|
|
0,1 |
|
|
0,2 |
|
|
0,1 |
|
|
0,1 |
|
|
0,1 |
|
|
0,4 |
|
|
0,2 |
|
|
0,7 |
|
|
0,5 |
После подстановки исходных данных в модель задачи принятия решений сотрудником производственного подразделения имеем:
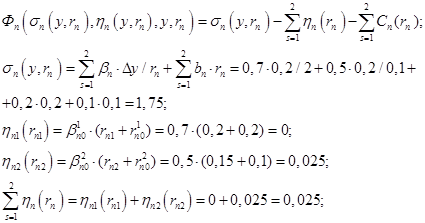
![]() (10)
(10)
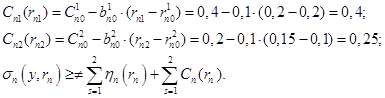
Выводы
При рассмотрении математической модели принятия решения РКП условие не выполнялось, следовательно, нам не нужен сотрудник высокой квалификации, так как с его задачами может справиться менее опытный специалист. Либо требовалось принудительно повышать бюджетные средства, которые выделялись сотрудникам от руководителей. Аналогичная ситуация проглядывается и с технологическим подразделением. Наличие данных моделей позволяет разработать систему автоматизации процессов конструкторско-технологической подготовки производства [6; 7].
При анализе математической модели принятия решения РПП выяснилось, что она требует доработки и добавления новых коэффициентов.
Разработанная модель согласованного взаимодействия участников конструкторско-технологической подготовки производства является удобным средством для принятия решений при повышении надёжности изделий, она позволяет устранить противоречия между конструкторским и технологическими подразделениями на уровне руководителей этих отделов. Это противоречие является актуальной проблемой для промышленных предприятий в области организации производства.
Рецензенты:
Хаймович И.Н., д.т.н., профессор кафедры информационных систем и компьютерных технологий НОУ ВПО «Международный институт рынка», г. Самара.
Макаров А.А., д.т.н., профессор, зав. кафедрой информационных систем и компьютерных технологий НОУ ВПО «Международный институт рынка», г. Самара.



