Введение
Надежность функционирования электроэнергетических систем (ЭЭС) в нормальных и особенно аварийных и послеаварийных режимах в значительной мере определяется правильностью работы средств релейной защиты и автоматики (РЗА), в том числе дистанционных защит (ДЗ), применяемых в качестве основных и резервных защит линий электропередачи (ЛЭП), резервных защит автотрансформаторов (АТ). Кроме этого, дистанционный принцип используется также при реализации защит от потери синхронизма синхронных генераторов (СГ), в устройствах автоматики ликвидации асинхронного режима (АЛАР) и ряде других средств РЗА. При этом согласно обобщенной статистике [3] неправильное функционирование РЗА, повлекшее аварийное изменение эксплуатационного состояния или режима работы указанных элементов ЭЭС, в 25 процентах случаев служит причиной тяжелых аварий. Поскольку поломки, дефекты, ошибки персонала, стихийные бедствия в данной статистике также учтены, основной причиной неправильного функционирования РЗА является несоответствие их настройки конкретным режимным условиям.
В силу того, что натурные эксперименты в ЭЭС, особенно аварийного характера, как правило, не допустимы, а также ввиду чрезмерной сложности полноценного физического моделирования ЭЭС основным инструментом для настройки и анализа функционирования РЗА являются средства математического моделирования ЭЭС и от их адекватности зависит успешность решения обозначенной проблемы. Основными критериями адекватного математического моделирования ЭЭС являются: 1) полнота и адекватность применяемых математических моделей основного и вспомогательного оборудования ЭЭС, включая РЗА, образующих совокупную модель ЭЭС; 2) возможность применяемых средств математического моделирования выполнять решение совокупной модели ЭЭС с необходимой гарантированной точностью.
С учетом достигнутого уровня физико-математического представления и описания процессов в ЭЭС, принципиальных ограничений выполнению первого из указанных критериев нет. Однако ввиду того, что совокупная математическая модель ЭЭС, даже с учетом частичного эквивалентирования, представляет жесткую, нелинейную систему дифференциальных уравнений чрезвычайно высокого порядка, точность ее решения согласно условиям применимости теории методов дискретизации для обыкновенных дифференциальных уравнений при помощи известных методов численного интегрирования не гарантирована. Учитывая вышесказанное, а также в результате анализа свойств и возможностей применяемых в настоящее время для настройки РЗА программных средств математического моделирования ЭЭС, таких как АРМ СРЗА, Мустанг, EUROSTAG, определено следующее: неизбежно используются значительные упрощения математических моделей основного и вспомогательного оборудования ЭЭС, включая РЗА, и ограничения условий их решения; математическое описание РЗА выполняется весьма упрощенно при помощи алгебраических уравнений и логических функций, погрешности, определяемые протеканием процессов в аппаратной части РЗА и в измерительных трансформаторах (ИТ) учитываются грубо посредством обобщённых коэффициентов.
Из вышесказанного следует, что несоответствующая конкретным режимным условиям настройка РЗА определяется двумя факторами:
1) недостаточная достоверность определения необходимых режимных величин;
2) грубый и обобщенный учет погрешностей, определяемых конкретной реализацией РЗА и ИТ.
С появлением более совершенных средств моделирования ЭЭС, таких как RealTimeDigitalSimulator (RTDS) [5], Всережимный моделирующий комплекс реального времени электроэнергетических систем (ВМК РВ ЭЭС) [4], стала возможной минимизация первого из указанных факторов. В частности, ВМК РВ ЭЭС, благодаря концептуальным особенностям программно-аппаратной реализации, предусматривающей методически точное неявное непрерывное интегрированиес гарантированной приемлемой инструментальной погрешностью систем дифференциальных уравненийматематической модели ЭЭС в специализированных гибридных процессорах [4], лишен указанных недостатков, свойственных сугубо программным средствам моделирования. Однако ввиду отсутствия в существующих средствах адекватного моделирования ЭЭС, включая ВМК РВ ЭЭС, достаточно адекватных математических моделей РЗА, в том числе ДЗ, а также методик и средств их реализации, необходимость снижения влияния второго фактора по-прежнему остается актуальной.
Целью исследований является определение эффективности анализа причин неправильного функционирования ДЗ, как одного из аспектов правильной настройки, при помощи разработанных всережимных математических моделей.
Материалы и методы
Синтез всережимных математических моделей ДЗ с учетом их конкретных реализаций и ИТ выполняется согласно разработанной методике всережимного моделирования. Под всережимным моделированием данный термин также используется в [4], в данном случае понимается возможность воспроизведения без декомпозиции всего значимого спектра протекающих в ИТ и аппаратной части ДЗ процессов во всевозможных режимах функционирования ЭЭС.
Методика всережимного моделирования ДЗ с учетом их конкретных реализаций и ИТ включает следующие этапы.
1. Разработка всережимных математических моделей
1.1 Анализ принципиальных схем и технических данных ИТ и ДЗ, в результате которого выделяются две группы функциональных элементов, учитываемых при моделировании: 1) элементы, с помощью которых выполняются логические операций с дискретными сигналами, аналого-цифровые и цифро-аналоговые преобразователи, прецизионной элементной базой которых гарантирована пренебрежимо малая величина вносимой ими погрешности, а также промежуточные и указательные реле, используемые в оперативных цепях ДЗ для размножения и усиления выходных сигналов; 2) элементы, выполняющие непрерывное преобразование аналоговых сигналов измеряемых режимных величин, точность преобразования аналоговых сигналов в которых определяется точностью преобразования их мгновенных значений: различные промежуточные преобразователи, входные фильтры, используемые в ДЗ схемы формирования и сравнения аналоговых сигналов.
1.2 Функциональные элементы, относящиеся к первой группе, описываются посредством логических функций и алгебраических уравнений, характеристики их аппаратной реализации принимаются идеальными. Функциональные элементы второй группы описываются передаточными функциями (ПФ), которые являются исходной математической основой, позволяющей производить их анализ во временной, частотной областях, и конвертируемых в дифференциальные уравнения.
Определение ПФ выполняется наиболее универсальным и эффективным в рамках данной задачи методом направленных графов [1] с использованием формулы Мэзона. Формирование направленных графов моделируемых функциональных элементов выполняется на основе их адекватных схем замещения. Для формирования адекватных схем замещения функциональных элементов ДЗ выполняется анализ их принципиальных схем. Пассивные функциональные элементы схем ДЗ, состоящие из диодов, резисторов, емкостей, катушек индуктивности, учитываются соответствующими активными сопротивлениями, емкостями, индуктивностями. Интегральные операционные усилители, используемые в схемах активных функциональных элементов, принимая во внимание их современные параметры, учитываются как идеальные.
1.3 Анализ полученных ПФ
Анализ полученных ПФ выполняется с целью определения элементов схем замещения, оказывающих существенное влияние на формируемые погрешности преобразуемых в них сигналов, а также элементов, влиянием которых можно пренебречь. В результате анализа определяется возможность обоснованного упрощения синтезируемых математических моделей. Анализ ПФ состоит из двух частей: 1) частотный анализ ПФ; 2) анализ ПФ в соответствии с теорией точности и чувствительности [6].
1.4 Полученные ПФ ИТ и функциональных элементов ДЗ конвертируются в дифференциальные уравнения. На основе алгебраических уравнений и логических функций, описывающих функциональные элементы первой группы, а также логических функций, систем алгебраических и дифференциальных уравнений, описывающих ИТ и функциональные элементы второй группы, синтезируется совокупная всережимная математическая модель ДЗ.
2. Программная реализация всережимных математических моделей ДЗ
2.1 Программная реализация всережимных математических моделей ДЗ в среде адекватных средств моделирования ЭЭС
Описание разработанных всережимных математических моделей ДЗ с учетом конкретных реализаций и ИТ выполняется при помощи языков программирования, основным требованием к которым является их пригодность для формализации синтезированных всережимных математических моделей, состоящих из логических функций, систем алгебраических и дифференциальных уравнений и их оперативного решения. Данному требованию в полной мере соответствуют языки высокого уровня, например, семейства Си.
Величина дифференциального порядка синтезированных математических моделей ДЗ и другие их характеристики полностью удовлетворяют условиям сравнительно простых методов их решения.
2.2 Программная реализация всережимных математических моделей ДЗ в среде MATLAB
Описание разработанных всережимных математических моделей ДЗ с учетом конкретных реализаций и ИТ выполняется при помощи элементов библиотеки Simulink. В программируемых на языке семейства Си блоках S-function выполняется программная формализация ИТ и функциональных элементов ДЗ. Данные блоки объединяются в функциональную блок-схему, аналогичную приведенной на рисунке 1. В качестве измеряемых режимных величин используются массивы мгновенных значений токов и напряжений: 1) полученных при помощи средств адекватного моделирования ЭЭС, таких как ВМК РВ ЭЭС, предусматривающих воспроизведение мгновенных значений токов и напряжений и их запись в виде массива чисел, например, в формате Сomtrade; 2) записанных посредством регистраторов аварийных событий (РАС) в формате Сomtrade для конкретных режимов функционирования защищаемого элемента ЭЭС (ЛЭП, АТ и др.); в данном случае, поскольку в формируемых при помощи РАС массивах уже учтены процессы в ИТ, их всережимные модели заменяются передаточными коэффициентами, обратными номинальным коэффициентам трансформации ИТ. В обоих случаях массивы токов и напряжений задаются и воспроизводятся в MATLAB при помощи блока Fromworkspace.
Согласно изложенной методике синтезирована всережимная математическая модель первой ступени распространённой ДЗ типа ШДЭ-2801 [2] (далее – модель ДЗ) для определения причин ее ложного срабатывания в одном из записанных при помощи РАС режимов работы защищаемой ВЛ 110кВ реальной энергосистемы. Синтезированная модель ДЗ представляет совокупность математических моделей измерительных трансформаторов тока (ИТТ), напряжения (ИТН) и трех комплектов реле сопротивления (РС) АВ, ВС, СА, включающих математические модели промежуточных трансформаторов тока (ПТН), напряжения (ПТН), формирователей сравниваемых величин (ФСВ), блоков памяти (БП), формирователей импульсов несовпадения (ФИН), реагирующих органов (для первой ступени используется реагирующий орган второго типа РО2 [2]), объединенных в MATLAB в соответствующую функциональную блок-схему

Рис. 1. Функциональная блок-схема всережимной модели первой ступени ДЗ ШДЭ-2801
В качестве примера приведена разработанная математическая модель ПТТ
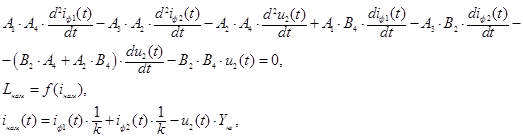
где ![]() – токи первой и второй первичной обмотки ПТТ, ток ветви намагничивания ПТТ, напряжение на вторичной обмотке ПТТ соответственно;
– токи первой и второй первичной обмотки ПТТ, ток ветви намагничивания ПТТ, напряжение на вторичной обмотке ПТТ соответственно;
А1,А2,В2,А3,А4, В4 – введенные для компактности записи дифференциального уравнения моделируемого ПТТ обозначения (аналогичные обозначения используются призаписи дифференциальных уравнений ИТТ, ИТН, ПТН и других функциональных элементов модели ДЗ):
 ;
; ![]() ;
; 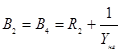 ;
;
![]() – параметры схемы замещения моделируемого ПТТ.
– параметры схемы замещения моделируемого ПТТ.
Математические модели ИТТ, ИТН, ПТН, БП, ФСВ, РО2 реализуются аналогичным образом, однако в данном случае поскольку в качестве режимных величин используются массивы РАС, формируемые с учетом процессов в ИТ, модели ИТТ и ИТН согласно методике учитываются передаточными коэффициентами, соответствующими их обратным номинальным коэффициентам трансформации. Математическая модель ФИН, выполняющего операции с дискретными сигналами [2], согласно методике описывается логической функцией.
Результаты исследований и обсуждение
Выполнено исследование функционирования разработанной модели первой ступени ДЗ ШДЭ-2801 ВЛ 110кВ в режиме качаний, воспроизведенном при помощи записанных РАС массивов токов и напряжений. Рассматриваемый режим качаний возник в реальной ЭЭС после ликвидации действием РЗА в сети 220кВ аварийного возмущения. Настройка моделируемой ДЗ выполнена в соответствии с картой уставок реальной ДЗ.
На рисунке 2 приведены осциллограммы токов и напряжений, полученные в программе MATLAB при помощи массивов РАС, а также соответствующие результаты сравнения сигналов срабатывания первой ступени модели и реальной ДЗ ШДЭ-2801.
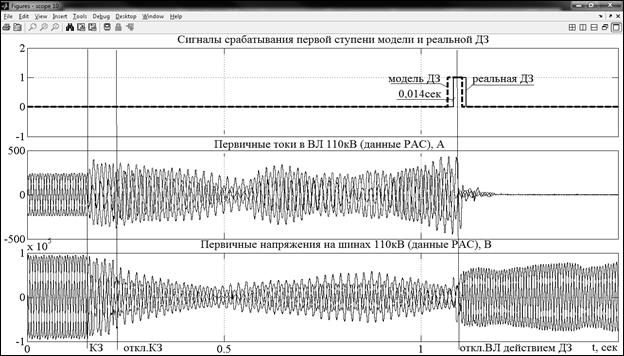
Рис. 2. Сравнение результатов функционирования модели и реальной ДЗ ШДЭ-2801
Приведенный на рисунке 2 сигнал срабатывания модели первой ступени ДЗ сформирован в результате функционирования комплекта РС АВ. Отличие по времени срабатывания модели и реальной ДЗ незначительно и составляет около 0,014 секунд.
На рисунке 3 приведены применяемые при анализе причин ложного срабатывания ДЗ результаты функционирования элементов сработавшего комплекта РС АВ.
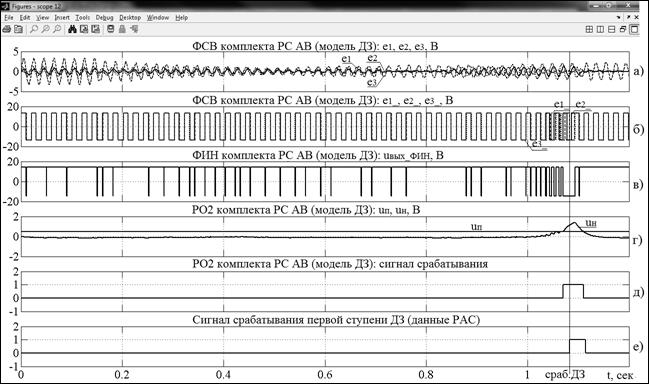
Рис. 3. Эксперементально полученные осцилограммы: а) формируемых на входе ФСВ сравниваемых величин е1, е2, е3; б) формируемых на выходе ФСВ импульсов е1_, е2_, е3_; в) формируемых на выходе ФИН импульсов; г) напряжение интегрирующего элемента РО2 uн сравнивается с пороговым напряжением uп; д) сигнал срабатывания моделируемой ДЗ; е) сигнал срабатывания реальной ДЗ
По принципу действия ДЗ не отстроена от срабатывания в режиме качаний без наличия соответствующего устройства блокировки. Согласно приведенным на рисунке 4 результатам исследований ложное срабатывание первой ступени ДЗ в режиме качаний произошло в результате выполнения условий срабатывания комплекта РС АВ: формируемое на выходе интегрирующего элемента напряжение uн превысило пороговое значение uп. Поскольку в модели ДЗ блокировка от качаний не учитывалась, аналогичное функционирование модели и реальной ДЗ в рассматриваемом режиме свидетельствует об отказе функционирования устройства блокировки от качаний в реальности. Причиной отказа могла послужить неисправность или неэффективность применяемой блокировки от качаний в сложившемся конкретном режиме.
Выводы
1. В результате выполненных исследований подтверждена адекватность разработанной всережимной математической модели ДЗ путем сравнения результатов ее функционирования с результатами функционирования реальной ДЗ ШДЭ-2801 ВЛ 110кВ в режиме качаний.
2. Полученными результатами исследований подтверждается эффективность применения разработанной всережимной математической модели ДЗ для анализа причин неправильного функционирования реальных ДЗ, как одного из аспектов их правильной настройки.
Рецензенты:
Кабышев А.В., д.ф.-м.н., профессор, профессор кафедры электроснабжения промышленных предприятий Энергетического института Национального исследовательского Томского политехнического университета, г. Томск.
Хрущев Ю.В., д.т.н., профессор, профессор кафедры электрических сетей и электротехники Энергетического института Национального исследовательского Томского политехнического университета, г. Томск.



