Проблемная экологическая ситуация наблюдается во многих городах России и зарубежных странах. Наиболее сильно техногенное геохимическое воздействие на природную среду и население проявляется в крупных промышленных центрах. Анализ ранее проведённых эколого-геохимических исследований твердого осадка снега и почв урбанизированных территорий в городах России и других стран показывает [5-10], что требуется анализ полученных результатов с использованием многомерного статистического анализа (МСА) для получения наиболее объективной информации [1-4]. Данные результаты позволят наиболее корректно подходить к принятию управленческих решений.
В связи с этим представляет интерес статистический анализ результатов эколого-геохимических измерений в твердом осадке снега на территории Кировского района г. Томска (СНЕГ_Т), где сосредоточены промышленные предприятия в селитебной зоне (табл. 1).
Таблица 1 - Содержание макро- и микроэлементов в твердом осадке снега на территории г. Томска (Na, Ca, Fe в %, остальные в мг/кг)
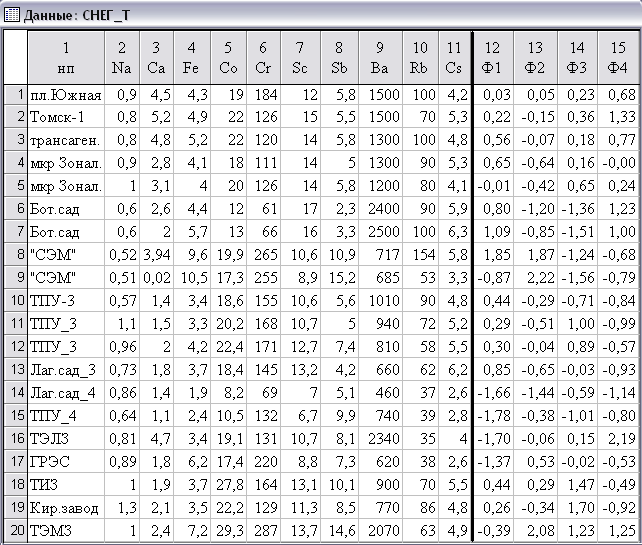
Наиболее значимыми по загрязнению территориями являются промышленные предприятия: СЭМ – «Сибэлектромотор», ТЭЛЗ – Томский электроламповый завод, ТИЗ – Томский инструментальный завод, Кир. завод – кирпичный завод, ТЭМЗ – Томский электро-механический завод и ГРЭС – городская районная электростанция. Кроме промышленных предприятий, на территории района расположены участки парковой зоны (Лаг. сад – Лагерный сад), территория университета (ТПУ – Томский политехнический университет), жилые районы (мкр. Зональный – микрорайон Зональный) и экспериментального хозяйства Сибирского ботанического сада (Бот. сад). Опробование снегового покрова на территории района проведено по сетке. Получено 20 проб снега, из которых после определенной подготовки выделен твердый осадок снега. Данная твердая фаза подвергалась инструментальному нейтронно-активационному анализу (ИНАА) в ядерно-геохимической лаборатории (аттестат аккредитации № РОСС RU.0001.511901) кафедры геоэкологии и геохимии ТПУ.
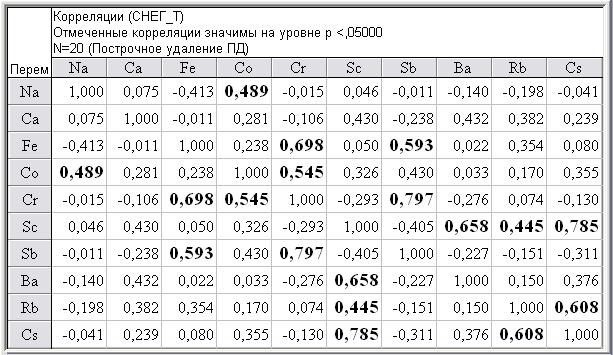
Корреляция между результатами содержаний двух химических элементов может приближенно характеризоваться коэффициентом парной корреляции Пирсона r (табл. 2).
Таблица 2 - Корреляционная матрица химических элементов СНЕГ_Т
Результаты кластер-анализа СНЕГ_Т изображены в виде дендрограммы (рис. 1), в которой по оси абсцисс располагаются символические обозначения химических элементов, а по оси ординат значение 1 – r , соответствующее каждому иерархическому уровню группирования. Как следует из рис. 1, значимыми (на уровне значимости p < 0,10) геохимическими ассоциациями элементов в снеговом покрове являются 4 составных кластера, которые отражают специфику производства промышленных предприятий:
{Sc–Cs–Rb} – ассоциация редких элементов,
{Cr– Sb– Fe} – ассоциация тяжелых металлов,
{Ba– Ca} – ассоциация тяжелого металла Ba с макроэлементом Ca,
{Co– Na} – ассоциация тяжелого металла Co с макроэлементом Na.
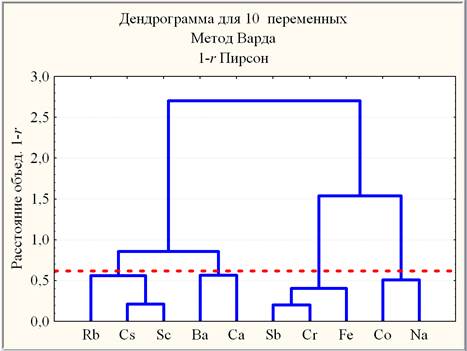
Рис. 1. Дендрограмма корреляционной матрицы геохимического спектра микроэлементов СНЕГ_Т (пунктирная прямая критического уровня: 1-r0,10 = 0,62; n = 20)
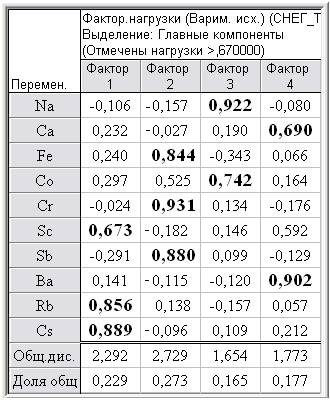
Наличие корреляционной зависимости элементов допускает использование факторного анализа, основанного на оценках корреляций (факторных нагрузок) между исходными элементами и факторами, образованными группами корреляционно связанных исходных элементов. На основании факторного анализа проведено сокращение числа рассматриваемых элементов и определена структура взаимосвязей между элементами, т.е. классификация элементов. Самую важную информацию, на которой базируется интерпретация факторов, содержат факторные нагрузки, которые могут интерпретироваться как корреляции между факторами и переменными (табл. 3). Согласно табл. 3, высокие факторные нагрузки элементов распределились по факторам следующим образом.
Фактор Ф1 – фактор редких элементов {Cs–Rb– Sc}, связанных с Ф1 положительной корреляционной связью.
Фактор Ф2 – фактор тяжелых металлов {Cr– Sb– Fe}, связанных с Ф2 положительной корреляционной связью.
Фактор Ф3 – фактор смешанный {Na– Co} макроэлемента Na с тяжелым металлом Co, связанных с Ф3 положительной корреляционной связью.
Фактор Ф4 – фактор смешанный {Ba– Ca} тяжелого металла Ba с макроэлементом Ca, связанных с Ф4 положительной корреляционной связью.
Таблица 3 - Вращаемые факторные нагрузки в выбранной 4-факторной модели ЭГХИСТ
Для проведения дальнейшего статистического анализа ЭГХИСТ в рамках построенной 4-факторной модели вычислены значения наблюдений в новой системе факторных координат {Ф1, Ф2, Ф3, Ф4} (табл. 1).
В построенном 4-мерном факторном пространстве {Ф1, Ф2, Ф3, Ф4} проведена кластеризация наблюдений (рис. 2).
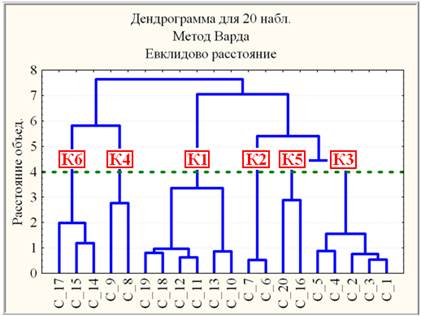
Рис. 2. Дендрограмма наблюдений в пространстве {Ф1, Ф2, Ф3, Ф4}
При этом в качестве меры близости выбрано расстояние Евклида, а в качестве правила объединения двух кластеров использован дисперсионный анализ, по сути метод Варда. Методом древовидной кластеризации построено иерархическое дерево (рис. 2). В зависимости от выбора расстояния объединения можно получить соответствующее число кластеров. Так, например, расстоянию объединения, равному 4 (пунктирная горизонтальная прямая), соответствует 6 кластеров. Увеличивая расстояния объединения, можно отслеживать динамику объединения кластеров по мере уменьшения степени их однородности. В данном случае выделенные кластеры соответствуют как территориальному признаку, так и специфике производств промышленных предприятий. Из выделенных кластеров наиболее четко соответствуют территориальному признаку расположения: К1 – учебное заведение (ТПУ) и парковая зона (Лаг. сад), К2 – экспериментальное хозяйство Сибирского ботанического сада и К3 – жилая застройка. Тогда как из кластеров, соответствующих специфике производства промышленных предприятий, следует выделить К4, характеризующий территорию промышленного предприятия «Сибэлектромотор», а К5 – Томский электромеханический и Томский электроламповый заводы. Для кластера К6 не наблюдается выше указанной особенности.
Наряду с методом древовидной кластеризации применяется также метод K-средних, проводящий классификацию объектов (наблюдений) по заданному количеству кластеров. Алгоритм метода K-средних, перемещая объекты в разные кластеры с целью минимизации изменчивости внутри кластеров и максимизации изменчивости между кластерами, оценивает качество кластеризации наблюдений по каждому фактору посредством параметрического дисперсионного анализа (табл. 4).
Таблица 4 - Результаты дисперсионного анализа кластеризации наблюдений по факторам ЭГХИСТ
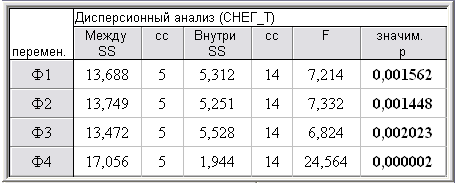
Признаком хорошей классификации является малость изменчивости внутри кластера в сравнении с изменчивостью вне кластера, что осуществляется путём стандартного межгруппового дисперсионного анализа для каждого фактора. Результаты дисперсионного анализа, приведенные в таблице 4, свидетельствуют о высоком качестве (на уровне значимости р < 0,005) разбиения 20 наблюдений на 6 кластеров по каждому фактору. Графики факторных средних для каждого кластера приведены на рисунке 3.
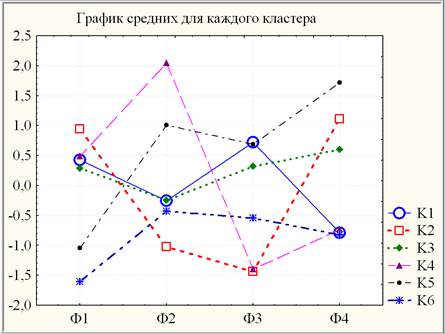
Рис. 3. Линейные графики факторных (стандартизированных) средних для каждого кластера
Полученные результаты кластеризации наблюдений методом K-средних в полной мере соответствуют иерархическому дереву (рис. 2), построенному методом древовидной кластеризации. В данном случае в качестве меры близости выбрано евклидово расстояние, а в качестве правила объединения двух кластеров использован метод Варда.
По критерию Фишера НЗР можно оформить результаты множественных сравнений кластерных средних для каждого фактора:
Ф1: {К2, К4, К1, К3}, {К5, К6} так, что К3 (mK3≈0,29) отличается от К5 (mK5≈-1,046) статистически значимо (на уровне значимости р ≈ 0,022).
Ф2: {К4, К5}, {К3, К1, К6, К2} так, что К5 (mK5≈1,01) отличается от К3 (mK3≈-0,25) статистически значимо (на уровне значимости р ≈ 0,028).
Ф3: {К1, К5, К3}, {К3, К6}, { К6, К4, К2} так, что К5 (mK5 ≈ 0,67) отличается от К6 (mK6 ≈ -0,54) слабо значимо (на уровне значимости р ≈ 0,051), а К3 (mK3 ≈ 0,32) отличается от К4 (mK4 ≈ -1,40) статистически значимо (на уровне значимости р ≈ 0,006).
Ф4: {К5, К2}, {К2, К3}, {К4, К1, К6} так, что К3 (mK3 » 0,60) отличается сильно значимо (на уровне значимости 0,0005< р < 0,005) как от К5 (mK5≈1,72), так и от К4 (mK5≈-0,74).
Результаты кластерного анализа наблюдений по совокупности факторов с учетом результатов сравнений кластерных средних для каждого фактора позволяют провести классификацию наблюдений в порядковой шкале стандартизированных измерений, полагая в качестве уровня «Средний+» – стандартизированный интервал (0,0; +1,25) наблюдений, «Выше среднего» – (> +1,25) наблюдений, «Средний–» – стандартизированный интервал (-1,25; -0,0) наблюдений, «Ниже среднего» – (< -1,5).
Таблица 5 - Классификация наблюдений по совокупности факторов в порядковой шкале стандартизированных измерений
|
Клас- тер |
Уровень кластера на фоне среднего по фактору |
Состав кластера |
|||
|
Ф1 {Cs–Rb– Sc} |
Ф2 {Cr– Sb– Fe} |
Ф3 {Na– Co} |
Ф4 {Ba– Ca} |
|
|
|
К1 |
Средний+ |
Средний– |
Средний+ |
Средний– |
С_10–13,18,19 |
|
К2 |
Средний+ |
Средний– |
Ниже среднего |
Средний+ |
С_6, 7 |
|
К3 |
Средний+ |
Средний– |
Средний+ |
Средний+ |
С_1–5 |
|
К4 |
Средний+ |
Выше среднего |
Ниже среднего |
Средний– |
С_8, 9 |
|
К5 |
Средний– |
Средний+ |
Средний+ |
Выше среднего |
С_16, 20 |
|
К6 |
Ниже среднего |
Средний– |
Средний– |
Средний– |
С_14, 15, 17 |
Для достоверности полученных результатов дисперсионного анализа необходимо проверить предположения о нормальном распределении сравниваемых кластеров и об однородности дисперсий в них. Но в данном случае достаточно замечания о малочисленности состава кластеров, чтобы обратиться к непараметрическому однофакторному дисперсионному анализу на основе критерия Краскела-Уоллиса, по которому 6 кластеров различаются слабо значимо в случае Ф2 (на уровне значимости р » 0,08) и статистически значимо (на уровне значимости 0,005 < р < 0,05) в случае Ф1, Ф3 и Ф4. По критерию Краскела-Уоллиса результаты множественных сравнений кластерных средних для каждого фактора можно оформить в следующем виде:
Ф1: {К2, К4, К1, К3, К5}, { К4, К1, К3, К5, К6} так, что К2 отличается от К6 слабо значимо (на уровне значимости р ≈ 0,07).
Ф2: {К4, К5, К3, К1, К6}, { К5, К3, К1, К6, К2} так, что К4 отличается от К2 слабо значимо (на уровне значимости р ≈ 0,08).
Ф3: {К1, К5, К3, К6}, { К3, К6, К4, К2} так, что К1 отличается от К2 статистически значимо (на уровне значимости р ≈ 0,046).
Ф4: {К5, К2, К3}, { К2, К3, К4, К1, К6} так, что К5 отличается от К6 слабо значимо (на уровне значимости р ≈ 0,08).
Таким образом, непараметрический дисперсионный анализ подтверждает (в смягченной форме) результаты параметрического дисперсионного анализа (табл. 4) о значимой кластеризации наблюдений ЭГХИСТ. В силу расхождения результатов непараметрического и параметрического однофакторного дисперсионного анализа в связи с малочисленностью состава кластеров более корректными признаются результаты непараметрического дисперсионного анализа.
Результаты исследований, приведенных в статье, согласуются с известными результатами исследований проведенного эколого-геохимического зонирования всей территории г. Томска по факту загрязнения компонентов природной среды и позволяют с учетом доказательной базы, основанной на результатах статистического анализа, провести управленческие решения. В данном случае рекомендуется в первую очередь вывод за пределы территории города промышленных предприятий – «Сибэлектромотор» и Томского инструментального завода.
Выводы
1. Как следует из таблицы 2, в твердом осадке снега г. Томска наиболее значимые корреляционные связи в ассоциациях имеют две пары {Cs– Sc}и {Cr– Sb}. Для первой пары значимая корреляция трудно объяснима, тогда как для второй пары характерна специфика производства промышленного предприятия «Сибэлектромотор».
2. Построена 4-факторная модель ЭГХИСТ: Ф1 – фактор редких микроэлементов {Cs–Rb– Sc}, Ф2 – фактор тяжелых металлов {Cr– Sb– Fe}, Ф3 – фактор смешанный {Na– Co} макроэлемента Na с тяжелым металлом Co и Ф4 – фактор смешанный {Ba– Ca} тяжелого металла Ba с макроэлементом Ca, объясняющая » 84,5% от общей дисперсии.
3. На основе 4-мерного факторного пространства {Ф1, Ф2, Ф3, Ф4} построена 6-кластерная модель наблюдений, высокое качество которой по каждому фактору оценено F–критерием в рамках параметрического дисперсионного анализа (на уровне сильной значимости р < 0,005) и подтверждено непараметрическим критерием Краскела-Уоллиса в смягченной форме (на уровне слабой значимости 0,05 < р < 0,10). В данном случае наблюдается четко выраженная кластеризация от жилых районов менее загрязненных к территориям промышленных предприятий, где преимущественно сосредоточены повышенные концентрации тяжелых металлов.
4. Для каждого фактора на основании критериев множественных сравнений проведена классификация кластеров наблюдений в порядковой шкале стандартизированных факторных измерений. Например, по фактору тяжелых металлов Ф2 самый низкий уровень имеет кластер К2 (территория экспериментального Сибирского ботанического сада), затем уровень чуть выше, однородный с К2, имеют кластеры К6 (район Лагерного сада), К1 (район учебных корпусов университета) и К3 (жилой район), далее повышенный уровень, значимо отличающийся от К2, имеет К5 (заводы ТЭЛЗ и ТЭМЗ) и самый высокий уровень – у К4 (завод «Сибэлектромотор»).
Работа выполнена при поддержке Российского научного фонда.
Рецензенты:
Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.
Савичев О.Г., д.г.н., профессор кафедры гидрогеологии, инженерной геологии и гидрогеоэкологии, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.



