После термообработки подшипниковые кольца приобретают неплоскостность (изогнутость) торцовых поверхностей под действием остаточных температурных напряжений. Касание кольца с поверхностью стола и торцом круга при шлифовании будет происходить не по всей поверхности торца кольца. Упругие осевые перемещения, неизбежно возникающие при шлифовании торцов колец, будут влиять на режимы технологического процесса шлифования и их необходимо учитывать при совершенствовании технологических процессов [1].
Наибольшие осевые перемещения будут иметь кольца при двухточечном касании с поверхностью стола и торцом круга (рис. 1, а). Кольцо нагружено сосредоточенными силами Р (от действия шлифовального круга) и равномернораспределенной нагрузкой q (от действия магнитного поля стола), перпендикулярными плоскости кольца.
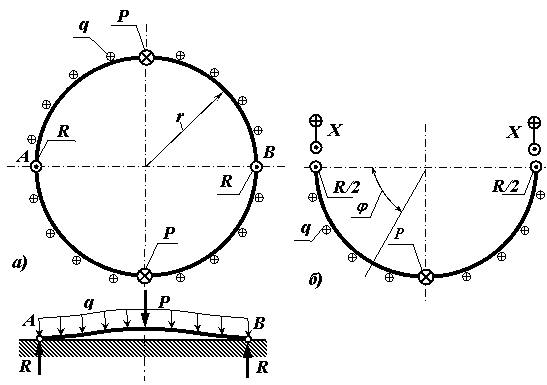
Рис. 1. Расчетная схема
В общем случае главные центральные оси поперечного сечения кольца, z и у, могут быть наклонены по отношению к плоскости кольца. Для облегчения дальнейших вычислений целесообразно ввести вспомогательные коэффициенты: hy = Iуc/ Izc; hzy = Iуczc/ Izc; hк = EIуIz/(GIzcIк); где Iуc, Izc, Iу, Iz, Iуczc- осевые и центробежный моменты инерции; Iк - момент инерции сечения при кручении; E, G – модули упругости и сдвига, соответствено. Центральная ось zc лежит в плоскости кольца, а ось уc - перпендикулярна этой плоскости.
Для раскрытия статической неопределимости используем свойства симметрии. При нагрузке перпендикулярной плоскости кольца, если провести разрез по оси, проходящей через точки А и В, неизвестным останется только изгибающий момент X1 (рис. 1, б) [2].
В этом случае момент X1 найдем из условия равновесия половины кольца. Составляя уравнение моментов относительно оси А-В, получим:
![]()
Реакции R в точках контакта определяются из суммы проекций всех сил на ось перпендикулярную плоскости кольца. В результате получим: R = (pqr + P)/2.
Для вычисления методом Мора перемещения в точке приложения силы достаточно проинтегрировать выражения моментов только для четверти круга (рис. 1, б), а результат умножить на 4 [2]:
![]()
Изгибающие и крутящие моменты в текущем сечении от действия внешней нагрузки Mzc, Mк и единичной силы M Izc, M Iк будут равны:
![]()
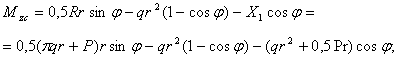
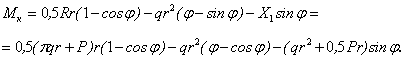
После интегрирования выражение для перемещения примет вид:
![]()
Определим осевое перемещение при шлифовании наружного кольца конического однорядного роликоподшипника с размерами D = 375 мм, С = 18 мм; D1 = 357,47 мм; D2= 367,1 мм; β = 15° (рис. 2).
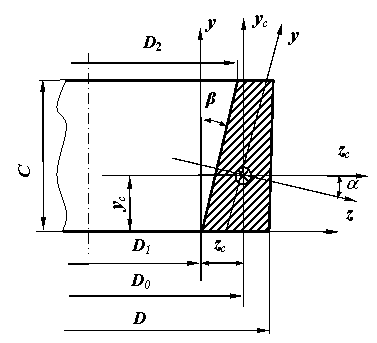
Рис. 2. Поперечное сечение кольца
Координаты центра тяжести поперечного сечения кольца yc, zc, диаметр центральной окружности D0 и моменты инерции будут равны: yc= 7,86 мм; zc= 5,44 мм; D0 = D1 + 2zc= 357,47 + 2×5,44 = 368,35 мм; Izc = 2755 мм4; Iyc = 495,2 мм4; Izcyc = 394,4 мм4; Iz = 2840 мм4; Iy = 410 мм4; a = -19,20.
Момент инерции при кручении вычисляем по формуле Гриффитса-Прескота [2]:
![]()
Вспомогательные коэффициенты будут равны: hy = 0,18; hzy = 0,143; hк = 0,63. Максимальное перемещение будет равно:

Формулы рекомендуется использовать для определения оптимальных режимов технологического процесса шлифования.
СПИСОК ЛИТЕРАТУРЫ
1. Коротков Б. И., Коротков С. Б., Тышкевич В. Н., Орлов С. В. Исследование процессов шлифования внутренних и наружных конусов деталей класса колец: Монография/ Под ред. Б. И. Короткова/ ВолгГТУ. – Волгоград, 2007. – 133 с.
2. Прочность, устойчивость, колебания. Справочник в трех томах. Т. 1 / Под ред. И.А. Биргера, Я.Г. Пановко – М.: Машиностроение, 1988. – 832 с.



