Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Линнеевский вид – сложная система – это есть целое, состоящее из связанных друг с другом частей. Изменчивость в форме может быть сведена к геометрическим схемам. В работах [3,4] мы подробно говорили о гармонической связи целого и части по принципу золотого отношения, по ряду Фибоначчи. Построенные Н.И. Вавиловым таблицы, из которых выведен закон гомологических рядов, дают возможность сравнивать их с таблицей Менделеева. В работе [5] указано, что таблица Менделеева соткана из золотых отношений. По-видимому, и в законе гомологических рядов, в котором принцип подобия и ритмичность являются основой, можно найти резонансы, связанные с золотыми числами [6].

Как известно [1,3], экспансия (расширение) развития (эволюции) вида берет начало от точки сингулярности. Учение Н.И. Вавилова о географических центрах происхождения культурных растений указывает на экспансию последних, распространение по всему земному шару. Для эволюции видов характерно единство прерывности и непрерывности, что говорит о взаимосвязи целого и его частей. «Закон гомологических рядов в наследственной изменчивости проявляется как определенная общая тенденция, присущая организмам (животным) и обусловленная общностью свойств организмов…».

Посредством скрещивания можно комбинировать одни признаки с другими и получать константные формы с новыми признаками, равно как в таблице Менделеева заполнять пустые клетки. В образовании новых видов, в частности, злаковых – важнейших в хозяйственном отношении семейств – на наш взгляд, одним из важных условий является бифуркационный переход из одного фазового состояния в другое. Назовем малыми бифуркационными переходами те, которые меняют второстепенные признаки растений и большими – основные, видовые признаки. Под изменчивостью понимается способность организмов приобретать новые признаки и свойства благодаря изменению молекул ДНК, в результате чего и возникает разнообразие. Спирали ДНК подчиняются принципам строения форм по золотой пропорции [3-5]. Динамическое золотое отношение является одним из универсальных законов природы, обеспечивающих подобие и целесообразность структур. Ряд Фибоначчи, ряд размножения имеет вид [6]:

,                                                  (1)

где  – золотое число, полученное при делении отрезка в крайнем отношении. Если мы берем ряд (1), например, как последовательность

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …                             (2)

обладающую аддитивным и мультипликативным свойствами, то при  имеем , при  –  и т.д.

Ритмичность в поведении целых организмов и их частей, включая растения, в частности, злаковые культуры; животных и человека, сказывается не только в формообразовании (например, по золотому числу), размножении (рост количества зерен в подсолнухе, колосе, шишке по ряду Фибоначчи), а также в вариациях, соответствующих пространственным и временным колебаниям геомагнитного поля Земли (ГМП). Любые организмы могут различить интенсивность магнитного поля и чувствовать направление, по которому магнитные силовые линии проходят через их тело.

В настоящей работе предлагается, разработанная нами [7-10], модель силовых линий магнитного поля Земли, рассчитанных для различных широтных регионов. Магнитное поле Земли считается потенциальным. Составляющие магнитного поля Земли могут быть выражены через градиенты потенциала.

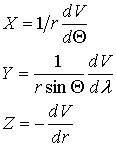,                                                    (3)

где Х – северная составляющая магнитного поля, направленная по меридиану, Y – восточная по параллели, Z – вертикальная по радиус-вектору, r – к центру Земли.  – географическая коширота точки наблюдения, j и l – географические широта и восточная долгота её.

Модуль полной напряженности поля определится как .

Магнитный потенциал, создаваемый на расстоянии h=r-R от шаровой поверхности радиуса R, вызванный источником внутри шара, представится рядом:

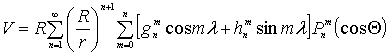 ,                  (4)

где ,  – коэффициенты разложения,  – нормированные присоединенные полиномы Лежандра [7-10], имеющие вид:

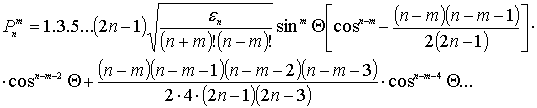, (5)

где  для ,  для .

Для решения поставленной задачи мы ограничились шестью членами разложения в выражении (4). Уравнение (3) преобразуется к виду:

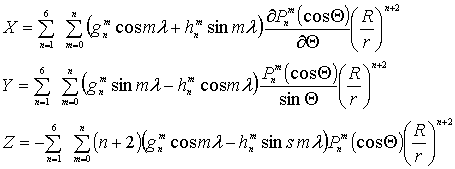.   (6)

Первый член разложения представляет потенциал, созданный однородно намагниченным шаром, второй – созданный двумя диполями - квадруполь и т.д.

Гауссовы коэффициенты определялись по наблюдаемым элементам X, Y, Z магнитного поля Земли в некоторых точках земной поверхности, распределенных более или менее равномерно. Нами использовались коэффициенты сферического гармонического анализа, из которых были выделены коэффициенты внутренней части поля  и  [7-10].

Для определения координат точек , расположенных по дуге силовой линии магнитного поля Земли через равные промежутки  длины дуги, решалась система дифференциальных уравнений:

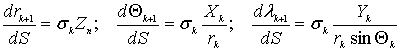,                (7)

где  – искомые координаты текущей точки, выбранной на силовой линии; 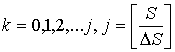, S – длина всей силовой линии;  – координаты начальной точки, , где R – радиус Земли. 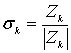 – если силовая линия строится в сторону от Земли,  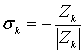– если силовая линия строится к Земле,  – образуют единичный вектор касательной к силовой линии, т.е. 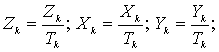. Система решалась численно.

В результате получены силовые линии магнитного поля и их параметры. На графике (рис. 1) представлена силовая линия, опирающаяся на широту Иркутска. Длина силовой линии между Иркутском и сопряженной точкой оказалась равной 23579 км. Данные по индукции магнитного поля (В) и магнитному наклонению (J) сведены в табл. 1.

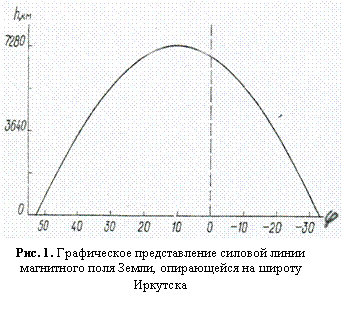
Таблица 1

Параметры силовой линии магнитного поля Земли, опирающейся на широту Иркутска

Высота над Землей	Северное полушарие, высота	Магнитное наклонение	В 10-4 т	Южное полушарие, широта	Магнитное наклонение	В 10-4 т
26	52°44’	70°30’	0,580	33°50’	-69°00’	0,552
455	51°29’	69°30’	0,472	32°19’	-67°20’	0,444
910	49°58’	67°10’	0,379	30°07’	-65°30’	0,362
1820	46°32’	63°50’	0,250	27°04’	-61°30’	0,243
2730	43°29’	58°00’	0,172	23°21’	-57°10’	0,168
3640	39°29’	53°00’	0,122	19°21’	-52°10’	0,120
4550	35°23’	47°00’	0,088	15°21’	-46°30’	0,087
5460	30°40’	139°30’	0,066	10°06’	-39°10’	0,064
6370	24°42’	29°00’	0,047	4°34’	-28°40’	0,047
7266	10°12’	0°	0,035

 

В настоящее время, благодаря развитию синергетики, стало возможным с единых позиций рассмотреть многие явления живой и неживой природы. Одним из таких явлений можно считать гомеостаз системы.

Находясь в состоянии гомеостаза, т.е. в состоянии аттрактивности, система достаточно легко адаптируется к внешним условиям, создавая отрицательные обратные связи с окружающей внешней средой. Биологический аттрактор приводит живой организм в состояние стационарного равновесия, устойчивости. Для практических целей прогноз и исследование всех видов равновесия, особенно связанных с продолжительностью жизни системы, является достаточно актуальной задачей.

Известно, что все природные аттракторы состоят из трех компонентов: притягивающего элемента, объекта притяжения, продукта действия системы. В рассматриваемом случае, притягивающими свойствами обладает магнитное поле Земли, благодаря индукции (B). Объектами притяжения служат, например, вода в живых организмах и электромагнитное поле клетки, обусловленное ее биоэлектрогенезом [11].

Уместно отметить, что Н.И. Вавилов рассматривал вопросы, связанные с географической изменчивостью зерновых культур. Так, продвижение пшеницы на 37° по долготе с запада на восток, а именно от 33° до 70° долготы, при той же широте, увеличивало содержание белка в сортах пшеницы с 11,6 до 21,1%. Картофель одного и того же сорта при перемещении на юг на каждый градус широты теряет 5% крахмала. Возможно, подобные изменения связанны не только с географической широтой, но и с магнитными координатами Земли ей соответствующими.

Магнитное поле оказывает заметное воздействие на живое. Так, семена хвойных пород прорастают на 4-5 дней быстрее, если они посажены корешками зародышей на юг, при такой же ориентации у кукурузы увеличивается листовая и зерновая масса растений. У огурцов наоборот – направление на север зародышевого корешка обеспечивает больший урожай.

Обнаружено, что многие животные ориентируются по магнитному полю: рыбы, птицы, пчелы. У человека известным фактором является наличие корреляции между частотой сердечного ритма и изменением магнитного наклонения, происходит изменение  ритма головного мозга, изменяются артериальное давление, электрическая активность кожных покровов, мышечная сила. В аномальных районах резко повышается заболеваемость гипертонией, ревматизмом, нервно-психическими болезнями.

Солнечная и магнитная активность оказывают также большое влияние на создание устойчивой сырьевой базы [9].

Таким образом, сложные системы биосферы, в частности растения, животные, человек, подвергаются воздействию солнечных, магнитных полей и описываются современными методами синергетики, включая автоволновые процессы, имеют ритмичность подобно гомологическим рядам Н.И. Вавилова.

Разработанная нами модель геомагнитного поля (ГМП) с одной стороны может быть использована при обработке эмпирического материала и нахождении корреляционной зависимости от параметров ГМП, а также может в модельном виде быть введена в информационно-синергетические модели скорости роста численности биологических объектов, подобно модели биогенного круговорота веществ и наших моделей [6,12].

 

СПИСОК ЛИТЕРАТУРЫ

1.   Кутимская М.А., Волянюк Е.Н. О возможностях применения принципов синергетики сложных систем в сельском хозяйстве. / Материалы региональной научно-практиче-ской конференции «Актуальные проблемы АПК». – Иркутск: ИрГСХА, 2001. – С. 54-55.

2.   Вавилов Н.И. Закон гомологических рядов и наследственной изменчивости. – Ленинград: Наука, 1987. – 260 с.

3.   Кутимская М.А. Физические основы пропорциональности биологических систем. – Иркутск: ИрГСХА, 1996. – 19 с.

4.   Кутимская М.А. Волянюк Е.Н. Учебный процесс как поиск новых познавательных ориентиров высокого уровня сложности. / Материалы VII межрегиональной НПК «Проблемы содержания и методики преподавания предметов физико-математического цикла». – Иркутск: ИрГСХА, 2000. – С. 6-9.

5.   Шевелев И.М., Марутаев М.А., Шмелев И.П. Золотое сечение: три взгляда на природу гармонии. – М.: Стройиздат, 1990. – 343 с.

6.   Кутимская М.А., Волянюк Е.Н. Бионоосфера: учеб. пособие. – Иркутск: Иркут. ун-т., 2005. – 212 с.

7.   Кутимская М.А., Кузьмин В.Н. Расчет силовых линий магнитного поля Земли. / Геомагнетизм и аэрономия. – М.: Наука, 1969. – 
Т. 9. - № 3. – С. 575.

8.   Кутимская М.А., Кузьмин В.Н. Модель замкнутой магнитосферы. / Исследования по геомагнетизму, аэрономии и физике Солнца. – М.: Наука, 1971. - № 13. – 300 с.

9.   Кутимская М.А. Влияние солнечной активности и магнитных полей на создание устойчивой сырьевой базы./ Товароведение и экспертиза товаров: проблема качества и потребительские свойства товаров. Вып. 2. – Иркутск: ГОУ ВПО ИГУ, 2006. – С. 47-53.

10.    Kutimskaya M.A., Jozefaciuk G, Wrraszcz E, Buzunova M.U. Effect of magnetic fields and plants vital activity. /Physics in agricultural research. International Scientific Conference. Papers and short communication. – June 12-13, 2008, Lublin, Poland. – P. 13-18.

11.    Кутимская М.А. Жизнь с точки зрения физики./ Вестник Иркутского регионального отделения высшей школы. – Иркутск: ИРО ВШ, 2003. – С. 122-128.

12.    Кутимская М.А., Волянюк Е.Н., Убрятова Л.В. Информационно-синергетиче-ское моделирование объектов биосферно-ноосферного комплекса./ Природные и интеллектуальные ресурсы Сибири (Сибресурс-8-2002): Доклады 8 МНПК. – Томск: Томск. ун-т, 2002. – С. 137-140.