Введение
Главная особенность входа орбитальных космических летательных аппаратов (КЛА) в плотные слои атмо сферы заключается в том, что скорость входа с орбиты не превышает пер вую космическую. В процессе полета аппарата в атмосфере осуществляется переход кинетической энергии в тепловую. Это определяет вид теплового воздействия, главным образом конвективный нагрев, интенсивность которого зависит от кинетической энергии аппарата на орбите. Последняя, как известно /1/, определяется его массой и орбитальной скоростью.
Суммарное количество теплоты, которое может выделиться у поверхности аппара та во время аэродинамического торможения, описывается выражением:
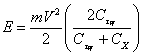 , (1.1)
, (1.1)
где ![]() - коэффициент аэродинамического сопротивления сил нормального давления;
- коэффициент аэродинамического сопротивления сил нормального давления; ![]() - коэффициент аэродинамического сопротивления вязкого трения газа о поверхность КЛА.
- коэффициент аэродинамического сопротивления вязкого трения газа о поверхность КЛА.
Понятно, что при полете КЛА в плотных слоях атмосферы планеты орбитальная кинетическая энергия аппарата должна полностью трансформироваться в тепловую, поскольку на поверхности планеты ско рость аппарата равна нулю.
Как следует из выражения (1.1), доля теплоты, затраченная на нагрев конструкции КЛА, зависит от его геометрии. Чем больше ![]() , тем меньшая доля теплоты Е будет подводиться к поверхности аппарата. Это наглядно иллюстрируется данными, представленными на рис. 1 /2/. Видно, что форма спускаемого аппарата (параметр В) сильно влияет на его нагрев, что, в конечном счете, определяет схему и массу тепловой защиты КЛА.
, тем меньшая доля теплоты Е будет подводиться к поверхности аппарата. Это наглядно иллюстрируется данными, представленными на рис. 1 /2/. Видно, что форма спускаемого аппарата (параметр В) сильно влияет на его нагрев, что, в конечном счете, определяет схему и массу тепловой защиты КЛА.
Однако параметр Е нельзя считать единственным критерием, обусловливающим эффективность тепловой защиты. Определяющими, в этом смысле, процессами являются перенос теплоты и массы в пограничном слое, а также переизлучения энергии поверхностью КЛА в открытое пространство. Кроме того, материалы в составе тепловой защиты, имеют различные теплозащитные и теплофизические свойства. В итоге, совокупность всех этих факторов определяет способность тепловой защиты воспринимать, рассеивать и переда вать определенную (расчетную) долю теплоты в объем КЛА. Эти свойства обеспечивают надежность тепловой защиты в смысле сохранения целостности аппарата в течения всего срока выполнения поставленной программы. Поэтому проектирование тепловой защиты охватывает комплекс задач, главной из которых является задача расчета теплообмена на всей траектории входа аппарата в плотные слои. Конечная цель сводится к установле нию закона изменения плотности конвективного теплового потока в конструкцию аппарата по времени полета. Без этих данных невозможно выбрать оптимальную структурную схему теплозащиты, рассчитать температуру ее поверхности, а, следовательно, оценить работоспособность и надежность всей системы.
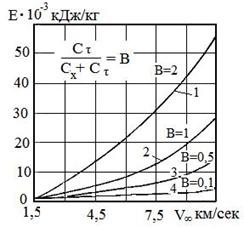
Рис. 1. Изменение удельной энергии, подводимой к килограмму массы конструкции КЛА, в зависимости от скорости полета. 1 – полный переход кинетической энергии в тепловую, 2 – КЛА конической формы, притупленные сферой, 3 – схемы КЛА самолетного типа, 4 – КЛА сферической формы.
Кроме того, необходимость такого анализа обусловлена излучением нагретой поверхностью КЛА части энергии (излучательные свойства), а также особенностями конвективного теплообмена в химически активном пограничном слое. Как известно, интенсивность такого теплообмена на значительном участке траектории полета КЛА зависит от каталитической активности материала тепловой защиты по отношению к реакции гетерогенной рекомбинации ато мов (каталитические свойства). Ниже проводится такой анализ.
1. Процессы тепло - и массообмена на поверхности КЛА.
Впервые влияние на теплообмен ламинарного химически активного пограничного слоя, возникающего на поверхности КЛА при входе в плотные слои атмосферы проанализирован в работах /3,…7/.
Теоретически, а затем и экспериментально установлено, что тепловой поток к поверхности в отсутствие химического равновесия сильно зависит от кинетики процессов рекомбинации как в объеме по граничного слоя, так и на поверхности КЛА. Этот эффект особенно значителен для течений раз реженного газа, когда числа Кнудсена достаточно велики. В этом случае, по мере полета КЛА по траектории, сначала исчезает невязкий слой. Затем вязкий слой у поверхности тела сливается с ударной волной, образуя вязкий непрерывный сжатый слой между поверхностью спускаемого аппарата и ударной волной. В таком слое плотность газа столь низкая, что молекулы компонентов воздуха, проходя через ударную волну и сжатый слой, диссо циируют на атомы, которые диффундирует к поверхности в объеме вязкого пограничного слоя. Для такого режима течения вероятность столкновения частиц очень мала, что исключает процесс рекомбинации атомов в объеме слоя. Такой пограничный слой называется «замороженным». В «замороженном» слое тепловой поток в стенку определяется как интенсивностью процесса диффузии атомов к поверхности, так и реакцией рекомбинации атомов на поверхности теплозащитного покрытия. Как отмечалось, скорость этой реакции сильно зависит от каталитической активности материала на поверхности КЛА.
Таким образом, тепло обмен в «замороженном» пограничном слое на поверхностях с разной каталитичес кой активностью, сильно отличается по интенсивности. Сегодня, этому вопросу уделяется большое внимание в связи с разработкой КЛА нового поколения. Проведены многочисленные теоретические и экспериментальные исследования /8/, в том числе и исследования данной работы.
Химическое состояние воздуха в объеме пограничного слоя гиперзвукового аппарата определяется распределением параметров состояния - температуры, Т и давления, р в его объеме /9, 10/. Уровень этих параметров каждой локальной точке слоя устанавливает закон распределения концентраций атомов и молекул. В итоге, воздух становится многокомпонентной смесью. Одной из характеристик такого газа является массовая концентрация частиц, которая определяется как:
![]() , (1.2)
, (1.2)
где r и ri – средняя плотность смеси компонентов воздуха и плотность каждой i-ой компоненты (например, атомов) в пограничном слое, соответственно. Компонентный состав воздуха в пограничном слое устанавливается скоростью химических реакций, которые протекают в нем. Такими реакциями для воздуха являются реакции диссоциации молекул кислорода и азота и рекомбинации их атомов. Таким образом, при значительных уровнях температуры и умеренных давлениях торможения (например, Т0 ³ 5000К, р0 > 105 Па) в общем двухкомпонентный воздух становится многокомпонентным (О2, О, N2, N и NO). Наличие в пограничном слое химических реакций вызывает дополнительное выделение или поглощение теплоты как в объеме слоя (эндотермические реакции диссоциации молекул), так и на поверхности КЛА (экзотермические реакции рекомбинации атомов).
Этот процесс вносит заметный вклад в теплообмен между газовой фазой и стенкой. Поэтому при составлении математической модели с целью решения задачи тепло - массообмена в химически активном пограничном слое приходится кроме совокупности дифференциальных уравнений неразрывности, движения, энергии и концентрации решать уравнения кинетики, описывающие условия протекания химических реакций. При этом, следует помнить, что все теплофизические свойства и коэффициенты переноса теплоты и массы, такие как: плотность r, удельная изобарная теплоемкость Ср, динамическая вязкость m, теплопроводность l, коэффициент концентрационной диффузии ![]() и другие зависят от температуры, давления и компонентного состава смеси. Решение такой математической модели многокомпонентного пограничного слоя вызывают определенные трудности /3,5/. Это обусловливается рядом причин. Например, одной из таких причин является низкая достоверность определения коэффициентов переноса и потенциалов взаимодействия между частицами. Другая причина выражается в использовании недостаточно точных уравнений кинетики химических реакций. Вот почему все расчеты даже в случае самого простого ламинарного режима течения в пограничном слое необходимо обязательно сопоставлять с экспериментальными данными.
и другие зависят от температуры, давления и компонентного состава смеси. Решение такой математической модели многокомпонентного пограничного слоя вызывают определенные трудности /3,5/. Это обусловливается рядом причин. Например, одной из таких причин является низкая достоверность определения коэффициентов переноса и потенциалов взаимодействия между частицами. Другая причина выражается в использовании недостаточно точных уравнений кинетики химических реакций. Вот почему все расчеты даже в случае самого простого ламинарного режима течения в пограничном слое необходимо обязательно сопоставлять с экспериментальными данными.
Из химической термодинамики известно, что течение химических реакций может происходить как равновесно, так и не равновесно. Определим состояние химических реакций, используя символику реакции, в виде:
![]() , (1.3)
, (1.3)
![]() . (1.4)
. (1.4)
Записанные в символах реакции означают, что реакция (1.3) – прямая, ее константа скорости ![]() , в то время как реакция (1.4) обратная, ее константа скорости
, в то время как реакция (1.4) обратная, ее константа скорости ![]() . Если
. Если ![]() , то такая реакция называется равновесной, а пограничный слой, в котором все реакции протекают равновесно, называется химически равновесным. Если константа скорости
, то такая реакция называется равновесной, а пограничный слой, в котором все реакции протекают равновесно, называется химически равновесным. Если константа скорости ![]() , то такая реакция называется химически неравновесной. Пограничный слой, представляющий собой совокупность нескольких неравновесных реакций, называется химически неравновесным.
, то такая реакция называется химически неравновесной. Пограничный слой, представляющий собой совокупность нескольких неравновесных реакций, называется химически неравновесным.
Неравновесные пограничные слои образуются на поверхности космических летательных аппаратов, когда газ находится в разреженном состоянии, т.е. на значительных высотах полета. В этом случае длина свободного пробега частиц существенная, в результате процесс их взаимодействия в объеме пограничного слоя таков, что реакция диссоциации молекул протекает с большей скоростью, чем обратная реакция, реакция рекомбинации. В принятой символике это означает, что К1 > К2.
При значительном разряжении газа (низкое статическое давление), когда частицы практически не взаимодействуют друг с другом, химические реакции в пограничном слое не протекают. Такие условия реализуются при полете космических летательных аппаратов в верхних слоях атмосферы. Как отмечалось, такой пограничный слой называется «замороженным». Возможные режимы течений (химические состояния пограничных слоев) в зависимости от высоты и скорости полета космических летательных аппаратов приведены на рис. 2 /8/.
Из представленных на рисунке данных следует, что в зависимости от выполняемой задачи, полет аппарата при входе в атмосферу может длительно протекать в зонах либо «замороженного», либо неравновесного, либо равновесного течений.
Н, км
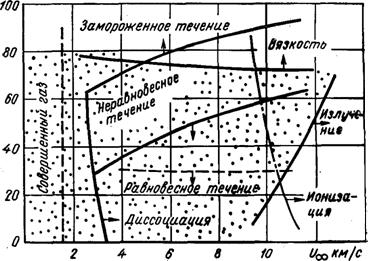
Рис. 2. Возможные химические состояния пограничных слоев (режимы течения) в зависимости от высоты и скорости полета космического аппарата. Расчет для сферы с радиусом, R=1 м. Область влияния вязкости и излучения на режимы течения заштрихована /9/
Так как траектория полета КЛА планирующего класса в атмосфере пологая (несколько тысяч секунд), то время прохождения аппарата каждой из указанных зон оказывается весьма длительным. Это значит, что аэродинамический нагрев КЛА будет сильно зависеть от химического состояния пограничного слоя, которое, как отмечалось, определяется режимом течения. В этой связи, целесообразно провести оценку влияния на теплообмен химического состояния пограничного слоя.
На первом этапе анализа ограничимся рассмотрением двух предельных случаев – «замороженного» и равновесного пограничных слоев, образованных на плоской поверхности. Как отмечено в работах /5, 9, 10/, во всех указанных случаях процессы тепло - и массообмена в пограничном слое определяются теплопроводностью, конвекцией и диффузией в виде:
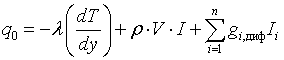 . (1.5)
. (1.5)
При этом задача массопереноса решается с использованием закона Фика и уравнения массовой концентрации i-ой компоненты в виде:
- диффузионный поток массы i-ой компоненты (закон Фика):
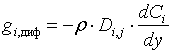 ; (1.6)
; (1.6)
- уравнение массовой концентрации i-oй:
![]() . (1.7)
. (1.7)
В случае, когда пограничный слой «замороженный» скорость образования i-го компонента в объеме слоя ![]() = 0. Тогда уравнение (1.7) будет описывать распределения массовой концентрации i-го компонента по толщине многокомпонентного химически не реагирующего пограничного слоя. Такой пограничный слой назовем первым из возможных предельных вариантов.
= 0. Тогда уравнение (1.7) будет описывать распределения массовой концентрации i-го компонента по толщине многокомпонентного химически не реагирующего пограничного слоя. Такой пограничный слой назовем первым из возможных предельных вариантов.
Кроме отмеченного варианта, возможен другой предельный вариант пограничного слоя, когда скорости химических реакций в объеме слоя бесконечно велики (![]() ) по сравнению со скоростями диффузии каждой
) по сравнению со скоростями диффузии каждой
i-ой компоненты. В этом случае массовые концентрации Сi всех i-ых компонентов в каждой локальной точке пограничного слоя не зависят от процесса диффузии, а будут определяться химическим равновесием, т.е. будут зависеть только от температуры и давления. Такой вариант пограничного слоя получил наименование равновесного пограничного слоя.
Понятно, что кроме указанных двух предельных вариантов, возможен еще один средний, промежуточный вариант, в котором химические реакции протекают неравновесно.
По своей физико-химической природе все указанные варианты пограничных слоев заметно разнятся, поэтому интенсивность тепло – и массообмена в них будет разная, что необходимо учитывать при решении задачи теплоотдачи на поверхности КЛА.
2. Тепло – и массообмен в химически активном пограничном слое на каталитически активной поверхности.
Как известно, явление катализа весьма распространено в химической кинетике. Поскольку в рассматриваемом нами случае пограничный слой является химически активным, то, очевидно, и в нашем случае можно использовать явление катализа в качестве средства управления процессами тепло – и массообмена на поверхности КЛА /8/. Для более полного понимания такой возможности, рассмотрим весь механизм переноса теплоты и массы как в объеме пограничного слоя, так и у поверхности тела.
Известно, что при гиперзвуковом полете КЛА в ударной волне и сжатом слое протекают реакции диссоциации молекул газа набегающего потока. Для простоты анализа, рассмотрим вполне реальный режим, когда на внешней границе пограничного слоя газ набегающего потока полностью диссоциированный. Температура атомарной газовой смеси вследствие теплообмена, по мере приближения к относительно холодной поверхности КЛА, уменьшается, что должно привести к рекомбинации атомов в молекулы. Интенсивность этого процесса будет определяться как химическим состоянием пограничного слоя, так и каталитической активностью материала стенки к реакции рекомбинации атомов.
Проанализируем процесс переноса теплоты и массы для случая первого предельного варианта пограничного слоя, когда химические реакции в нем «заморожены». В таком случае, атомы по мере диффузии к поверхности не будут успевать рекомбинировать в молекулы в объеме пограничного слоя. Достигнув поверхности, химически активные атомы могут реализоваться в трех потенциальных вариантах:
- реагируют с материалом поверхности, если последний имеет химическое сродство к атомарным компонентам. Этот вариант не пригоден для тепловой защиты КЛА планирующего класса, поскольку тепловая защита таких аппаратов должна быть неразрушаемой, многоразовой;
- не реагируют, если материал поверхности химически нейтрален к атомарным компонентам, но является катализатором к реакции рекомбинации атомов. В этом случае, на поверхности КЛАреализуется реакция рекомбинации с выделением громадного количества теплоты – теплоты образования молекул. Этот процесс значительно увеличивает плотность теплового потока в конструкцию КЛА, что невыгодно;
- не реагируют с материалом поверхности, при этом материал поверхности не является катализатором (является ингибитором) реакции рекомбинации. В этом случае реакция рекомбинации атомов будут протекать на поверхности замедленно ![]() . Газ в пограничном слое становится атомарным. По толщине слоя градиент массовых концентраций атомов исчезнет. Процесс диффузии атомов в объеме слоя самоликвидируется (в ур. 1.5 диффузионный поток массы атомов к поверхности gi = 0) и перенос теплоты в объеме слоя будет осуществляться только теплопроводностью и конвекцией (1.5).
. Газ в пограничном слое становится атомарным. По толщине слоя градиент массовых концентраций атомов исчезнет. Процесс диффузии атомов в объеме слоя самоликвидируется (в ур. 1.5 диффузионный поток массы атомов к поверхности gi = 0) и перенос теплоты в объеме слоя будет осуществляться только теплопроводностью и конвекцией (1.5).
Просто показать возможный вклад катализатора в теплообмен на примере реакций рекомбинации компонентов высокотемпературного воздуха – атомов кислорода и азота. Например, энтальпии рекомбинации атомов кислорода и азота в молекулы равны:
- атомы кислорода…… h0 O = 1,54∙104кДж/кг ;
- атомы азота…………. h0N = 3,34∙104кДж/кг.
Для сравнения теплота горения углерода в кислороде составляет ![]() .
.
Как видно, вклад гетерогенных реакций рекомбинации атомов в процесс теплообмена при гиперзвуковых скоростях полета КЛА может быть весьма большим и его необходимо учитывать. Для этой цели в последующих разделах ограничимся анализом двух предельных случаев – «замороженного» и равновесного пограничных слоев. Очевидно, результаты оценки теплообмена в случае промежуточного, неравновесного режима будут расположены в промежутке между значениями указанных предельных режимов.
На первом этапе, для указанных режимов, проанализируем процесс теплообмена в «замороженном» пограничном слое на каталитической и некаталитической стенке. Это позволит сделать некоторые выводы о влиянии каталитических свойств материала стенки на теплообмен.
2.1. Тепло-массообмен в ламинарном «замороженном» пограничном слое при абсолютной каталитической активности поверхности.
Анализ будем проводить на примере плоского ламинарного «замороженного» пограничного слоя в бинарной постановке. Подобная задача решалась в работах /5/ и /6/, но в несколько иной интерпретации.
Как отмечалось ранее, в таком пограничном слое скорость образования всех i-ых компонентов ωi = 0, и только на холодной каталитической стенке будет протекать реакция рекомбинации атомов азота и кислорода в соответствующие молекулы. Образовавшиеся при этом молекулы будут поступать в пограничный слой, диффундируя на встречу атомам к внешней границе пограничного слоя. Математическая модель плоского пограничного слоя при Pr = 1 и Le = 1 имеет вид /6/:
- уравнение неразрывности:
![]() ; (2.1)
; (2.1)
- уравнение движения:
![]() ; (2.2)
; (2.2)
- уравнение энергии:
![]() ; (2.3)
; (2.3)
- уравнение диффузии:
![]() . (2.4)
. (2.4)
Запишем уравнения (2.1)…(2.4) в безразмерном виде для чего введем новые переменные:
- безразмерная скорость,
![]() ; (2.5)
; (2.5)
- безразмерная энтальпия,
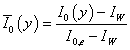 ; (2.6)
; (2.6)
- безразмерная массовая концентрация
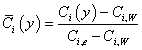 . (2.7)
. (2.7)
Тогда ур. 2.2, 2.3 и 2.4 принимают вид:
![]() , (2.8)
, (2.8)
![]() , (2.9)
, (2.9)
![]() . (2.10)
. (2.10)
Для упрощения дальнейшего анализа воспользуемся аналогией Рейнольдса, согласно которой безразмерные профили (2.5)…(2.7) подобны в пограничном слое при условии, что Pr = 1 и Le = 1.
Проведя далее несложные выкладки, широко используемые при анализе теплообмена в плоском пограничном слое /6/, получим:
![]() , (2.11)
, (2.11)
Воспользуемся далее методом «приведенной» энтальпии /9/ для решения уравнения движения, получим:
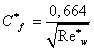 , (2.12)
, (2.12)
где индекс «*» означает, что значение данного параметра рассчитывается для «приведенной» энтальпии, т.е.:
![]() , (2.13)
, (2.13)
I0 – энтальпия адиабатического торможения потока, Iе - энтальпия восстановления адиабатически заторможенного потока, Iw - энтальпия газа набегающего потока при температуре стенки.
В таком случае, формула (2.12) может быть преобразована к виду:
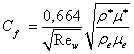 . (2.14)
. (2.14)
Выражения для ![]() и Re, общепринятые /10/. Подставив (2.14) в (2.11) получим:
и Re, общепринятые /10/. Подставив (2.14) в (2.11) получим:
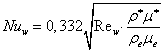 . (2.15)
. (2.15)
Как известно /9, 10/, для рассматриваемого случая конвективный тепловой поток в непроницаемую стенку определяется модифицированным уравнением Ньютона в виде:
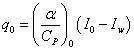 . (2.16)
. (2.16)
Преобразовав (2.15), просто получить выражение для расчета плотности теплового потока в точке торможения КЛА при абсолютно каталитической поверхности в случае «замороженного» пограничного слоя:
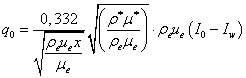 . (2.17)
. (2.17)
Напомним, что мы анализируем случай, когда молекулярные компоненты воздуха (молекулы кислорода и азота) на внешней границе пограничного слоя полностью диссоциированы. В таком случае, энтальпия торможения потока на внешней границе пограничного слоя может быть представлена в виде:
![]() , (2.18)
, (2.18)
где, как и ранее, индекс «е» означает, что данный параметр берется на внешней границе пограничного слоя, ![]() - энтальпия образования атомов. Индекс «i» означает – атомы.
- энтальпия образования атомов. Индекс «i» означает – атомы.
С другой стороны, энтальпию торможения набегающего на КЛА гиперзвукового потока можно записать в виде:
![]() . (2.19)
. (2.19)
Очевидно, ![]() - закон сохранения энергии.
- закон сохранения энергии.
При абсолютной каталитической активности холодной стенки (Тw << T0), все атомы, достигнув ее поверхности, рекомбинируют в молекулы. В таком случае, массовая концентрация атомов на поверхности будет равна нулю и энтальпия воздуха при температуре стенки принимает вид:
![]() , (2.20)
, (2.20)
где индекс «j» означает – молекулы.
Подставив (2.20) в (2.17), окончательно получим:
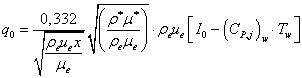 . (2.21)
. (2.21)
Выражение (2.21) позволяет рассчитать плотность теплового потока в стенку КЛА при ее абсолютной каталитической активности.
При этом, оценка для расчета параметров, выделенных знаком «*» в формуле (2.21) проводится с использованием величины «приведенной» энтальпии I* (выражение 2.13), которая для рассматриваемого случая принимает вид:
![]() . (2.22)
. (2.22)
2.2. Тепло-массообмен в ламинарном «замороженном» пограничном слое при нулевой каталитической активности поверхности.
В данном, как и в предыдущем случае, реакции рекомбинации атомов в объеме пограничного слоя протекать не будут, поскольку пограничный слой «заморожен». Так как стенка является ингибитором для реакции рекомбинации (каталитическая активность стенки равна нулю), то на ее поверхности эта реакция будет также «заморожена». Тогда компонентный состав пограничного слоя будет включать только атомы, в нашем случае атомы кислорода и азота.
Тогда энтальпия газа Iw при температуре стенки будет иметь другую величину, чем в предыдущем случае, а именно:
![]() , (2.23)
, (2.23)
где hi0 – теплота образования i-го атома.
Далее, следуя, как и ранее, методу «приведенной» энтальпии, просто получить формулу для расчета плотности теплового потока при нулевой каталитической активности стенки, т.е.:
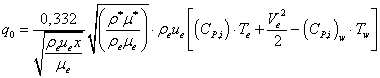 . (2.24).
. (2.24).
Значение «приведенной» энтальпии, как и в предыдущем случае, будем рассчитывать по формуле:
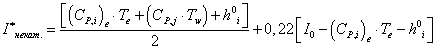 . (2.25)
. (2.25)
Сопоставив формулы (2.21, 2.22) и (2.24, 2.25) видим их заметное различие.
2.3. Анализ влияния каталитических свойств поверхности на теплообмен в «замороженном» пограничном слое
Проведем сравнительный анализ результатов, полученных в разделах 2.2 и 2.3. Для этого сопоставим величины тепловых потоков в каталитическую и некаталитическую стенку. Имеем:
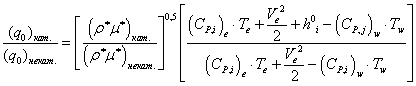 . (2.26)
. (2.26)
Преобразуем (2.26) при следующих приближениях:
- удельные изобарные теплоемкости ![]() и
и ![]() различаются не очень сильно, поскольку
различаются не очень сильно, поскольку ![]() , а также, что
, а также, что ![]() ;
;
- ![]() ;
;
- ![]() .
.
С учетом указанного, выражение (2.26) принимает вид:
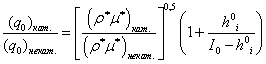 . (2.27)
. (2.27)
Как отмечалось, параметры ![]() в случае каталитической стенки определяются величиной «приведенной» энтальпии согласно (2.22), которое с учетом принятых допущений принимает вид:
в случае каталитической стенки определяются величиной «приведенной» энтальпии согласно (2.22), которое с учетом принятых допущений принимает вид:
![]() . (2.28)
. (2.28)
Те же параметры для некаталитической стенки определяются величиной «приведенной» энтальпии, в виде:
![]() . (2.29)
. (2.29)
Таким образом, используя (2.28) и (2.29), просто получить, что:
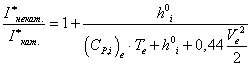 . (2.30)
. (2.30)
Как видно, второй член выражения меньше единицы и, следовательно, различие между ![]() и
и ![]() не велико. Поэтому предельный диапазон изменения левой части (2.30) составляет:
не велико. Поэтому предельный диапазон изменения левой части (2.30) составляет:
![]() . (2.31)
. (2.31)
Оценим далее значение комплекса 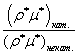 в выражении (2.27) с учетом полученного диапазона изменения (2.31).
в выражении (2.27) с учетом полученного диапазона изменения (2.31).
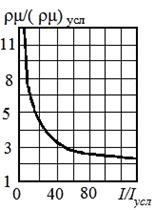
Рис. 3. Зависимость безразмерного комплекса ![]() от безразмерной энтальпии
от безразмерной энтальпии
![]() ;
; ![]() ;
; ![]()
Для этого обратимся к зависимости 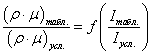 , построенной с использованием табличных данных и представленной для высокотемпературного воздуха на рис. 3. Видно, что в области больших значений Iтабл., что соответствует реальному полету КЛА в атмосфере, рассматриваемая функциональная зависимость выполаживается, т.е. слабо зависит от изменения энтальпии, асимптотически приближаясь к единице. Поэтому в нашем случае, в первом приближении, можно принять, что
, построенной с использованием табличных данных и представленной для высокотемпературного воздуха на рис. 3. Видно, что в области больших значений Iтабл., что соответствует реальному полету КЛА в атмосфере, рассматриваемая функциональная зависимость выполаживается, т.е. слабо зависит от изменения энтальпии, асимптотически приближаясь к единице. Поэтому в нашем случае, в первом приближении, можно принять, что
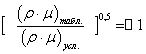 . (2.32)
. (2.32)
Таким образом, с учетом приведенного анализа выражение (2.27) принимает вид:
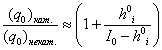 . (2.33)
. (2.33)
Выражение (2.33) весьма приближенно отражает истинное состояние вопроса, поскольку она выведено для однородного по химическому составу атомарного газа в пограничном слое. Например, для оценки влияния на теплообмен каталитической активности поверхности при полете КЛА в земной атмосфере, данное выражение можно применять только полной диссоциации молекул кислорода воздуха, так как при наличии процесса диссоциации молекул азота, атомарный газ в пограничном слое становится неоднородным, что не учитывается выражением (2.33).
Проведем такую оценку на простом примере. Рассмотрим случай, когда на внешней границе пограничного слоя кислород находится в атомарном состоянии, т.е. полностью диссоциирован. Из химической термодинамики известно, что условие реализации этого процесса определяется давлением и температурой. Например, если давление на внешней границе пограничного слоя будет составлять Рв = 105Па, то полная диссоциация молекул кислорода наступит при температуре, равной Тв = ~ 5000К. Как известно, при указанных параметрах процесс диссоциации молекул азота только начинается. Все эти особенности продемонстрированы на рис. 4.
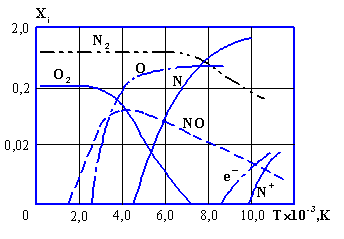
Рис. 4. Мольные доли компонентов воздуха при химическом равновесии смеси в зависимости от температуры при ρ/ρo = 1: /10/. ρo = 1,293 кг/м3 – плотность воздуха при нормальных условиях: То = 273 К, pо = 105 Па; e- – мольная доля электронов; N+– мольная доля ионов азота. Мольные доли, ![]() ,
, ![]() и
и ![]() - число молей
- число молей ![]() компонента и смеси (воздуха), соответственно.
компонента и смеси (воздуха), соответственно.
Пусть полет КЛА происходит на высоте Н = 75км со скоростью, соответствующей числу Маха, М = 23. Параметры атмосферы на данной высоте составляют: ТН = 203К, РН = 2,64Па. В таком случае энтальпию торможения набегающего потока можно рассчитать по известной формуле:
![]() . (2.34)
. (2.34)
При k = 1,4 и изобарной теплоемкости воздуха ![]() просто рассчитать, что
просто рассчитать, что ![]() . При этом давление торможение набегающего потока составит
. При этом давление торможение набегающего потока составит![]() .
.
Как известно, энергия диссоциации молекул кислорода составляет ![]() . Тогда, согласно (2.33), получаем, что
. Тогда, согласно (2.33), получаем, что ![]() .
.
Таким образом, из проведенного анализа следует, что плотность теплового потока в стенку при ламинарном «замороженном» диссоциированном пограничном слое сильно зависит от каталитической активности поверхности. Таким свойством может обладать материал теплозащитного покрытия. Поэтому, при проектировании системы тепловой защиты КЛА планирующего класса, этому вопросу следует уделять самое пристальное внимание.
2.4. Анализ влияния каталитических свойств поверхности на теплообмен в ламинарном равновесном пограничном слое.
Как отмечалось ранее, в случае равновесного пограничного слоя в каждой локальной точке его объема имеет место химическое равновесие как прямой реакции (реакции диссоциации), так и обратной (реакции рекомбинации). Скорость образования всех i-ых (атомов) и всех j-ых (молекул) компонентов бесконечно велика, ![]() . При такой громадной скорости реакций, каталитические свойства материала поверхности не могут оказывать какое-нибудь влияние на интенсивность этих реакций. Поэтому компонентный состав газа и в пограничном слое, и на поверхности будет определяться только уровнем температуры и давления в каждой локальной точке.
. При такой громадной скорости реакций, каталитические свойства материала поверхности не могут оказывать какое-нибудь влияние на интенсивность этих реакций. Поэтому компонентный состав газа и в пограничном слое, и на поверхности будет определяться только уровнем температуры и давления в каждой локальной точке.
Для дальнейшего анализа воспользуемся методом «приведенной» энтальпии и получим формулу для расчета плотности теплового потока. Так как в случае равновесного пограничного слоя каталитичность поверхности не влияет на ход реакций диссоциации и рекомбинации, то формула для расчета теплового потока принимает вид:
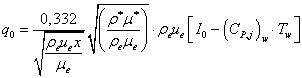 . (2.35)
. (2.35)
При выводе формулы было принято, что ![]() , а также, что массовая концентрация атомов на поверхности
, а также, что массовая концентрация атомов на поверхности ![]() и массовая концентрация молекул на поверхности
и массовая концентрация молекул на поверхности ![]() . Как и ранее, значения параметров
. Как и ранее, значения параметров ![]() и
и ![]() определяются с использованием величины «приведенной» энтальпии, т.е.:
определяются с использованием величины «приведенной» энтальпии, т.е.:
![]() . (2.36)
. (2.36)
Проведем далее сравнение тепловых потоков в стенку при ее абсолютной каталитичности для случаев равновесного и «замороженного» пограничных слоев. Очевидно, для этих условий имеем:
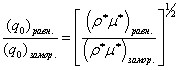 . (2.37)
. (2.37)
Поскольку значения ![]() и
и ![]() определяются с использованием выражения (2.36), которое справедливо как для равновесного, так и «замороженного» пограничных слоев, то, очевидно:
определяются с использованием выражения (2.36), которое справедливо как для равновесного, так и «замороженного» пограничных слоев, то, очевидно:
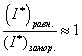 . (2.38)
. (2.38)
Тогда из (2.37) следует, что:
![]() . (2.39)
. (2.39)
Итак, на основании проведенного выше сравнительного анализа можно сделать вывод о том, что в двух предельных случаях «замороженного» и равновесного пограничных слоев тепловой поток в абсолютно каталитическую стенку одинаков. Это значит, что при абсолютной каталитической активности поверхности КЛА тепловой поток в стенку, обтекаемую диссоциированным газом, практически не зависит от степени неравновесности пограничного слоя.
Обобщая результаты анализа, проведенного в данном разделе, можно отметить, что процессы тепло – и массообмена на поверхности КЛА планирующего класса в сильной степени определяется химическим сродством материалов теплозащитного назначения к реакции поверхностной рекомбинации атомов набегающего потока. Это выдвигает определенные научно обоснованные требования, которые необходимо выполнять при проектировании тепловой защиты для аппаратов такого класса. Суть этих требований заключается в том, что при полете КЛА на больших высотах
(60...90км), когда пограничный слой на поверхности неравновесный, каталитическая активность материала теплозащитного покрытия (ТЗП) может играть решающую роль в процессе тепло и массообмена. В этой связи при проектировании системы тепловой защиты необходимо располагать широким спектром ТЗМ разной каталитической активности, чтобы управлять скоростью поверхностной рекомбинации атомов диссоциированного потока.
3. Роль излучательной способности поверхности в системах тепловой защиты КЛА
Излучательная способность, как оптическая характеристика материалов тепловой защиты, является важным параметром, определяющим условия теплового баланса на по верхности систем тепловой защиты КЛА планирующего класса. Поэтому можно смело утверждать, что излучательная способность тепловой защиты является единственным фактором, позволяющим управлять условием теплового баланса на по верхности КЛА такого класса. Как известно /6/, интенсивность излучения твердых тел подчиняется закону Стефана-Больцмана в виде:
![]() , (3.1)
, (3.1)
где qизл. – лучистый тепловой поток, излучаемый в пространство поверхностью тепловой защиты КЛА, с температурой Тw, εw – степень черноты поверхности, σ – коэффициент излучения черного тела.
Для КЛА планирующего класса условие теплового баланса на по верхности тепловой защиты составляется из положения, что плотность конвективного теплового потока qкон, подведенного к поверхности, равна плотности лучистого теплового потока qизл , излучаемого поверхностью в открытое пространство. В математической форме уравнение баланса имеет вид:
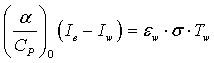 . (3.2)
. (3.2)
При выполнении указанного баланса Tw называют равновесной температурой, которая определяется для каждого выделенного элемента поверхности тепловой защиты КЛА. При этом плотность конвективного теплового потока, равная  , рассчитывается с использованием теории химически активного пограничного слоя на траектории полета для всех выделенных элементов на поверхности КЛА /10/.
, рассчитывается с использованием теории химически активного пограничного слоя на траектории полета для всех выделенных элементов на поверхности КЛА /10/.
Из (3.2) видно, что управлять величиной плотности теплового потока, излучаемого поверхностью ТЗП, можно только с помощью двух параметров, либо коэффициентом черноты поверхностиεw, либо температурой поверхности Tw. Из уравнения баланса тепловых потоков (3.2) следует, что как степень черноты поверхности εw системы тепловой защиты, так и ее температура Тw, в реальном полете должны принимать максимально возможные значения.
Заключение
Таким образом, из проведенного анализа становится очевидным, что каталитические и излучательные свойства ТЗП являются одними из важнейших свойств в системах тепловой защиты КЛА планирующего класса.
Кроме того, из проведенного анализа следует, что характеристики систем тепловой защиты КЛА и ее надежность определяется максимально возможными уровнями степени черноты поверхности εw и ее температуры Тw минимальной каталитической активности материала. В этой связи для разработки КЛА нового поколения научное прогнозирование композиционного состава ТЗМ с целью улучшения их свойств является важнейшей задачей высокотемпературной теплотехники и материаловедения.
Работа выполнена при поддержке Российского фонда фундаментальных исследований по проекту 06-08-00184-a.
СПИСОК ЛИТЕРАТУРЫ
1. «Основы теории полета космических аппаратов» / под ред. Г.С. Нариманова и М.К. Тихонравова. М., «Машиностроение», 1972, с. 539-559.
2. Полежаев Ю.В., Юревич Ф,Б. «Тепловая защита» / под ред. А.В. Лыкава. М.: «Энергия» 1976. 392 с.
3. Фей Дж., Ридделл Ф. «Теоретический анализ теплообмена в лобовой точке, омываемой диссоциированным воздухом». – В кн. «Проблемы движения головной части ракет дальнего действия» М., Изд. «ИЛ», 1959,
с. 217-256.
4. Гулард Р. О влиянии скоростей каталитической рекомбинации на теплопередачу при торможении гиперзвукового потока // Вопросы ракетной техники, 1959, № 5, с.3-23.
5. Анфимов Н.А. «Ламинарный пограничный слой на химически активной поверхности». – «Известия АН СССР, ОТН, Механика и машиностроение», 1962, № 3, с. 46-52.
6. Анфимов Н.А. «Ламинарный пограничный слой в многокомпонентной смеси газов». – «Известия АН СССР, ОТН, Механика и машиностроение». 1962, №1,С. «5…31.
7. Агафонов В.П., Вертушкин В.К., Гладков А.А., Полянский О.Ю. Неравновесные физико-химические процессы в аэродинамике. М., «Машиностроение», 1972, 344 с.
8. Ковалев В.Л. «Гетерогенные каталитические процессы в аэродинамике». – М.: ФИЗМАТЛИТ, 2002. – ISBN 5-9221-0198-6.
9. Авдуевский В.С., Галицейский Б.М., Данилов Ю.И. и др. « Основы теплопередачи в авиационной и ракетно-космической технике» / под общ. ред. В.С. Авдуевского, В.К. Кошкина. 2-е изд. – М., «Машиностроение», 1992, 528 с.
10. Никитин П.В. «Тепловая защита», Учебник высшей школы. М.: 2006. 610 с.



