Подготовка команды для участия во Всеармейской олимпиаде - длительный и трудоемкий процесс, который осуществляется в несколько этапов. На первом этапе проводится математическая олимпиада среди обучающихся института, по результатам которой осуществляется набор в группу подготовки к Всеармейской олимпиаде. Второй этап состоит в подготовке отобранных обучающихся по различным темам курса «Математика». К этим темам относятся следующие:
-
линейная алгебра;
-
аналитическая геометрия;
-
введение в математический анализ;
-
дифференциальное и интегральное исчисление;
-
дифференциальные уравнения;
-
ряды.
Как известно из методической литературы, все задания курса «Высшая математика» подразделяются на четыре уровня.
Первый уровень. Для него характерно овладение отдельно взятым действием.
Второй уровень. Его содержание составляет овладение более сложным действием, составленным из нескольких действий, и способность применения сложного действия в алгоритмической ситуации.
Третий уровень. Характеризуется овладением сложным действием, способностью применения этого действия вне алгоритмических ситуаций.
Четвертый уровень. Его содержание составляет способность применения сложного действия вне алгоритмических ситуаций, а также свободное оперирование действиями, адекватными рассматриваемому понятию.
Очевидно, что задания для подготовки к олимпиаде принадлежат к четвертому уровню овладения действиями. Но и здесь следует выделить несколько видов заданий:
-
на свободное оперирование действиями, необходимыми для выполнения поставленной задачи;
-
на применение сложного действия вне алгоритмических ситуаций.
На примере темы «Аналитическая геометрия» поясним методику подбора задач для подготовки к олимпиаде.
Большинство задач по аналитической геометрии относятся к задачам второго вида, поэтому организация занятий по этой теме является одной из самых сложных. Нами разработаны занятия, которые позволяют классифицировать основные виды задач, предлагаемых на олимпиаде (как показал анализ олимпиадных заданий за последние несколько лет) [1; 2; 5].
Занятия по трем основным темам
-
На геометрическое место точек.
-
На угол между кривыми.
-
На кратчайшее расстояние между кривыми.
Завершением работы по теме «Аналитическая геометрия» является самостоятельная работа следующего содержания.
1. При каких значениях параметра k прямые
![]()
![]()
![]()
пересекаются в одной точке?
2. Найти угол между кривыми:
![]()
3. Найти кратчайшее расстояние между графиками функций:
![]() ,
, ![]()
4. Один конец отрезка перемещается по оси абсцисс, а другой по оси ординат. Найти уравнение линии, описываемой серединой этого отрезка, если длина отрезка l.
5. Найти уравнение траектории точки М, которая движется так, что ее расстояние от точки А(-1;0) вдвое меньше расстояния до прямой х=-4.
Первая задача в самостоятельной работе относится к 1-му типу заданий, т.е. предполагает свободное оперирование действиями, необходимыми для ее решения.
Задачи 2-5, после проведенных занятий с обучающимися, должны из заданий 2-го вида для курсантов при решении стать задачами 1-го вида. Удачное выполнение самостоятельной работы будет свидетельствовать о том, что проведенные занятия цели достигли и обучающиеся свободно оперируют действиями, необходимыми для решения выделенных видов задач по теме «Аналитическая геометрия» [3; 4; 6].
Однако в последнее время наблюдается тенденция к расширению типов задач по теме «Аналитическая геометрия», выносимых на олимпиаду. В 2013 году тема «Аналитическая геометрия» рассматривалась совместно с темами «Определенный интеграл» и «Дифференциальные уравнения». Были выданы задачи следующего вида.
1. Из точек параболы ![]() проводятся касательные к параболе
проводятся касательные к параболе ![]() . Доказать, что площадь криволинейного треугольника, образованного этими касательными и дугой параболы
. Доказать, что площадь криволинейного треугольника, образованного этими касательными и дугой параболы ![]() между точками касания, не зависит от выбора точки на нижней параболе.
между точками касания, не зависит от выбора точки на нижней параболе.
2. Составить дифференциальное уравнение парабол с осью, параллельной оси ![]() , касающихся одновременно прямых
, касающихся одновременно прямых ![]() и
и ![]() .
.
Рассмотрим подробно решение каждой из задач и выделим моменты, на которые особо следует обратить внимание.
Первая задача связана с темой «Определенный интеграл», но для ее решения необходимо вспомнить уравнение касательной к кривой, проведенной в данной точке. Оно будет иметь вид:
![]() , (1)
, (1)
где ![]() ,
,![]() – координаты точки касания. Поскольку касательная проходит через точку A(
– координаты точки касания. Поскольку касательная проходит через точку A(![]() параболы
параболы ![]() то, подставляя ее координаты в уравнение (1), получаем
то, подставляя ее координаты в уравнение (1), получаем
![]() ,
,
а значит, ![]() .
.
Далее переходим непосредственно к теме «Определенный интеграл» и вычисляем искомую площадь криволинейного треугольника ABC, вычитая из площади криволинейной трапеции MBCK, ограниченной параболой
![]() ,
,
![]() , площади трапеций MBAN и NACK, ограниченных касательными и прямыми
, площади трапеций MBAN и NACK, ограниченных касательными и прямыми ![]() (рис. 1).
(рис. 1).
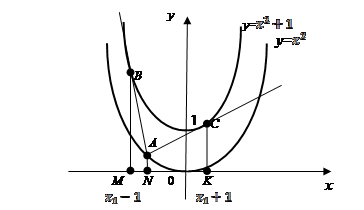
Рис. 1. Схема определения площади криволинейного треугольника ABC.
Получим
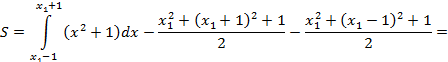
![]() .
.
В итоге мы при вычислении интеграла получили число, а, следовательно, площадь ![]() не зависит от выбора точки
не зависит от выбора точки ![]() .
.
При решении задачи следует актуализировать следующие знания из темы «Аналитическая геометрия»: уравнение касательной к кривой, площади трапеций [7; 8].
При решении второй задачи также необходимо уравнение касательной. Однако, наряду с уравнением касательной, необходимо иметь знания по каноническому уравнению параболы и особенностям этого канонического уравнения в зависимости от расположения кривой. Так, в задаче требуется составить уравнение семейства парабол с осью, параллельной оси ![]() и касающихся прямой
и касающихся прямой ![]() .
.
Это уравнение будет имеет вид ![]() . Для нахождения углового коэффициента касательной продифференцируем полученное уравнение:
. Для нахождения углового коэффициента касательной продифференцируем полученное уравнение:
![]() (2)
(2)
Далее опять же необходимы знания из темы «Аналитическая геометрия», а именно условие касания прямой ![]() вытекает, что
вытекает, что ![]() . Этот факт с учётом формулы (2) даёт
. Этот факт с учётом формулы (2) даёт ![]() , где
, где ![]() и
и ![]() – абсцисса и ордината точки касания соответственно. Отсюда, а также из формулы (2) следует, что:
– абсцисса и ордината точки касания соответственно. Отсюда, а также из формулы (2) следует, что:
![]()
Из последнего равенства получаем
![]() .
.
Подставив значение b в (2) , получим:
![]() ,
,
откуда найдем величину
![]() .
.
Подставив ![]() и
и ![]() в уравнение семейства парабол, получим:
в уравнение семейства парабол, получим:
![]() ,
,
а после преобразований имеем искомое дифференциальное уравнение
![]() .
.
Таким образом, тема «Аналитическая геометрия» являлась в 2013 году базовой при решении задач по интегрированию функций и дифференциальным уравнениям. Особенно необходимы оказались знания по уравнениям касательных, проведенных к графику функций. Таким образом, выделенные в начале статьи типы задач, решаемых при подготовке к Всеармейским олимпиадам, а именно на нахождение угла между кривыми, послужат базой для успешного решения задач по другим разделам олимпиады.
Сама же тема «Аналитическая геометрия» была представлена в этом году следующими задачами.
1. Составить уравнения сторон треугольника, зная одну из его вершин A(4;-1) и уравнения двух биссектрис (![]() .
.
2. Вычислить радиус и координаты центра окружности
![]()
При решении первой задачи необходимо выполнить построение точки, симметричной вершине относительно биссектрисы треугольника. Такое построение никогда раньше нами при подготовке к олимпиаде не рассматривалось, поэтому требуется подбор типов задач на отработку данного действия.
Вторая задача включает в себя знания по взаимному расположению сферы и плоскости. Данный вид задач неоднократно решался при подготовке к олимпиаде, поэтому не является для наших обучающихся новым. Эти задачи включают в себя все основные знания по теме «Аналитическая геометрия» основного курса обучения: уравнение сферы, уравнение плоскости, расстояние от точки до плоскости, параметрические уравнения прямой, направляющий вектор прямой, нормальный вектор плоскости.
Таким образом, при подготовке к Всеармейским олимпиадам по теме «Дифференциальная геометрия» необходимо:
-
Отрабатывать типы задач, выделенные в начале статьи.
-
Уделять должное внимание самостоятельной работе обучающихся по отработке полученных знаний на практике.
-
Включить в план подготовки задачи, находящиеся на стыке нескольких тем курса «Высшая математика».
-
Включить в рассмотрение задачи, при решении которых используется понятие симметрии.
Рецензенты:
Найниш Л.А., д.п.н., профессор, зав. кафедрой «Начертательная геометрия и графика» ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г.Пенза.
Гарькина И.А., д.п.н., профессор, зам. зав. кафедрой «Математика и математическое моделирование», ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.



