Введение
В условиях высокой скорости движения денежных и материальных потоков товаров и услуг большое значение приобретают динамические модели управления запасами компании. Однако данные модели обычно задаются нелинейными системами уравнений или неравенств, и для нахождения оптимального решения требуется качественное техническое и программное обеспечение, а также, в большинстве случаев, оптимальное решение находится исключительно с помощью численных методов решения. Кроме того, стоит отметить узкую направленность практической интерпретации результатов, полученных в ходе решения, и невозможность дальнейшей аналитической работы с ними без соответствующего уровня технической оснащенности.
Решение вышеперечисленных проблем при управлении запасами на производстве с учетом временной составляющей лежит в области применения линейных моделей. Как известно, наиболее эффективным методом нахождения оптимального решения в моделях, заданных линейными системой ограничений и целевой функцией, является симплекс-метод и его модификации. Привлекательность данного метода заключается не только в нахождении точного оптимального решения задачи линейного программирования, но и в параллельном нахождении двойственных оценок переменных модели, практическая интерпретация которых достаточно проста и одновременно довольно информативна с точки зрения управления оборотными активами компании.
В соответствии с вышесказанным предлагается ввести новый тип моделей линейного программирования, который позволил бы представить задачу управления запасами фирмы в динамике. Наиболее просто реализовать такую модель на практике можно, объединив все временные интервалы, на которых будет рассматриваться задача управления запасами. Соответственно предлагаемый способ подразумевает решение одной задачи для двух и более временных интервалов, что, конечно же, отразится на увеличении размерности рассматриваемой задачи, однако, результаты решения будут доступны для практической интерпретации, а сама модель будет универсальной для применения в любых условиях.
Прежде всего, необходимо ввести ряд экономически и практически обоснованных допущений и условий, учет которых позволит описать задачу управления активами в различных временных интервалах с помощью одной целевой функции и единой системы уравнений и/или неравенств.
1. Целевой функцией модели является суммарная чистая прибыль от производственно-коммерческой деятельности компании на всех временных интервалах, которую необходимо максимизировать, причем спрос на продукцию принимается неограниченным, то есть компания всегда может в полном объеме реализовать произведенную продукцию по рыночным ценам в рамках любого временного интервала.
2. Указанный вид целевой функции может привести к случаю, когда в оптимальном решении задачи на одном или нескольких временных интервалах компания не будет ничего производить, однако, на практике такое невозможно. Поэтому в модель целесообразно включить ограничения на объемы производства «снизу», которые на каждом временном интервале обеспечивают минимально допустимую производственную деятельность с целью поддержания функционирования компании.
3. У компании всегда (за исключением первого временного интервала) есть два варианта снабжения собственного производства: приобретение новых ресурсов на рынке, предложение которых для каждого временного интервала ограничено, и использование складских запасов собственных ресурсов.
4. Затраты на хранение ресурсов учитываются как произведение количества ресурсов данного типа на стоимость хранения единицы ресурса указанного типа, в которую включены постоянные издержки. Постоянные издержки хранения в данном случае равномерно распределяются между всеми запасенными ресурсами.
5. Затраты на ресурсы, из которых невозможно сформировать запасы, в модели предлагается учесть путем уменьшения прибыли с единицы произведенной продукции указанного типа, как в целевой функции, так и в системе ограничений.
6. Предложение ресурсов, а также чистая прибыль от продажи продукции компании во всех рассматриваемых временных интервалах считаются известными величинами и могут иметь различные значения в разных временных интервалах.
Отдельно стоит отметить учет использования складских запасов, созданных в прошлом временном интервале, при производстве продукции в настоящий момент. Поскольку основной целью использования описываемой модели является возможность получения двойственных оценок для ресурсов, полученных из разных источников в различных временных интервалах, и которые описывают востребованность каждого конкретного типа ресурса в данный момент времени в зависимости от источника его получения, то в модели необходимо четко разделять ресурсы не только по времени, но и по источнику их получения для производства в заданный момент времени. Однако при изготовлении продукции источник получения ресурса не играет никакой роли с точки зрения производственного процесса, поэтому в модели необходимо рассмотреть все вариации производственных программ, количество которых устанавливается последовательным перебором всех возможных комбинаций снабжения производственного процесса идентичными и полностью взаимозаменяемыми ресурсами, взятыми из различных источников.
Из вышесказанного следует, что в каждый момент времени количество производственных программ для одного вида продукции, обеспечиваемых n-ым количеством типов ресурсов, у которых могут быть различные источники происхождения (предложение ресурса на рынке в данный момент или складские запасы, созданные в прошлом периоде), в соответствии с формулой для вычисления числа размещений с повторениям будет составлять: 
. Для m-го количества типов продукции данное число увеличится соответственно в m-раз.
Таким образом, с учетом всего перечисленного выше, предлагаемая линейная модель динамического управления запасами будет выглядеть следующим образом:
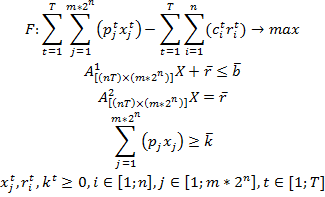
где:
– это количество продукции 
-го вида, изготовленной по 
- производственной программе;
– это чистая прибыль с единицы продукции -го вида, изготовленной по – производственной программе;
– это затраты на хранение единицы ресурса i-го вида, приобретенного в момент времени t;
X – это вектор, описывающий объем производственной продукции по всем типам программ для каждого конкретного временного интервала из рассматриваемого периода;
это производственные матрицы размерности 
которые описывают затраты ресурсов, соответственно привлекающихся на производство из двух различных источников, причем на изготовление каждого вида продукции различным способом. Они имеют блочную структуру, в которой блоки, содержащие ненулевые элементы, лежат на главной диагонали и описывают все производственные программы и затраты ресурсов на каждую из них в конкретном временном интервале;
– вектор размерности [n*T], описывающий предложение i-го ресурса на рынке в момент времени t;
– вектор размерности [n*T], задающий объем запаса i-го ресурса, создаваемого в момент t и доступного к использованию в производстве в момент времени t+1;
– вектор размерности [t], отображающий минимальный размер чистой прибыли компании от производства, необходимого для поддержания работы в момент времени t.
В ходе исследования модели, приведенной выше, определяется вектор X, задающий объемы производства продукции каждого типа по различным производственным программам, вектор , определяющий запасы ресурсов каждого типа, создаваемые в момент времени t и используемые в момент времени t+1, а также вектор двойственных оценок ресурсов – 
, который в некотором интервале устойчивости будет определять увеличение значения целевой функции от увеличения запаса каждого ресурса из каждого источника на 1 ед. Вектор целесообразно разбить на два вектора: 
и 
, которые будут содержать двойственные оценки ресурсов, соответственно, закупаемых на рынке и лежащих на складе. С точки зрения практической интерпретации вектор описывает увеличение прибыли компании от увеличения конкретного типа ресурса с учетом источника его происхождения в любой момент времени, рассматриваемый в модели. Именно координаты вектора делают предлагаемую модель актуальной для использования, поскольку они позволяют учитывать востребованность ресурсов не только в данный момент времени, но и с учетом их завтрашней стоимости, уровня предложения на рынке и ряда иных показателей, которые будут перечислены ниже.
В первую очередь необходимо описать принципы изменения двойственных оценок в зависимости от изменяющихся условий, заданных в модели. Очевидно, двойственные оценки, соответствующие запасам ресурсов в момент t, будут отличны от нуля только в том случае, если сложатся соответствующие экономические условия в моменты времени t-1 и t, к примеру:
- Высокое предложение ресурса i-го типа в момент времени t-1, не позволяющее использовать его в полном объеме в момент времени t-1, а в момент времени t, напротив, предполагается дефицит указанного ресурса, при котором объемы предложения остальных ресурсов окажутся избыточными на производстве;
- Увеличение цены продукции, в изготовлении которой участвует некоторый ресурс i, в момент времени t по сравнению с моментом времени t-1. Очевидно, что увеличение цены должно покрывать затраты на хранение ресурса;
- Увеличение цены единицы ресурса i к моменту времени t, которое опосредованно отразится на размере чистой прибыли (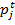), получаемой с продукции, в изготовлении которой принимает участие соответствующий ресурс.
Также возможны иные вариации экономических условий, которые могут быть описаны в приведенной модели, и в которых будет целесообразно создавать запас ресурсов.
Ниже описаны основные принципы изменений значений двойственных оценок, в зависимости от изменений условий модели, и случаи, в которых будет создаваться запас ресурсов. В приведенной модели легко видеть, что при оптимальном решении в отношении двойственных оценок ресурсов всегда будет выполняться неравенство: 
, где 
– это двойственная оценка ресурса i-го типа, закупаемого на рынке в момент времени t, а 
– это двойственная оценка запасов ресурса i-го типа в момент времени t+1. В случаях, когда будет формироваться запас ресурса i, неравенство станет равенством, что легко обосновать с практической точки зрения, так как источником запасов ресурса в момент времени t+1 является предложение данного ресурса на рынке в момент времени t, и, соответственно, если растет востребованность запасов данного ресурса в момент времени t+1, то будет увеличиваться и двойственная оценка закупаемого ресурса в момент времени t. Причем, в случае, если предложение ресурса в момент времени t является избыточным, даже с учетом создаваемого запаса к моменту времени t+1, то двойственная оценка ресурса, приобретаемого на рынке в момент времени t, будет равна нулю и, следовательно, будут иметь место следующие равенства:
при
имеем:
В любом другом случае запасы создаваться не будут, поскольку, согласно значениям двойственных оценок, эффективней будет использовать ресурс непосредственно в момент его покупки на рынке, нежели хранить его в течение некоторого временного интервала за определенную плату.
Для демонстрации принципа работы рассматриваемой модели следует привести пример с конкретными числовыми значениями. Рассмотрим случай, когда фирмой производятся два вида продукции с использованием трех типов ресурсов. Предположим, что нам известно рыночное предложение ресурсов, а чистая прибыль от единицы реализованной продукции в следующем временном интервале останется неизменной. Пусть минимальная сумма чистой прибыли, позволяющая предприятию поддерживать свою деятельность в момент времени t=1, составляет 1500 денежных единиц. Тогда модель управления запасами для двух временных интервалов 
будет иметь следующий вид:
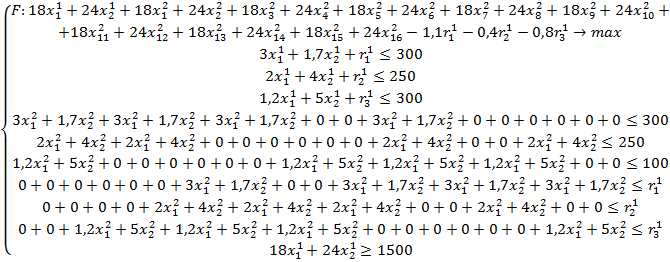
Оптимальное решение данной задачи будет определяться, как было сказано выше, двумя векторами, описывающими объемы производства каждого вида продукции с учетом производственной программы и объемы запасов ресурсов. Данные вектора будут иметь следующие координаты:
Вектора двойственных оценок будут иметь следующий вид:
Как видно из решения задачи, предполагаемый дефицит рыночного предложения ресурса третьего типа в момент времени t=2 можно скомпенсировать созданием запаса в размере 95,35 единиц в момент времени t=1. Также стоит отметить, что размеры и условия рыночного предложения ресурса третьего типа в моменты времени t=1 и t=2 таковы, что востребованность в данном ресурсе, на фоне предложения других ресурсов, для компании равна нулю.
Стоит обратить внимание на тот факт, что при равных размерах чистой прибыли, получаемой в различных производственных программах, то есть, когда мы предполагаем, что цена ресурсов остается неизменной для различных временных интервалов, двойственные оценки для одного типа ресурса, берущегося со склада и закупаемого на рынке, будут равны. Однако, если увеличение запасов ресурса на 1 ед. даст прирост к значению целевой функции не более чем на величину равную 
, то увеличение рыночного предложения того же ресурса на 1 ед. даст прирост целевой функции в размере
, и в этом случае увеличение рыночного предложения в модели приведет к замещению ресурсов, используемых из запасов, на ресурсы, предлагаемые на рынке.
Подводя итоги всего сказанного, можно сделать следующие выводы касательно общей эффективности, актуальности и практического значения использования предлагаемой модели:
- Модель позволяет находить объемы запасов ресурсов различных типов, ориентируясь не только на сложившиеся в данный момент времени экономические условия в сфере деятельности компании, но и опираясь на предполагаемые изменения этих условий в обозримом будущем.
- Набор двойственных оценок, получаемый в ходе нахождения оптимального решения, является удобным и наглядным инструментом для лица, принимающего решение, поскольку он позволяет оценить полезность того или иного ресурса в некотором интервале устойчивости без применения дополнительных и сложных вычислений.
- В указанном виде модель можно использовать для получения практических результатов и оценочных значений, которые позволят составить представление о востребованности ресурсов для компании и объемах предполагаемых запасов ресурсов для использования в будущих периодах.
- Модель имеет потенциал дальнейшего развития. В ней с помощью дальнейших модификаций можно учесть ряд важных факторов, к примеру, факторы временной стоимости денег или ликвидности различных типов ресурсов.
Рецензенты:
Тихомирова Е.И., д.э.н., профессор, декан факультета математической экономики и информатики ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова» Министерства образования и науки РФ, г. Москва.
Татарников О.В., д.т.н., профессор, заведующий кафедрой высшей математики ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова» Министерства образования и науки РФ, г. Москва.