Ядерное квадрупольное, спиновое и световое эхо широко применяются для изучения внутренних движений в кристаллах, природы химической связи, комплексных соединений, дефектов в твердых телах. Эксперименты по ядерному квадрупольному эху, в отличие от экспериментов по обычному ядерному квадрупольному резонансу (ЯКР), позволяют не только получать сведения о константах квадрупольного взаимодействия, параметрах асимметрии и величинах химического сдвига, но и дают возможность исследования неравновесных состояний спин-систем (релаксационные процессы), внутренних электрических и магнитных локальных полей в кристаллах. Импульсные методы ЯКР позволяют наблюдать сигналы в неупорядоченных кристаллах, что существенно расширяет возможности метода.
При исследовании явлений ядерного квадрупольного, спинового и светового эха необходимо решать либо уравнение Шредингера, либо уравнения Блоха. И в том и в другом случае получается система линейных дифференциальных уравнений с переменными коэффициентами (СЛДУПК), решение которой можно представить с помощью мультипликативного интеграла [4]. Точное вычисление мультипликативного интеграла в большинстве случаев затруднительно, но даже использование нулевого приближения для мультипликативного интеграла позволяет получить необходимые аналитические результаты при исследовании явлений эха.
Ранее рядом авторов рассматривались вопросы резонансной обработки сигналов различными методами [2,3]. Одним из важных методов является корреляционная обработка сигнала. В моей работе исследовано влияние наличия помехи на форму эхосигнала в рамках модели Блоха, пригодной для описания спинового и светового эха в парамагнитных материалах.
В данной работе рассмотрено возникновение эха при трехимпульсном воздействии, когда второй сигнал следует за первым через время T3, а третий сигнал следует за первым через время T. Проанализировано стимулированное эхо, возникающее в момент времени ![]() .
.
Для сигнала стимулированного эха получено следующее выражение
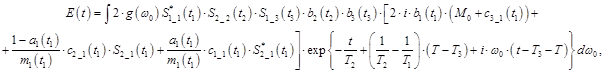 , (1)
, (1)
где
![]()
![]() – текущий спектр сигнала с возрастающей экспонентой,
– текущий спектр сигнала с возрастающей экспонентой,![]() – текущий спектр сигнала с убывающей экспонентой,
– текущий спектр сигнала с убывающей экспонентой, ![]() – радиочастотный сигнал,
– радиочастотный сигнал, ![]() – номер сигнала;
– номер сигнала;
![]() – длительности первого, второго и третьего радиочастотных импульсов;
– длительности первого, второго и третьего радиочастотных импульсов;
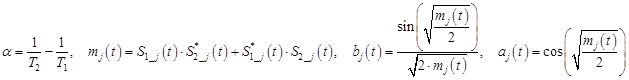 ;
;
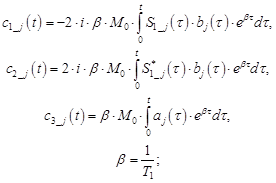
![]() – неоднородно уширенная линия, которую считаем постоянной в пределах ширины спектров радиочастотных импульсов,
– неоднородно уширенная линия, которую считаем постоянной в пределах ширины спектров радиочастотных импульсов, ![]() – начальная намагниченность, T1 – время продольной (спин-решеточной) релаксации, T2 – время поперечной (спин-спиновой) релаксации.
– начальная намагниченность, T1 – время продольной (спин-решеточной) релаксации, T2 – время поперечной (спин-спиновой) релаксации.
Изучено влияние помех на корреляционную обработку сигналов, в случае, если первый сигнал является радиоимпульсом с линейной частотной модуляцией (ЛЧМ), второй представляет собой смесь ЛЧМ-сигнала и шума, а третий – очень короткий типа дельта-функции. Ввиду сложности выражения (1) нахождение эхо-сигнала было проведено путем численного интегрирования. На рис. 1 показана зависимость отношения сигнал-шум на выходе![]() от отношения сигнал-шум на входе
от отношения сигнал-шум на входе![]() , оба отношения отложены в дБ. Видно, что при небольших мощностях шума зависимость практически линейная, а с ростом мощности шума, что соответствует уменьшению отношения сигнал-шум, появляется нелинейность, что легко понять из формулы (1), так как при больших шумах сказываются входящие в нее нелинейные члены.
, оба отношения отложены в дБ. Видно, что при небольших мощностях шума зависимость практически линейная, а с ростом мощности шума, что соответствует уменьшению отношения сигнал-шум, появляется нелинейность, что легко понять из формулы (1), так как при больших шумах сказываются входящие в нее нелинейные члены.
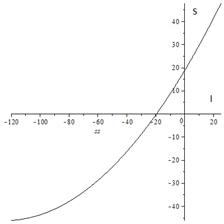
Рисунок 1. Зависимость отношения сигнал-шум на выходе от отношения сигнал-шум на входе. Длительность шумового сигнала в 5 раз больше, чем длительность ЛЧМ
Далее рассмотрим особенности сигналов спинового эха в ферромагнитных поликристаллах. В [1,9] рассматривалось возбуждение спинового эха случайными сигналами типа белого шума. Здесь рассмотрено импульсное возбуждение спинового эха в поликристаллическом образце, в каждом микрокристалле которого существует внутреннее постоянное магнитное поле, направленное случайным образом. Исследован случай, когда ядра имеют спин ½. При воздействии на образец двух радиочастотных импульсов наблюдается спиновое эхо. В качестве первого импульса используется произвольный радиочастотный импульс, а второго – очень короткий импульс типа дельта-функции площадью ![]() .
.
Известно, что в ферромагнетиках величина радиочастотного поля, действующего на ядра, усилена за счет сверхтонкого взаимодействия ядер с электронами в ![]() раз, где
раз, где ![]() – неоднородный коэффициент усиления [8].
– неоднородный коэффициент усиления [8]. ![]() значительно больше для ядер, находящихся в стенках, разделяющих соседние домены, чем в центральных областях доменов. Поэтому основной вклад в эхо-сигнал дают ядра в стенках. Будем считать
значительно больше для ядер, находящихся в стенках, разделяющих соседние домены, чем в центральных областях доменов. Поэтому основной вклад в эхо-сигнал дают ядра в стенках. Будем считать ![]() константой, и под величиной радиочастотного поля подразумевать уже усиленную в
константой, и под величиной радиочастотного поля подразумевать уже усиленную в ![]() раз напряженность поля.
раз напряженность поля.
В предположении, что все направления внутреннего постоянного поля равновероятны и для возникающего при вычислениях мультипликативного интеграла достаточно ограничиться нулевым приближением, путем усреднения по сферическим углам ![]() найдена намагниченность для сигнала двухимпульсного эха во всем поликристаллическом образце
найдена намагниченность для сигнала двухимпульсного эха во всем поликристаллическом образце
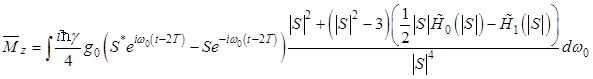 ,(2)
,(2)
где ![]() – спектр радиоимпульса, частота заполнения
– спектр радиоимпульса, частота заполнения ![]() которого близка к центральной частоте
которого близка к центральной частоте ![]() , и длительность
, и длительность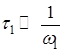 ,
, ![]() – специальные функции Струве,
– специальные функции Струве, ![]() – постоянная в пределах ширины спектра
– постоянная в пределах ширины спектра ![]() неоднородно уширенная линия.
неоднородно уширенная линия.
Вместо уравнения Шредингера для волновой функции системы можно использовать уравнения Блоха непосредственно для намагниченности. Был проведен расчет без учета релаксации, и полученное выражение для намагниченности полностью аналогично (2).
На рис. 2 показана зависимость амплитуды спинового эха от площади импульса радиочастотного поля ![]() , рассчитанная для радиочастотного импульса с прямоугольной огибающей с амплитудой напряженности
, рассчитанная для радиочастотного импульса с прямоугольной огибающей с амплитудой напряженности ![]() ,
, ![]() и длительностью
и длительностью ![]() . Величина амплитуды эхо-сигнала отложена в относительных единицах.
. Величина амплитуды эхо-сигнала отложена в относительных единицах.
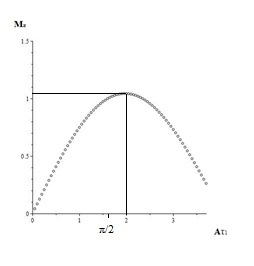
Рисунок 2. Зависимость амплитуды эхо-сигнала от площади радиочастотного импульса.
Так как при вычислении мультипликативного интеграла было использовано нулевое приближение, то полученные результаты справедливы при площади радиочастотного сигнала не более чем ![]() . При больших площадях радиочастотного сигнала для расчета величины эха необходимо использовать следующие приближения для мультипликативного интеграла. При этом появятся спектры сигнала на частоте, сдвинутой по отношению к частоте
. При больших площадях радиочастотного сигнала для расчета величины эха необходимо использовать следующие приближения для мультипликативного интеграла. При этом появятся спектры сигнала на частоте, сдвинутой по отношению к частоте ![]() . Величина сдвига будет зависеть от величины радиочастотного сигнала [7].
. Величина сдвига будет зависеть от величины радиочастотного сигнала [7].
Также в работе были рассмотрены особенности ЯКР при двухчастотном возбуждении по сравнению с одночастотным. При импульсном возбуждении образец подвергается воздействию радиочастотных импульсов (импульсы с высокочастотным заполнением). Сигналы ЯКР при этом наблюдаются после импульсов. В работе [5] были предприняты попытки рассчитать сигналы эха для радиочастотных импульсов конкретной формы, а впоследствии авторы занимались исследованием конкретных веществ. В данной работе рассматривается воздействие радиочастотных импульсов совершенно произвольной формы.
При воздействии двух импульсов на одинаковой частоте сигнал двухимпульсного эха
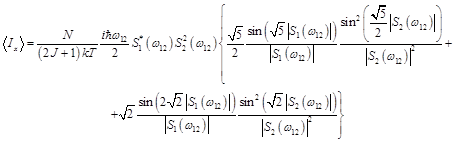 , (3)
, (3)
где ![]() – число частиц в системе, T – ее температура,
– число частиц в системе, T – ее температура,![]() – собственная частота перехода,
– собственная частота перехода, ![]() – собственные значения невозмущенного гамильтониана системы,
– собственные значения невозмущенного гамильтониана системы,![]() – спектры первого и второго сигналов.
– спектры первого и второго сигналов.
При воздействии первого импульса на двух частотах
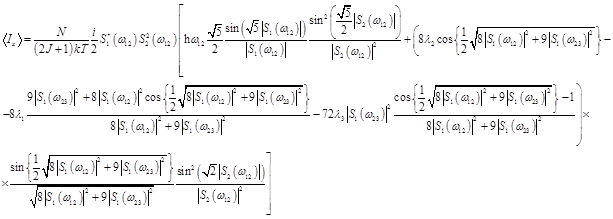 , (4)
, (4)
где ![]() .
.
При двухчастотном воздействии достигается усиление эхо-сигнала по сравнению с одночастотным
![]() . (5)
. (5)
В этой работе также установлены условия, при которых может быть выполнен анализ спектров сигналов в спиновых эхо-процессорах в реальном масштабе времени.
Явление спинового эха используется для создания управляемых линий задержек и других устройств обработки сигналов. Спиновые эхо-процессоры (СЭП), принцип действия которых основан на явлениях спинового или светового эха, отличаются простотой изготовления и настройки, относительно малыми габаритами. Было показано [6], что в СЭП возможно осуществить получение спектров сигналов в реальном масштабе времени трехимпульсным методом, используя в качестве третьего управляющего импульса сигнал с линейной частотной модуляцией (ЛЧМ), при выполнении условия
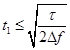 , (6)
, (6)
где t1 – длительность анализируемого сигнала, τ – длительность ЛЧМ, 2Δf – величина девиации частоты ЛЧМ импульса. Также при этом необходимо использование фазового детектора.
Целесообразно установить возможность получения в спиновых эхо-процессорах спектров сигналов в реальном масштабе времени по трехимпульсной методике без применения дополнительных устройств.
Показано, что для этого спектр третьего управляющего импульса S3(ω) должен быть равен
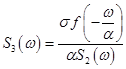 , (7)
, (7)
где ![]() – константа, имеющая размерность [с-2],
– константа, имеющая размерность [с-2], ![]() – константа, имеющая размерность [с-1],
– константа, имеющая размерность [с-1], ![]() – исследуемый сигнал (
– исследуемый сигнал (![]() – гиромагнитное отношение,
– гиромагнитное отношение, ![]() – напряженность радиочастотного поля), S2(ω) – спектр исследуемого сигнала.
– напряженность радиочастотного поля), S2(ω) – спектр исследуемого сигнала.
Из (7) видно, что для спектрального анализа сигнала в реальном времени управляющий сигнал должен определенным образом зависеть от свойств исследуемого сигнала.
Интересен вопрос, каким должен быть спектр исследуемого сигнала, чтобы при использовании в качестве управляющего импульса сигнала ЛЧМ на выходе СЭП получался этот спектр в реальном масштабе времени.
Выяснено, что спектр исследуемого сигнала![]() должен удовлетворять однородному уравнению Фредгольма 2-го рода
должен удовлетворять однородному уравнению Фредгольма 2-го рода
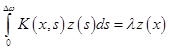 , (8)
, (8)
с ядром
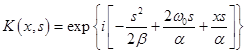 , (9)
, (9)
где ![]() ,
, ![]() – константа, имеющая размерность с-1,
– константа, имеющая размерность с-1,![]() ,
, ![]() – начальная частота ЛЧМ импульса,
– начальная частота ЛЧМ импульса,![]() – ширина спектра ЛЧМ импульса, β – скорость изменения частоты в импульсе. Уравнение (8) имеет счетное множество линейно независимых решений.
– ширина спектра ЛЧМ импульса, β – скорость изменения частоты в импульсе. Уравнение (8) имеет счетное множество линейно независимых решений.
Например, для ЛЧМ с параметрами![]() ,
, ![]() ,
,![]() на рис. 3 показаны модуль и фаза одного из решений.
на рис. 3 показаны модуль и фаза одного из решений.
 a
a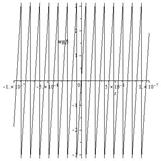 b
b
Рисунок 3. Модуль (a) и фаза (b) исследуемого сигнала
Таким образом, установлено, что только для исследуемых радиоимпульсов, принадлежащих определенному счетному множеству, при использовании в качестве управляющего импульса сигнала ЛЧМ на выходе СЭП можно получить спектр исследуемого импульса в реальном масштабе времени.
Заключение
Найдена зависимость амплитуды эхо-сигнала от площади радиочастотного импульса при двухимпульсном возбуждении в ферромагнитных поликристаллах.
Исследованный эффект усиления эхо-сигнала при двухчастотном воздействии по сравнению с одночастотным воздействием дает возможность разработки более чувствительных эхо-спектрометров и усовершенствования эхо-процессоров.
Найдено условие для получения в спиновых эхо-процессорах спектров сигналов в реальном масштабе времени по трехимпульсной методике без применения дополнительных устройств.
Рецензенты:
Бичурин М.И., д.ф.-м.н., профессор, заведующий кафедрой ПТРА, ГОУ ВПО «Новгородский государственный университет им. Ярослава Мудрого», г. Великий Новгород.
Рассветалов Л.А., д.т.н., профессор, профессор кафедры радиосистем ИЭИС, ГОУ ВПО «Новгородский государственный университет им. Ярослава Мудрого», г. Великий Новгород.



