Введение. Для описания вероятностных характеристик движения автомобиля типа v (имеющего при свободном движении скорость в пределах v, v+Δv) достаточно знать Р(v) – вероятность свободного движения этого автомобиля.
Моделирование движения автомобиля процессом Маркова позволяет составить дифференциальные уравнения, решение которых дает искомую вероятность при различных режимах движения потока.
Методика. Поток автомобилей поделим на достаточно большое число скоростных групп с интервалом скорости Δv. Выберем конкретный автомобиль, который принадлежит к j-ой скоростной группе и имеет скорость в пределах vj, vj+Δv. В некоторой точке х дороги вследствие ограничения обгонов встречным потоком, автомобиль типа vj может иметь скорость в пределах vj, vj+ Δv.
В соответствии с терминологией процессов Маркова можно сказать, что автомобиль типа j в точке х находится в состоянии k=1, 2, 3, ..... j, то есть в точке х автомобиль типа j имеет скорость в пределах vк, vк+ Δv.
Введем состояние m, которое обозначает ситуацию обгона. Возможные переходы из состояния в состояние представлены на рисунке 1.
Вероятность перехода Рi,r на участке от х до х+Δх из состояния i в состояние r согласно теории Маркова определяется уравнением:
Pi,r = Mi,rΔx, (1)
где Mi,r - плотность перехода из состояния i в состояние r.
Плотности переходов зависят от условий движения автомобиля в потоке. Величина, обратная плотности перехода, - это средний путь, который проходит автомобиль, ожидая перехода из состояния i в состояние r.
В случайных процессах плотности Mi,r - это параметр потока случайных событий, переводящих автомобиль из состояния i в состояние r. В Марковских процессах Mi,r - параметр простейшего потока, обладающего свойствами стационарности, отсутствия последствия и ординарности.
Потоки случайных событий, переводящих автомобиль из состояния в состояние, в достаточной степени обладает указанными свойствами, и предлагаемое ожидание процесса движения автомобиля в транспортном потоке достаточно близко к Марковскому процессу [1-5].
Свойство стационарности предполагает неизменность интенсивности потока и достаточную длину участка дороги с постоянными дорожными условиями. В этом случае количество событий определенного потока не зависит от месторасположения автомобиля на участке дороги. Практически все исследователи транспортных потоков явно или неявно считали их стационарным на некоторых участках дороги и в некоторые ограниченные периоды времени. Можно считать, опираясь на этот опыт, что потоки стационарны в часовые интервалы времени на участках дороги с примерно постоянными дорожными условиями (количество полос, состояние покрытия, продольный уклон и др.) [3,4,7].
В предложенном описании процесса движения автомобиля в потоке плотности Mi,r потоков, переводящих автомобиль типа j из состояния i в состояние r, очень малы. Плотности Mi,r определяются количеством автомобилей типа r, которое равно λƒ(vr)Δv (здесь λ - плотность всего потока автомобилей). Так как Δv достаточно малая величина, то плотности Mi,r невелики.
Автомобили типа r, которые последовательно догоняют исследуемый автомобиль типа j, расположены на дороге очень далеко друг от друга и поэтому взаимно независимы. Автомобиль типа j догоняет автомобиль типа r в последовательные моменты времени, независящие друг от друга.
Такое описание процесса движения автомобиля в потоке позволяет считать, что в предложенной модели процесса последствие отсутствует.
Поскольку водитель автомобиля типа j взаимодействует в последовательные моменты времени только с одним автомобилем типа r, то поток событий, переводящий автомобиль типа j в состояние r, обладает свойством ординарности.
Таким образом, потоки событий, показанные на графе переходов, достаточно близки к простейшим пуассоновским потокам, а предложенная вероятностная модель может быть описана марковским случайным процессом [1,6,9].
В состоянии 1, 2, 3, ......... j-1 автомобиль типа j переходит из состояния j при невозможности начать обгон "с ходу" в пределах х, х+Δх. Обозначенная возможность обгона "с ходу" для автомобиля типа j через η, можно записать для автомобиля типа j вероятность перехода в состояние k = 1, 2, 3, ..., j-1 на участке от х до х+Δх в виде:
Pj,k = (1-η)Мik , (2)
где Мik - вероятность перехода из состояния j в состояние k на участке от х до х+Δх при невозможности обгона.
Вероятность Мik есть вероятность того, что автомобиль типа j (который находится в точке х и имеет скорость в пределах vj, vj+Δv) догонит автомобиль типа k до точки х+Δх.
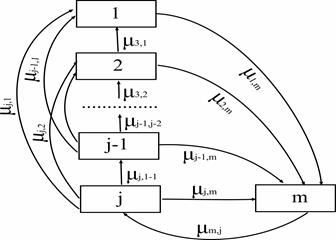
Рисунок 1. Переходы автомобиля типа j в состояние 1,2….j-1, m
Для расчета вероятностей Мik сначала найдем координату точки аi,k, которая имеет следующую особенность. Если автомобиль типа k находится в интервале х, аi,k, то автомобиль типа j (который находится в точке х) всегда догонит автомобиль типа k до точки х+Δх. Координата точки аi,k находится из равенства времени движения: 1) автомобиля типа j (имеющего скорость в пределах vj, vj+Δv) от х до х+Δх; 2) автомобиля типа k (имеющего скорость в пределах vk, vk+Δv) от аi,k до х+Δх, т.е.
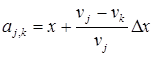. (3)
Вероятность Мik равна отношению интервала х, аi,k к средней величине свободного расстояния 1/λ΄k между автомобилями типа k .
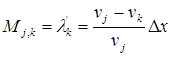, (4)
подставляя (4) в (2), имеем
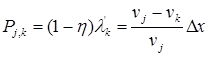. (5)
Из состояния j в состояние m автомобиль типа j переходит в пределах х, х+Δх при возможности начать обгон «с ходу», вероятность этого перехода равна
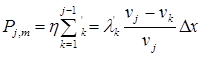, (6)
где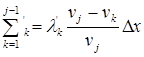 
– вероятность того, что автомобиль типа j догонит в пределах х; х+Δх или автомобиль типа 1 или типа 2… или типа j-1, т.е. любой автомобиль, скорость которого меньше vj.
Из состояния 1, 2, 3, …, k, …, j-1 автомобиль типа j переходит в состояние m в пределах х, х+Δх для выполнения обгона после ожидания благоприятных условий для обгона [5,8,10].
Различия обгонов «с ходу» и «с ожиданием» представлены на рисунке 2. Обгон «с ходу» возникает, когда автомобиль типа j догнал автомобиль типа k, vj>vk и во встречном потоке имеется интервал, достаточный для обгона. При этом начало обгона не совпадает с моментом проезда встречного автомобиля мимо обгоняющего. Таким образом
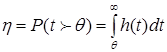, (7)
где h(t) – плотность вероятностей интервала между автомобилями; θ – интервал достаточный для обгона.
Вероятность возможности обгона «с ожиданием» вычисляется следующим образом. Так как автомобиль типа j находится в ожидании обгона, то этому (ожиданию обгона) способствуют следующие события, относящиеся к потоку встречного движения: а) на участке х, х+Δх находится какой-нибудь автомобиль встречного потока на своей полосе, либо б) 1) на участке х, х+Δх нет автомобилей встречного потока на своей полосе, 2) за точкой х+Δх во встречном потоке нет интервала, большего чем θ.
Рисунок 2. Схема к расчету вероятности обгона. Треугольники – автомобили встречного потока; 1 – начало обгона «с ходу», 2 – начало обгона «с ожиданием».
Таким образом, возможность обгона после его ожидания и следования за тихоходным автомобилем имеет место, если возникают следующие события: а) на участке х, х+Δх находится какой-нибудь автомобиль встречного потока, вероятность его равна λ'λΔх; б) после точки х, х+Δх во встречном потоке есть интервал, достаточный для обгона, вероятность его равна ηj.
Таким образом, для любого из состояний 1, 2, 3, ...k,.... j-1 вероятность перехода автомобиля типа j в состояние m из состояния k в пределах х, х+Δх:
. (8)
Из состояния m автомобиль типа j возвращается в состояние j после окончания обгона на участке х, х+Δх. Вероятность окончания обгона на участке х, х+Δх равна отношению Δх к длине пути обгона Sj. Принимаем среднюю скорость за время обгона равной скорости свободного движения, тогда вероятность перехода автомобиля типа j из состояния m в состояние j равна
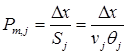. (9)
Коэффициенты при Δх есть плотности соответствующих переходов. Согласно этим плотностям можно разметить граф переходов на рисунке 1 и составить систему дифференциальных уравнений.
В левой части уравнения поставим производную P´k, в правой – столько членов, сколько стрелок связано с состоянием k (если стрелка ведет в левое состояние, член имеет знак плюс и наоборот). Каждый член равен плотности переходов, перемноженной на вероятность того состояния, из которого идет левая стрелка. Для решения нашей задачи достаточно составить уравнение для состояний j и m:
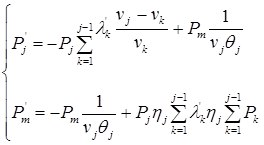. (10)
Для практических расчетов при непрерывном распределении скорости преобразуем систему (10) следующим образом. В качестве конкретного автомобиля выбираем такой автомобиль, скорость свободного движения которого попадает в интервал v, v+Δv. Такой автомобиль будем называть автомобилем типа v, что соответствует типу j. Аналогично P(v) и ƒ(v) соответствует Pj и Pm.
Тогда в системе (10) можно перейти от суммы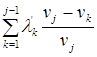 
к интервалу, принимая
λ'k=Λ'nƒ(vk)Δv, (11)
где ƒ(v) – плотность вероятностей скорости свободного движения; Λ'n – средняя величина свободного расстояния между автомобилями при плотности Λn.
С учетом преобразований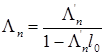 
, (12), где l0 – средняя величина динамического габарита при плотности потока Λn. Поэтому 
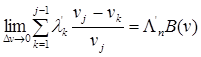, (13), где 
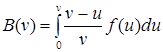. (14)
Второе преобразование заключается в замене в последнем уравнении системы (8) суммы 
на 1-Pm-Pj.
Тогда, опуская индексы и переходя к непрерывному распределению скорости
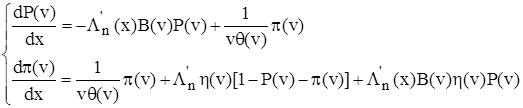, (15)
Таким образом, применение процессов Маркова для моделирования потока существенно упрощает методику составления дифференциальных уравнений, описывающих вероятностные характеристики движения отдельного автомобиля в потоке. При различных дорожных условиях изменяются начальные условия системы (15) и тем самым определяются различные режимы движения автомобильных потоков. Классификация решений системы (15) в зависимости от дорожных условий на двухполосных дорогах.
Принципы моделирования движения автомобилей в потоке, разработанные в предыдущих разделах, могут быть применены при моделировании движения потоков по многополосным дорогам.
Вывод. Автором разработан общий метод моделирования движения автомобильного потока, основанный на использовании процессов Маркова, отличающийся от известных методов и моделей потока следующим: основные положения метода применимы к моделированию движения по дорогам с различным количеством полос движения; количество скоростных групп, характеристики движения которых исследуются, не ограничено; практически не ограничен диапазон вариации дорожных условий, определяющих режимы движения потоков; результатами моделирования служат не только средние характеристики потока, но также характеристики движения в потоке отдельных автомобилей и отдельных типовых групп потока, что в дальнейшем использовано для повышения достоверности и точности показателей движения автомобилей; исходной информацией для моделирования движения автомобилей в потоке служат результаты моделирования свободного движения. Такой комплексный подход позволяет учитывать динамику тягово-скоростных свойств автомобилей, расширяет состав потока; с существенной полнотой отражаются в транспортно-эксплуатационных характеристиках параметры плана продольного и поперечного профилей, тип и количество дорожной одежды, дорожная обстановка.
Применением метода процессов Маркова достигнут переход от малого числа скоростных групп (2, 3 группы) к непрерывному распределению скорости. Тем самым достигнута большая общность при формировании основных положений модели. Предложены практические модели исследования движения автомобилей в потоке на однополосных дорогах и двухполосных дорогах (дороги II – IV категорий).
Рецензенты:
Яковлев К.А., д.т.н., доцент кафедры производства, ремонта и эксплуатации машин ФГБОУ ВПО «Воронежская государственная лесотехническая академия», г. Воронеж.
Кондрашова Е.В., д.т.н., профессор кафедры технического сервиса и технологии машиностроения ФГБОУ ВПО «Воронежский государственный аграрный университет имени императора Петра I», г. Воронеж.