Введение
Теория идентификации занимается построением математических моделей объектов управления по опытным данным, полученным в результате эксперимента или нормальной работы [6]. Успешность решения задачи идентификации объекта управления во многом зависит от качества используемых при этом данных измерений «входных-выходных» переменных процесса. По различным причинам данные могут содержать в себе пропуски (неисправность измерительного прибора, ошибка в работе оператора, сложность контроля измеряемых переменных и др.). Пропуски в наблюдениях «входных-выходных» переменных процесса значительно усложняют процесс построения математической модели. Кроме того, задача усложняется работой в условиях неполной информации, наличием многих случайных факторов.
Проблеме обработки данных с пропусками посвящено много работ, в частности различные методы представлены в книге Р.Дж. Литтла и Д.Б. Рубина [2]. Представленные в работе методы в своем большинстве относятся к классу параметрических. Параметрические методы предполагают наличие значительного объема априорных сведений об объекте исследования, в том числе и знания о его структуре [5]. Но на практике мы не всегда обладаем этими сведениями. В этих случаях поиск подходящей параметрической структуры требует существенных усилий.
В работе предлагается использовать метод заполнения пропусков «входных-выходных» переменных процесса, основанный на непараметрических алгоритмах. Отличие непараметрических методов от общепринятых параметрических состоит в отсутствие этапа выбора параметризованной структуры модели на основании имеющейся априорной информации [3]. В этом случае требования к априорной информации ослабевают. Здесь требуется информация на качественном уровне (статический или динамический объект, линейный или нелинейный и др.). Непараметрические методы в значительной степени базируются на непараметрической оценке функции регрессии по наблюдениям, которая и используется в работе.
Постановка задачи
Рассмотрим достаточно общую схему исследуемого процесса, принятую в теории идентификации (рис. 1).
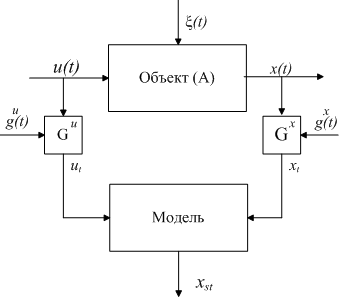
Рисунок 1. Общая схема идентификации исследуемого процесса.
Здесь приняты следующие обозначения: А – неизвестный оператор объекта; ![]() – входное воздействие;
– входное воздействие; ![]() – выходная переменная; (t) – непрерывное время;
– выходная переменная; (t) – непрерывное время; ![]() – случайное воздействие, действующее на процесс;
– случайное воздействие, действующее на процесс; ![]() ,
, ![]() – измерения
– измерения ![]() ,
, ![]() через дискретные моменты времени
через дискретные моменты времени ![]() ;
; ![]() ,
, ![]() – блоки контроля переменных;
– блоки контроля переменных; ![]() ,
, ![]() – случайные помехи измерений, действующие в блоках контроля, имеют нулевое математическое ожидание и ограниченную дисперсию. Измерения «входных-выходных» переменных процесса поступают на блок «Модель», в который «включена» соответствующая модель процесса,
– случайные помехи измерений, действующие в блоках контроля, имеют нулевое математическое ожидание и ограниченную дисперсию. Измерения «входных-выходных» переменных процесса поступают на блок «Модель», в который «включена» соответствующая модель процесса, ![]() – выход блока «Модель». Исследуемый процесс может быть представлен в виде:
– выход блока «Модель». Исследуемый процесс может быть представлен в виде:
![]() , (1)
, (1)
где ![]() – запаздывание по различным каналам процесса. Не следует путать запаздывание
– запаздывание по различным каналам процесса. Не следует путать запаздывание ![]() , присущее процессу, и задержку при измерении тех или иных переменных процесса.
, присущее процессу, и задержку при измерении тех или иных переменных процесса.
Рассматриваемый процесс относится к классу дискретно-непрерывных, т.е. процесс является непрерывным, но его «входные-выходные» переменные контролируются с помощью дискретных средств контроля.
Пусть контроль входной переменной ![]() (рис. 1) может осуществляться через незначительные промежутки времени
(рис. 1) может осуществляться через незначительные промежутки времени ![]() . Для измерения выходной переменной
. Для измерения выходной переменной ![]() требуется большее время
требуется большее время ![]() . При этом
. При этом ![]() . В результате переменные процесса контролируются с различной дискретностью, что приводит к появлению в данных пропусков. Матрица наблюдений «входных-выходных» переменных процесса в этом случае имеет следующий вид (табл. 1).
. В результате переменные процесса контролируются с различной дискретностью, что приводит к появлению в данных пропусков. Матрица наблюдений «входных-выходных» переменных процесса в этом случае имеет следующий вид (табл. 1).
Таблица 1 - Матрица наблюдений «входных-выходных» переменных с пропусками
|
u |
x |
|||
|
u1 |
u2 |
... |
um |
|
|
u11 |
u21 |
... |
um1 |
x1 |
|
u12 |
u22 |
... |
um2 |
12-'> |
|
u13 |
u23 |
... |
um3 |
12-'> |
|
u14 |
u24 |
... |
um4 |
x4 |
|
... |
... |
... |
... |
... |
|
u1s |
u2s |
... |
ums |
xs |
В таблице 1 столбцы представляют собой переменные процесса, а строки – наблюдения. Принято, что дискретность измерения выходной переменной ![]() в три раза больше дискретности измерения входной переменной
в три раза больше дискретности измерения входной переменной ![]() (
(![]() ), s – объем исходной выборки.
), s – объем исходной выборки.
Пропуски в данных значительно усложняют процесс моделирования и снижают точность решения задачи идентификации. В связи с этим интерес представляет задача заполнения пропусков «входных-выходных» переменных процесса с целью повышения качества моделирования.
При решении задачи идентификации можно использовать только полностью заполненные строки матрицы наблюдений, не учитывая строки с пропусками, но при этом теряется важная информация о процессе, что является нецелесообразным. Кроме того, для решения задачи идентификации предпочтительно иметь выборки большего объема. Следовательно, заполнение пропусков переменных матриц наблюдений является важной задачей. Для решения этой задачи, как было отмечено ранее, можно воспользоваться методами параметрической [5] и непараметрической идентификации [3].
Параметрическая и непараметрическая идентификация
Параметрическая идентификация (идентификация в «узком» смысле) состоит из двух этапов: идентификация параметрической структуры модели и идентификация параметров в модели выбранной структуры [5]. Данный класс идентификации требует высокого уровня априорной информации об исследуемом объекте. Но зачастую имеющихся априорных сведений не достаточно для выбора параметризованной структуры модели исследуемого объекта, однако мы можем иметь информацию о его качественных свойствах. В этих случаях целесообразно воспользоваться методами идентификации в «широком» смысле (методами непараметрической идентификации).
О процессе идентификации в «широком» смысле пишет Н.С. Райбман в предисловии к книге П. Эйкхоффа [6]. Эти методы более универсальны, так как используют только исходную статистическую выборку «входных-выходных» переменных исследуемого процесса и некоторые описательные характеристики объекта (статистический или динамический объект, линейный или нелинейный и др.). К таким методам относится непараметрическая оценка функции регрессии по наблюдениям.
Методика заполнения матрицы наблюдений
Для заполнения пропусков в матрицах наблюдений предлагается дать оценки ![]() выходной переменной
выходной переменной ![]() в незаполненных строках матрицы наблюдений (табл. 1) при известных значениях входных переменных
в незаполненных строках матрицы наблюдений (табл. 1) при известных значениях входных переменных ![]() . Для восстановления пропусков используется выборка, состоящая только из результатов заполненных строк матрицы наблюдений. В итоге мы получим заполненную матрицу, представленную в таблице 2, и оценки
. Для восстановления пропусков используется выборка, состоящая только из результатов заполненных строк матрицы наблюдений. В итоге мы получим заполненную матрицу, представленную в таблице 2, и оценки ![]() будем осуществлять уже на основании заполненной матрицы наблюдений.
будем осуществлять уже на основании заполненной матрицы наблюдений.
Таблица 2 – Заполненная матрица наблюдений
|
u |
x |
|||
|
u1 |
u2 |
... |
um |
|
|
u11 |
u21 |
... |
um1 |
x1 |
|
u12 |
u22 |
... |
um2 |
xs2 |
|
u13 |
u23 |
... |
um3 |
xs3 |
|
u14 |
u24 |
... |
um4 |
x4 |
|
... |
... |
... |
... |
... |
|
u1s |
u2s |
... |
ums |
xs |
В качестве приближения ![]() можно использовать условное математическое ожидание
можно использовать условное математическое ожидание ![]() . Для его оценки можно использовать как параметрические оценки функции регрессии [5], так и непараметрические [3; 4]. Предложенный прием, как это будет показано ниже, оказывается вполне оправданным, так как задача идентификации в последнем случае (табл. 2) решается более точно, чем в случае, когда мы исключаем строки с пропусками из матрицы наблюдений.
. Для его оценки можно использовать как параметрические оценки функции регрессии [5], так и непараметрические [3; 4]. Предложенный прием, как это будет показано ниже, оказывается вполне оправданным, так как задача идентификации в последнем случае (табл. 2) решается более точно, чем в случае, когда мы исключаем строки с пропусками из матрицы наблюдений.
Непараметрическая оценка функции регрессии по наблюдениям
Пусть даны наблюдения ![]() случайных величин
случайных величин ![]() ,
, ![]() , распределенных с неизвестными плотностями вероятности
, распределенных с неизвестными плотностями вероятности ![]() , причем
, причем ![]() . Для восстановления
. Для восстановления ![]() используются непараметрические оценки вида:
используются непараметрические оценки вида:
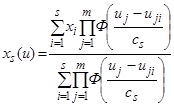 , (2)
, (2)
где 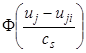 – ядерная функция и коэффициент размытости ядра
– ядерная функция и коэффициент размытости ядра ![]() удовлетворяют некоторым условиям сходимости [4]. Параметр размытости
удовлетворяют некоторым условиям сходимости [4]. Параметр размытости ![]() определяется в соответствии со следующим критерием:
определяется в соответствии со следующим критерием:
![]() (3)
(3)
где ![]() – временные векторы. Оценка качества полученных моделей
– временные векторы. Оценка качества полученных моделей ![]() производится в соответствии со следующей формулой:
производится в соответствии со следующей формулой:
![]() , (4)
, (4)
где ![]() – относительная ошибка моделирования,
– относительная ошибка моделирования, ![]() – оценка математического ожидания выходной переменной
– оценка математического ожидания выходной переменной ![]() :
: ![]() .
.
Этапы восстановления пропусков матрицы наблюдений
Рассмотрим основные этапы восстановления пропусков матрицы наблюдений на примере восстановления выходной переменной ![]() [1].
[1].
На первом этапе восстанавливается функция регрессии ![]() (2) по наблюдениям
(2) по наблюдениям ![]() по выборке объема
по выборке объема ![]() , полностью представленным в исходной матрице измерений, то есть по полностью заполненным строкам в результате эксперимента (в таблице 1 – это первая, четвертая, седьмая и т.д. строки). Строки с пропусками значений выхода
, полностью представленным в исходной матрице измерений, то есть по полностью заполненным строкам в результате эксперимента (в таблице 1 – это первая, четвертая, седьмая и т.д. строки). Строки с пропусками значений выхода ![]() на данном этапе не учитываются (объем выборки в этом случае равен
на данном этапе не учитываются (объем выборки в этом случае равен ![]() ). Находится оптимальное значение коэффициента
). Находится оптимальное значение коэффициента ![]() (3).
(3).
Затем происходит заполнение пропусков в матрице наблюдений c использованием оценки ![]() , полученной на предыдущем этапе. Там, где наблюдения
, полученной на предыдущем этапе. Там, где наблюдения ![]() пропущены, в оценку
пропущены, в оценку ![]() подставляем значения измеренных
подставляем значения измеренных ![]() и вычисляем соответствующую оценку
и вычисляем соответствующую оценку ![]() , которой восполняем недостающее наблюдение
, которой восполняем недостающее наблюдение ![]() (например, недостающая
(например, недостающая ![]() в представленной таблице 2 заполнена значением
в представленной таблице 2 заполнена значением ![]() ).
).
На заключительном этапе осуществляется построение непараметрической оценки ![]() по заполненной матрице наблюдений объема
по заполненной матрице наблюдений объема ![]() . Отметим, что в случае использования непараметрических методов для восстановления пропусков «входных-выходных» переменных процесса нам необходимо иметь выборку наблюдений вида
. Отметим, что в случае использования непараметрических методов для восстановления пропусков «входных-выходных» переменных процесса нам необходимо иметь выборку наблюдений вида ![]() и обладать сведениями о качественном характере процесса.
и обладать сведениями о качественном характере процесса.
Вычислительный эксперимент
Для вычислительного эксперимента примем объект, на вход которого подается входная переменная ![]()
![]() , на выходе объекта - скаляр
, на выходе объекта - скаляр ![]() . Матрица наблюдений «входных-выходных» переменных объекта имеет вид, представленный в таблице 1, то есть дискретность контроля
. Матрица наблюдений «входных-выходных» переменных объекта имеет вид, представленный в таблице 1, то есть дискретность контроля ![]() выходной переменной
выходной переменной ![]() в три раза больше дискретности контроля
в три раза больше дискретности контроля ![]() входной переменной
входной переменной ![]() (
(![]() ). Выходная переменная процесса
). Выходная переменная процесса ![]() описывается зависимостью:
описывается зависимостью:
![]() , (5)
, (5)
а переменная ![]() генерируется случайным образом по равномерному закону распределения. Зависимость (5) необходима для получения в компьютерном эксперименте соответствующих исходных выборок
генерируется случайным образом по равномерному закону распределения. Зависимость (5) необходима для получения в компьютерном эксперименте соответствующих исходных выборок ![]() . В дальнейшем характер данной зависимости предполагается неизвестным.
. В дальнейшем характер данной зависимости предполагается неизвестным.
Рассмотрим рисунок 2, на котором показаны графики зависимости относительной ошибки моделирования ![]() (4) (ось ординат) от объема исходной выборки
(4) (ось ординат) от объема исходной выборки ![]() (ось абсцисс) для трех матриц (истинной, с пропусками (табл. 1) и восстановленной (табл. 2)). Работать с истинной матрицей наблюдений мы можем лишь в рамках вычислительного эксперимента. Поскольку мы имеем дело со случайными величинами, то проводилось усреднение по результатам десяти экспериментов.
(ось абсцисс) для трех матриц (истинной, с пропусками (табл. 1) и восстановленной (табл. 2)). Работать с истинной матрицей наблюдений мы можем лишь в рамках вычислительного эксперимента. Поскольку мы имеем дело со случайными величинами, то проводилось усреднение по результатам десяти экспериментов.
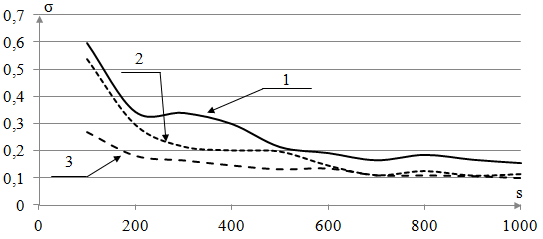
Рисунок 2. Результаты вычислительного эксперимента.
Для построения модели ![]() использовалась классическая непараметрическая оценка функции регрессии (2). Сначала оценка строилась по матрице наблюдений с пропусками по переменной
использовалась классическая непараметрическая оценка функции регрессии (2). Сначала оценка строилась по матрице наблюдений с пропусками по переменной ![]() , что соответствует реальности (график 1 на рис. 2, соответствующий наибольшей относительной ошибке моделирования σ). Затем по заполненной с помощью предложенной выше методике матрице (график 2). В заключение – по исходной матрице наблюдений без пропусков (график 3; такой возможностью мы обладаем только в рамках вычислительного эксперимента). Как видно из рисунка, оценка по заполненной матрице наблюдений близка к оценке по истинной матрице наблюдений. Из этого следует, что заполнение пропусков матрицы наблюдений позволяет повысить точность решения задачи идентификации.
, что соответствует реальности (график 1 на рис. 2, соответствующий наибольшей относительной ошибке моделирования σ). Затем по заполненной с помощью предложенной выше методике матрице (график 2). В заключение – по исходной матрице наблюдений без пропусков (график 3; такой возможностью мы обладаем только в рамках вычислительного эксперимента). Как видно из рисунка, оценка по заполненной матрице наблюдений близка к оценке по истинной матрице наблюдений. Из этого следует, что заполнение пропусков матрицы наблюдений позволяет повысить точность решения задачи идентификации.
Вычислительные эксперименты показали, что с увеличением количества пропусков эффект от восстановления снижается. Однако точность оценивания по восстановленной матрице наблюдений выше, чем по матрице с пропусками.
Заключение
В работе изложена задача анализа данных, связанная с наличием пропусков в матрице наблюдений. Пропуски в рассматриваемом случае связаны с различной дискретностью контроля «входных-выходных» переменных. Предложена непараметрическая методика восстановления матрицы наблюдений с пропусками. В этой связи рассмотрена задача восстановления матрицы наблюдений с пропусками для решения задачи идентификации статических объектов с запаздыванием. Показано, что заполнение пропусков приводит к повышению качества работы модели. Относительная ошибка моделирования после заполнения сокращается в среднем на 5-10%.
Рецензенты:
Демиденко Н.Д., д.т.н., профессор, СКТБ «Наука» КНЦ CO РАН, г. Красноярск.
Мурыгин А.В., д.т.н., профессор, зав. кафедрой информационно-управляющих систем ФГБОУ ВПО «Сибирский государственный аэрокосмический университет им. академика М.Ф. Решетнева», г. Красноярск.



