В настоящее время в школе недостаточно уделяется внимания построению изображений при решении геометрических задач. Из школьного курса обучения убрали черчение, учащихся никто не учит правильно изображать фигуры на плоскости и в пространстве. А для того чтобы решить геометрическую задачу, они должны представить и правильно изобразить конфигурацию, о которой идет речь. Геометрия относится к предметам математического цикла и имеет большое значение для изучения окружающего мира. В процессе решения геометрических задач создаются благоприятные условия для приобщения учащихся к творческой исследовательской деятельности и развитию их способностей. В связи с этим на уроках геометрии особое внимание должно уделяться умению работать с чертежом, моделируя условие задачи, в том числе формированию приемов работы с чертежом, так как они являются составляющей частью умения решать геометрические задачи.
Проблема приобщения учащихся к творческой деятельности и развития их способностей при решении геометрических задач через работу с чертежом решалась в двух направлениях.
Первое направление связано с возможностями применения эвристик при поиске решения геометрических задач, систематизации задач на основе основных геометрических конфигураций, активизации исследовательской деятельности учащихся при изучении геометрии. Это работы Н.Г. Воробьевой, Е.В. Ларькиной, С.А. Мищенко, Д. Пойа, Г.И. Саранцева, Н.Г. Шило др.
Второе направление основано на том, что геометрический чертеж выступает объектом исследования. В основном это психологические исследования, в которых большое внимание уделяется восприятию и пониманию чертежа в процессе решения задач. Вопросам чтения и переосмысления чертежа посвящены работы Е.Н. Кабановой-Меллер, И.С. Якиманской и др.
Проблеме обучения школьников умению работать с чертежом посвящены исследования А.К. Артемова, Г.А. Владимирского, А.Т. Зверевой, Д. Пойа, Г.И. Саранцева, Е.В. Силаева, А.В. Шатиловой и др. В них выделяются работы, относящиеся к обучению строить, читать и преобразовывать чертеж.
Особое внимание уделяется формированию умений «читать чертеж», так как это сложный процесс. Использование чертежа в процессе решения задачи предполагает умение «охватывать взором весь чертеж… и улавливать те соотношения между элементами чертежа, которые могут быть нужны при решении данного вопроса» (Д. Пойа), «умение мысленно преобразовывать фигуру» (Г.А. Владимирский). Выбор фигур, нужных для решения, определяется условием задачи. Но чтобы осуществить этот выбор необходимо хорошо ориентироваться в чертеже задачи.
Умения решать геометрическую задачу взаимосвязаны с умениями работы с чертежом, они основываются на единстве преобразований чертежа и преобразования задачной ситуации.
При работе с чертежом к геометрической задаче большое значение имеет специальное формирование соответствующих приемов. Прием – система действий, выполненных в определенной последовательности, служащих для решения учебных задач. Прием допускает обобщение, специализацию и конкретизацию. Он обладает свойством переносимости на другую задачу. Его можно перестроить и на его основе создать новый прием.
Приемы работы с чертежом могут быть разной степени сложности и обобщенности. Более сложный прием состоит из большого числа действий, включая в себя в качестве составляющих другие приемы.
Наиболее обобщенными являются приемы:
- Подведение геометрической фигуры под понятие, т.е. распознавание фигуры.
- Выделение геометрической фигуры на чертеже. Обнаружение фигуры осуществляется на основе ее зрительного образа, в котором должны быть отражены существенные признаки соответствующего понятия.
- Вывод непосредственных следствий.
- Установление вида геометрической фигуры на чертеже, если указан признак отличия, лежащий в основе классификаций фигур данного рода.
- Включение одного и того же элемента чертежа в разные конфигурации и выражение его в терминах этих фигур.
- Нахождение общих элементов геометрических фигур на чертеже.
- Разностороннее рассматривание геометрической фигуры на чертеже.
- Изменение взаимного расположения образов фигур, представленных на чертеже.
Обучение приемам работы с чертежом проводится совместно с решением задач на вычисление и доказательство. Каждый прием при необходимости может быть детализирован и представлен в виде отдельных действий.
Рассмотрим действия на основе приема выделения геометрической фигуры на чертеже:
1) актуализация существенных свойств понятия;
2) создание зрительного образа понятия;
3) обнаружение фигуры на чертеже;
4) вычленение фигуры из чертежа.
Обнаружение фигуры осуществляется на основе ее зрительного образа, в котором должны быть отражены существенные признаки понятия. На чертеже ученик не просто узнает фигуру по определению, а выделяет ее из множества других фигур. Прием имеет место и тогда, когда требуется выделить фигуру определенного вида, например, все треугольники, все равнобедренные трапеции.
Для обучения школьников приемам работы с чертежом применяются задачи трёх типов.
Обучение начинается с задач первого типа, в которых происходит анализ результатов деятельности по решению задачи (проверьте, объясните…). Задачи данного типа выступают средством введения и формирования приемов работы с чертежом, и чаще всего это упражнения на готовых чертежах.
Затем предлагаются задачи второго типа, в которых учащиеся действуют в аналогичной или новой ситуации (выпишите, примените, выполните…). Они являются средством обработки и применения приемов, не требующих преобразований.
И, наконец, рассматриваются задачи третьего типа. Это задачи исследовательского характера, в которых учащиеся должны сами найти решение с применением эвристических приемов. Умению решать задачи данного типа предшествует обучение решению задач первого и второго типа. Они отрабатывают умение применять приемы, преобразовывая чертеж в единстве с преобразованием задачной ситуации.
Как говорилось выше, одним из средств формирования приемов работы с геометрическим чертежом являются упражнения на готовых чертежах. Упражнения на готовых чертежах как средство активизации мышления учащихся делятся на две группы:
- готовые чертежи – иллюстрация условия геометрической задачи;
- задания на составление задач по готовым чертежам. В свою очередь такие задания делятся на:
I тип:
1) задача с определенным условием и требованием;
2) задача с определенным условием, но неопределенным требованием;
3) задача с неопределенным условием и определенным требованием;
4) задача с неопределенным условием и требованием.
II тип:
1) упражнения на составление задач по готовому чертежу, направленные на формирование геометрических понятий;
2) упражнения на составление задач по готовому чертежу, направленные на усвоение отдельной теоремы;
3) упражнения на составление задач по готовому чертежу, направленные на усвоение блока понятий и теорем.
III тип:
1) составление задач на основе анализа ситуации, заданной чертежом;
2) составление серии задач по опорному чертежу к теме;
3) составление серии задач по опорному чертежу к разделу.
Учащиеся должны уметь из многих способов деятельности при решении геометрической задачи выбрать наиболее подходящие для данной ситуации. Поэтому необходима специально организованная работа, направленная на формирование приемов деятельности по работе с чертежом задачи.
Опыт работы школы показывает, что геометрический чертеж может оказывать как развивающее, так и тормозящее влияние на достижение целей обучения геометрии в школе. Для усиления развивающего влияния чертежа и исключения его тормозящего влияния необходимо целенаправленно формировать и развивать умения оперирования с чертежом в соответствии с условием теорем, задач через систему упражнений.
Задания на составление задач по готовым чертежам позволяют не только активизировать мышление учащихся, но и способствуют развитию умения решать геометрические задачи.
Приведем пример упражнений на готовых чертежах по теме «Признаки равенства треугольников». После изучения всех трех признаков равенства треугольников учащимся предлагаются задачи, направленные на наглядное восприятие изученного и формирование целостной системы знаний по данному разделу геометрии.
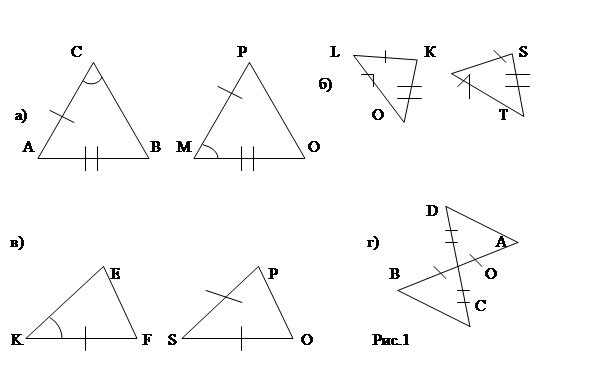
1. Пользуясь первым признаком равенства треугольников, выберите равные треугольники (рис.1).
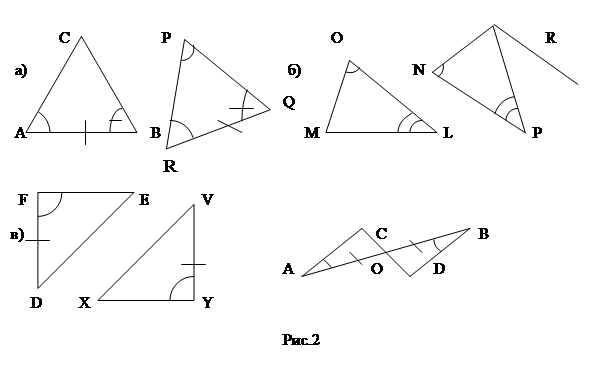
2. Пользуясь вторым признаком равенства треугольников, выберите равные треугольники (рис. 2, а-г).
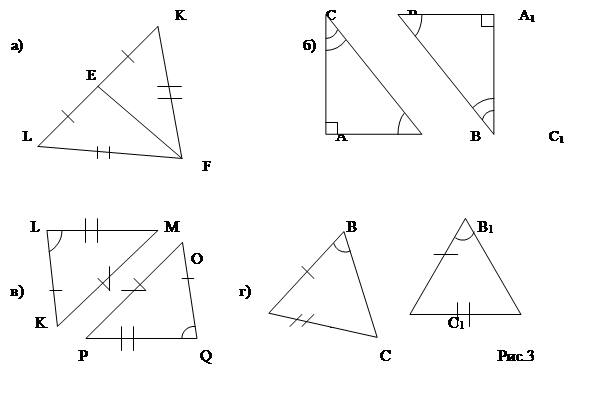
3. Пользуясь третьим признаком равенства треугольников, выберите равные треугольники (рис. 3, а-г).
4. Можно ли утверждать, что:
а) ![]() (рис.1, а); б)
(рис.1, а); б) ![]() (рис.1, б);
(рис.1, б);
г) DE=VX (рис.2, в); д) ![]() (рис.2, г);
(рис.2, г);
е) ![]() (рис.3, а); ж) AB=A1B1 (рис.3, б);
(рис.3, а); ж) AB=A1B1 (рис.3, б);
з) ![]() (рис.3, в)?
(рис.3, в)?
Как видно из данных упражнений, решение подобного рода задач не составляет особых трудностей у учащихся, так как они решаются устно. Причем умение проанализировать чертеж, четко выразить свои мысли, опираясь только на изображение, способствует активизации мышления учащихся и повышению прочности и осознанности усвоения основных понятий, фактов, методов, что в свою очередь приведет к более успешному усвоению такого сложного учебного предмета, как геометрия. Применение упражнений на готовых чертежах повышает эффективность урока и положительно воздействует на процесс формирования геометрических понятий и их образов у учащихся. Преимущество таких задач заключается также в том, что их можно применять на различных этапах урока.
Из вышесказанного можно утверждать, что применение упражнений на формирование умений работать с чертежом является очень важным методическим аспектом, т.к. задачи данного характера несут в себе, на наш взгляд, следующие функции: познавательные, развивающие и прикладные, а также функции обучения решению задач, через каждую из которых проявляется воспитывающий характер обучения. Они выполняют познавательные функции в обучении математике, т.к. в процессе их решения учащиеся приобретают математические сведения или овладевают математическими методами. Задачи выполняют развивающие функции в обучении математике, т.к. они дают возможность выработки и применения некоторых приемов логического и творческого мышления. И прикладные функции, поскольку решаются непосредственно при выполнении трудовых операций. В настоящее время основная роль задач – развитие мышления у учащихся, при этом учителей интересует сам процесс решения задачи, мыслительные операции во время решения. Поэтому при обучении решению геометрических задач одной из основных целей является: целенаправленное планомерное обучение мыслительным операциям: анализу, синтезу, сравнению и другим. А также обучение отдельным эвристическим приемам, эвристикам, позволяющим осуществить поиск решения нестандартных задач. Умение работать с чертежом в единстве с преобразованием задачи – неотъемлемая часть достижения данной цели, поэтому представленная проблема является актуальной.
Рецензенты:
Усманов В.В., д.п.н., профессор, первый проректор, проректор по научной работе,
ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.
Гарькина И.А., д.т.н., профессор, профессор кафедры «Математики и математического моделирования», ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.



